- The paper introduces EWFM which trains continuous normalizing flows to sample from unnormalized Boltzmann distributions using energy evaluations.
- It proposes iterative (iEWFM) and annealed (aEWFM) strategies to refine proposals, reduce variance, and enhance sample quality.
- Empirical results show competitive negative log-likelihoods and significantly fewer energy evaluations compared to state-of-the-art methods.
Energy-Weighted Flow Matching for Scalable Boltzmann Sampling
Introduction
The paper presents Energy-Weighted Flow Matching (EWFM), a framework for training continuous normalizing flows (CNFs) to sample from unnormalized target distributions, specifically Boltzmann distributions, using only energy function evaluations. This addresses a central challenge in scientific computing: generating independent samples from high-dimensional, multi-modal equilibrium distributions where direct sampling is infeasible and trajectory-based methods (e.g., MCMC, MD) suffer from poor mixing due to energy barriers. EWFM enables the use of expressive CNF architectures for Boltzmann sampling without requiring target samples, overcoming limitations of previous approaches that either need large datasets or are restricted to less expressive models.
Energy-Weighted Flow Matching Objective
The core innovation is the reformulation of the conditional flow matching (CFM) loss, which typically requires samples from the target distribution, into an importance-weighted objective that can be estimated using samples from an arbitrary proposal distribution. The EWFM objective leverages the known unnormalized Boltzmann density exp(−E(x)/T) and corrects for the mismatch between the proposal and target via importance weights:
LEWFM(θ;μprop)=Et,Xt,X1[EX1′∼μprop[w(X1′)]w(X1)∥utθ(Xt)−ut(Xt∣X1)∥2]
where w(x1)=exp(−E(x1)/T)/μprop(x1), and utθ is the parameterized vector field of the CNF.

Figure 1: Comparison of CFM (left, requiring target samples) and EWFM (right, using proposal samples reweighted by Boltzmann importance weights).
This formulation is mathematically equivalent to the original CFM loss under mild support conditions, ensuring that minimization yields the same optimum as if target samples were available.
Iterative and Annealed EWFM Algorithms
Iterative EWFM (iEWFM)
Direct estimation of the EWFM objective can suffer from high variance in importance weights if the proposal is far from the target. iEWFM mitigates this by iteratively refining the proposal: the current model is used as the proposal for the next training step, progressively improving overlap with the target and stabilizing gradient estimates. The algorithm employs a sample buffer to amortize the cost of CNF density evaluations and energy computations.

Figure 2: iEWFM progressively refines the proposal distribution, reducing importance weight variance and improving coverage of the target.
Annealed EWFM (aEWFM)
For highly complex energy landscapes, the initial proposal may be too poor for effective bootstrapping. aEWFM introduces temperature annealing: training begins at a high temperature (flatter landscape), gradually cooling to the target temperature. This increases the overlap between proposal and target in early stages, further stabilizing training.
Empirical Evaluation
The framework is evaluated on standard Boltzmann sampling benchmarks: GMM-40 (2D, 40-component mixture), DW-4 (8D double-well), LJ-13 (39D Lennard-Jones), and LJ-55 (165D Lennard-Jones). EWFM variants are compared to state-of-the-art energy-only methods: FAB and iDEM.
Key findings:
- Sample Quality: iEWFM and aEWFM achieve competitive or superior negative log-likelihood (NLL) and Wasserstein distance (W2) compared to iDEM and FAB, especially on high-dimensional LJ-13 and LJ-55.
- Energy Evaluation Efficiency: EWFM variants require up to three orders of magnitude fewer energy evaluations than iDEM, and are comparable to FAB, which is critical for expensive energy functions.
- Scalability: aEWFM demonstrates robust performance on the challenging LJ-55 system, indicating scalability to very high dimensions.

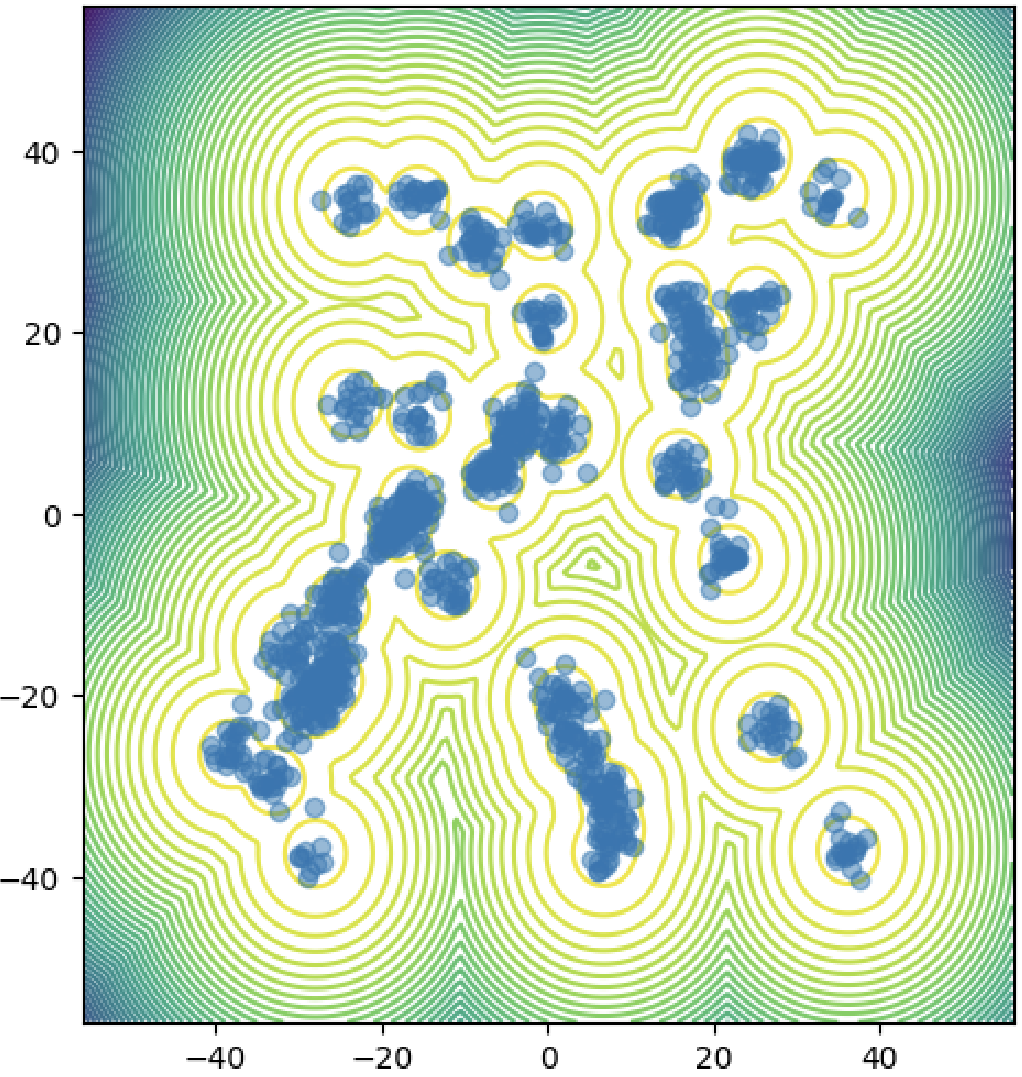
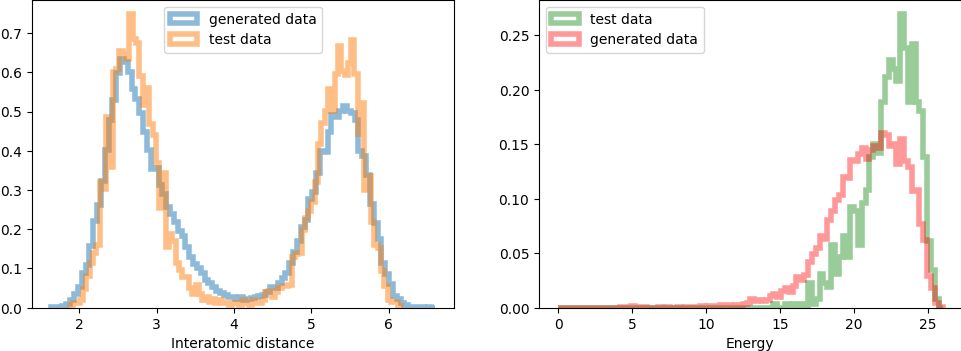
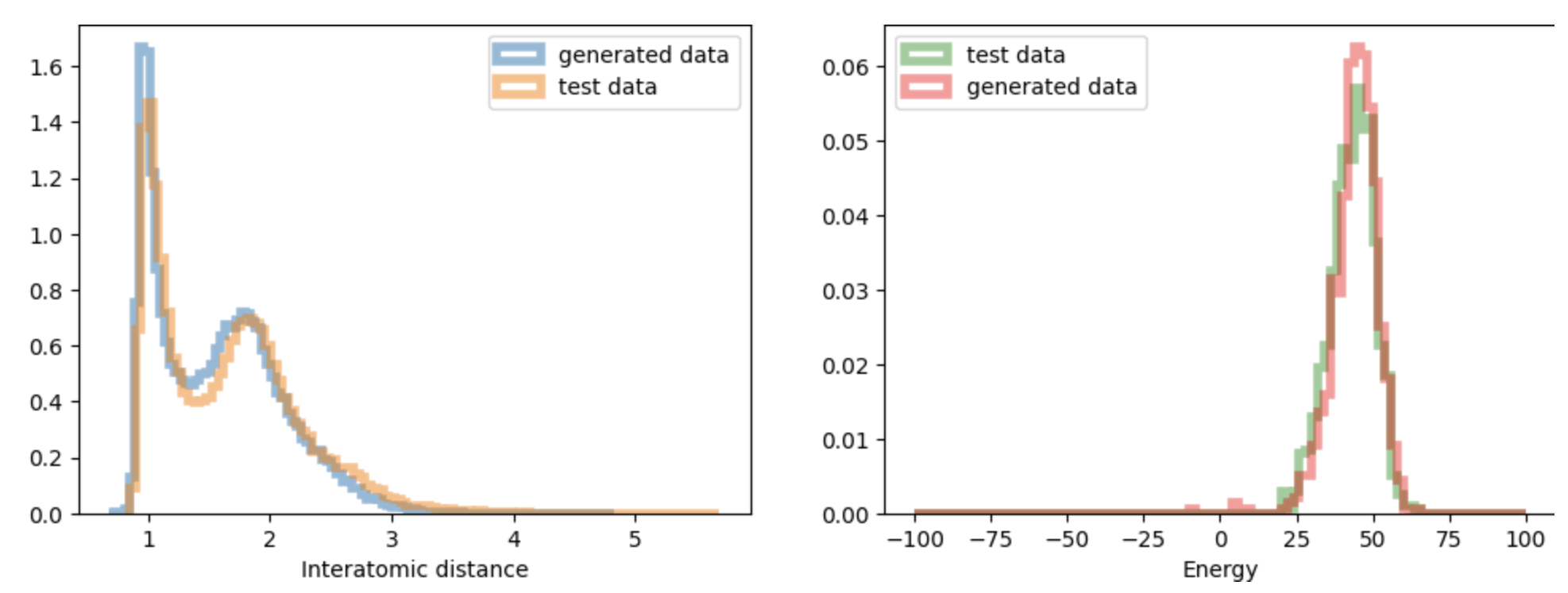
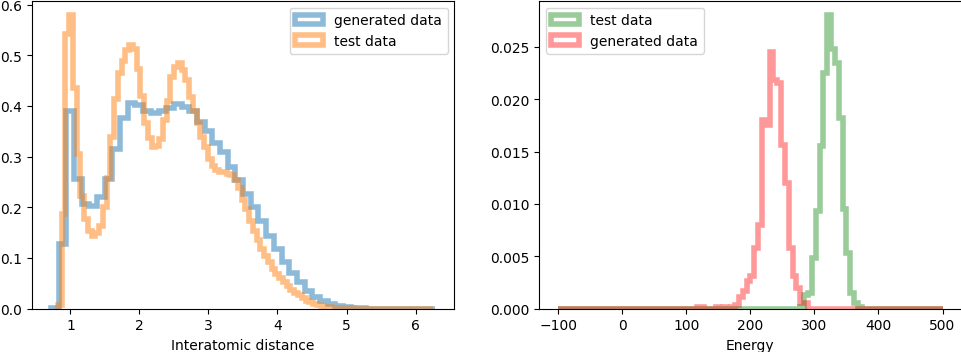
Figure 3: Qualitative sample quality across benchmarks. EWFM and aEWFM accurately capture mixture components and energy distributions, with aEWFM performing well even on LJ-55.
Theoretical and Practical Implications
The EWFM framework enables the use of CNFs for Boltzmann sampling in settings where only energy evaluations are available, unlocking the expressivity of advanced architectures for scientific applications. The iterative proposal refinement is theoretically motivated by variance reduction in self-normalized importance sampling, and the annealing strategy is justified by improved overlap in probability mass.
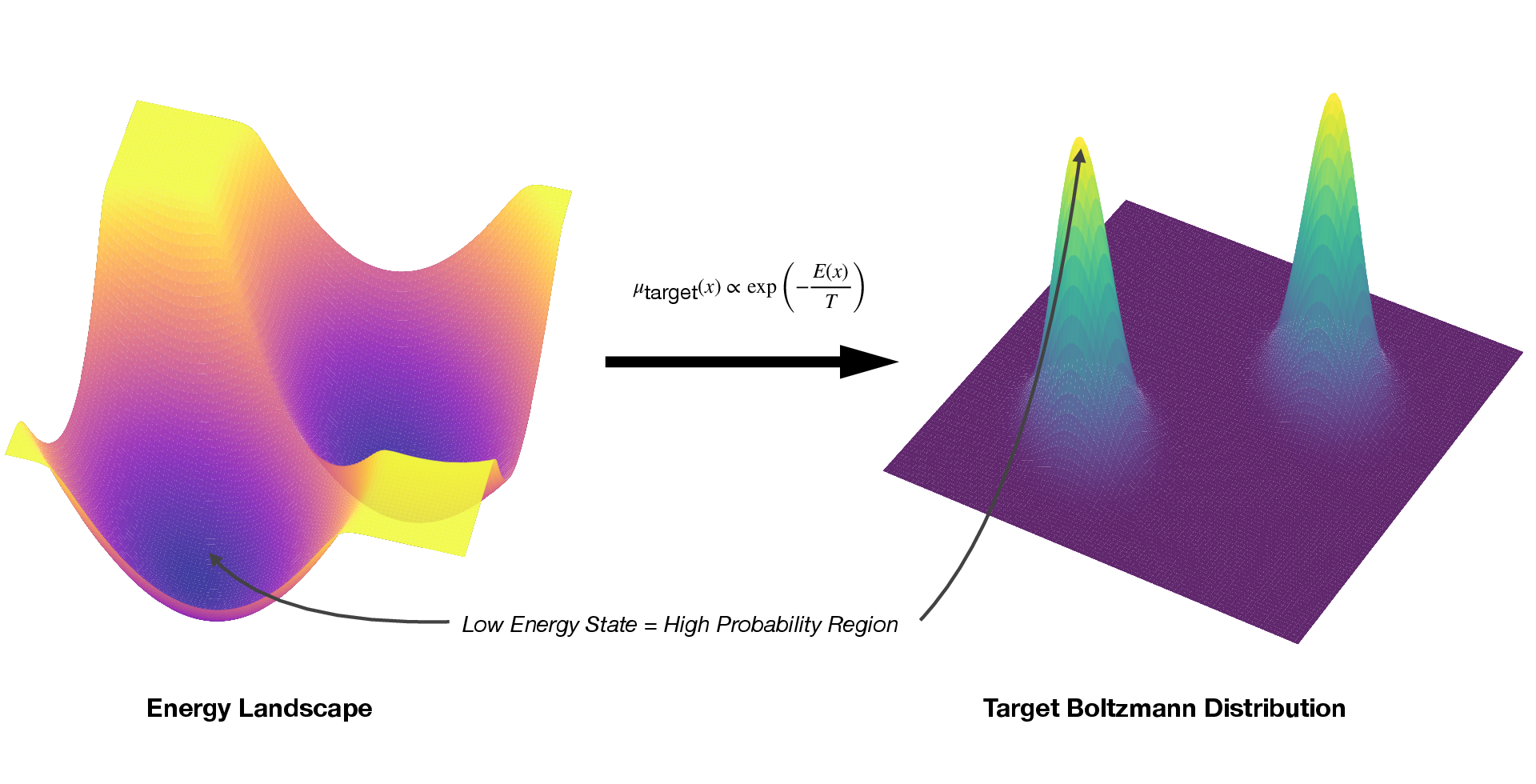
Figure 4: Boltzmann sampling problem illustrated: high-energy barriers separate low-energy regions, making direct sampling challenging.
The main trade-off is the computational cost of CNF density evaluations, which can dominate wall-clock time despite buffer amortization. This is offset by the dramatic reduction in energy evaluations, making the approach attractive for systems where energy computation is the bottleneck.
Limitations and Future Directions
- Computational Bottleneck: CNF density evaluation remains expensive; mixture model proposals or more efficient density approximations could alleviate this.
- Intermediate Complexity: On DW-4, iEWFM and aEWFM underperform compared to iDEM and FAB, possibly due to bias in gradient estimates from model proposals.
- Evaluation Metrics: Current NLL evaluation relies on training a secondary CNF; alternative metrics not requiring model retraining would be preferable.
Future work should include systematic comparison with concurrent methods (e.g., TA-BG, Adjoint Sampling), evaluation on larger molecular systems, and investigation of hybrid approaches incorporating small amounts of target data. Methodological variations such as fine-tuning versus retraining across annealing steps warrant further paper.
Conclusion
Energy-Weighted Flow Matching provides a principled, efficient, and scalable approach for training CNFs as Boltzmann generators using only energy evaluations. The iterative and annealed algorithms achieve competitive sample quality with dramatically reduced energy evaluation requirements, particularly on high-dimensional systems. The framework advances the practical applicability of generative modeling for scientific sampling tasks, with several promising directions for further optimization and extension.







