Emulation of Complex Matrix Multiplication based on the Chinese Remainder Theorem (2512.08321v1)

Abstract: Modern computing architectures feature low-precision matrix multiplication units that achieve substantially higher throughput than their high-precision counterparts. Motivated by this architectural trend, the emulation of high-precision matrix multiplication using low-precision hardware has attracted significant interest in the high-performance computing community. Ozaki, Uchino, and Imamura introduced the Ozaki-II scheme as a general framework for emulating matrix multiplication. Building on this framework, Uchino, Ozaki, and Imamura developed high-performance and power-efficient techniques for emulating single- and double-precision real matrix multiplication on INT8 matrix engines. Extending this line of research, the present study proposes high-performance emulation methods for single- and double-precision complex matrix multiplication on INT8 matrix engines, based on the Ozaki-II scheme. On an NVIDIA B200 GPU, the proposed methods achieve 4.0x--5.6x and 4.4x--6.5x speedups over the native single- and double-precision complex matrix multiplication routines from cuBLAS, respectively, for sufficiently large problem sizes. When lower accuracy than that of the standard routine is acceptable, the proposed methods can operate at even higher speed. Conversely, with only a modest increase in computation time, they can also deliver higher accuracy than the standard routines. These properties suggest that the proposed approach has the potential to serve as a default algorithm across a wide range of applications.

• The paper introduces a novel method employing the Chinese Remainder Theorem and Karatsuba algorithm to emulate high-precision complex GEMM on low-precision INT8 engines.
• It achieves 4.0–6.5× speedup over conventional FP32/FP64 routines by mapping complex arithmetic to INT8 hardware while maintaining impressive numerical accuracy.
• Analytic performance models and extensive benchmarking on NVIDIA and AMD GPUs validate the method’s efficiency and scalability for large-scale computational workloads.

Emulation of Complex Matrix Multiplication via the Chinese Remainder Theorem on INT8 Hardware

Overview

The paper "Emulation of Complex Matrix Multiplication based on the Chinese Remainder Theorem" (2512.08321) develops high-throughput algorithms for single- and double-precision complex matrix multiplication (CGEMM, ZGEMM) using INT8 matrix multiplication engines. The approach extends the Ozaki-II scheme—which previously targeted real-valued matrix products—by incorporating a Karatsuba-based formulation for complex arithmetic and modular techniques rooted in the Chinese Remainder Theorem (CRT). These methods enable the mapping of high-precision complex GEMM to architectures dominated by low-precision compute units (typically found on modern GPUs).

Numerical and performance benchmarks on NVIDIA (GH200, B200, RTX 5080) and AMD (MI300X) GPUs demonstrate that the proposed emulated GEMMs achieve 4.0×–6.5× speedup over vendor-optimized FP32/FP64 complex GEMM routines on sufficiently large problems, while also delivering greater numerical accuracy when configured accordingly.

Algorithmic Foundations and Methodology

The Ozaki-II scheme for real GEMM operates by scaling input matrices to integer form, decomposing these integers via sets of coprime moduli, performing multiple modular matrix multiplications (MMMs) using INT8 engines, and reconstructing results with the CRT. Extending to complex-valued GEMM, the scheme leverages block-structured representations for complex matrices, as well as the Karatsuba algorithm for reducing the number of required multiplications in complex products.

The conversion from floating-point to integer (including scaling and rounding) is carefully tuned for two operating modes: "fast" mode (with Cauchy-Schwarz-based bounds for scaling) and "accurate" mode (with auxiliary INT8 multiplications for tighter bounding). Both modes are parameterized by the number of moduli ($N$), with higher $N$ providing looser uniqueness conditions in CRT reconstruction, thereby ensuring precision but at increased computational cost.

The Karatsuba-based complex multiplication for $C = AB$ decomposes the task into three real MMMs, and further optimization is achieved by introducing blocking along the output dimension to mitigate degradation for large matrices.

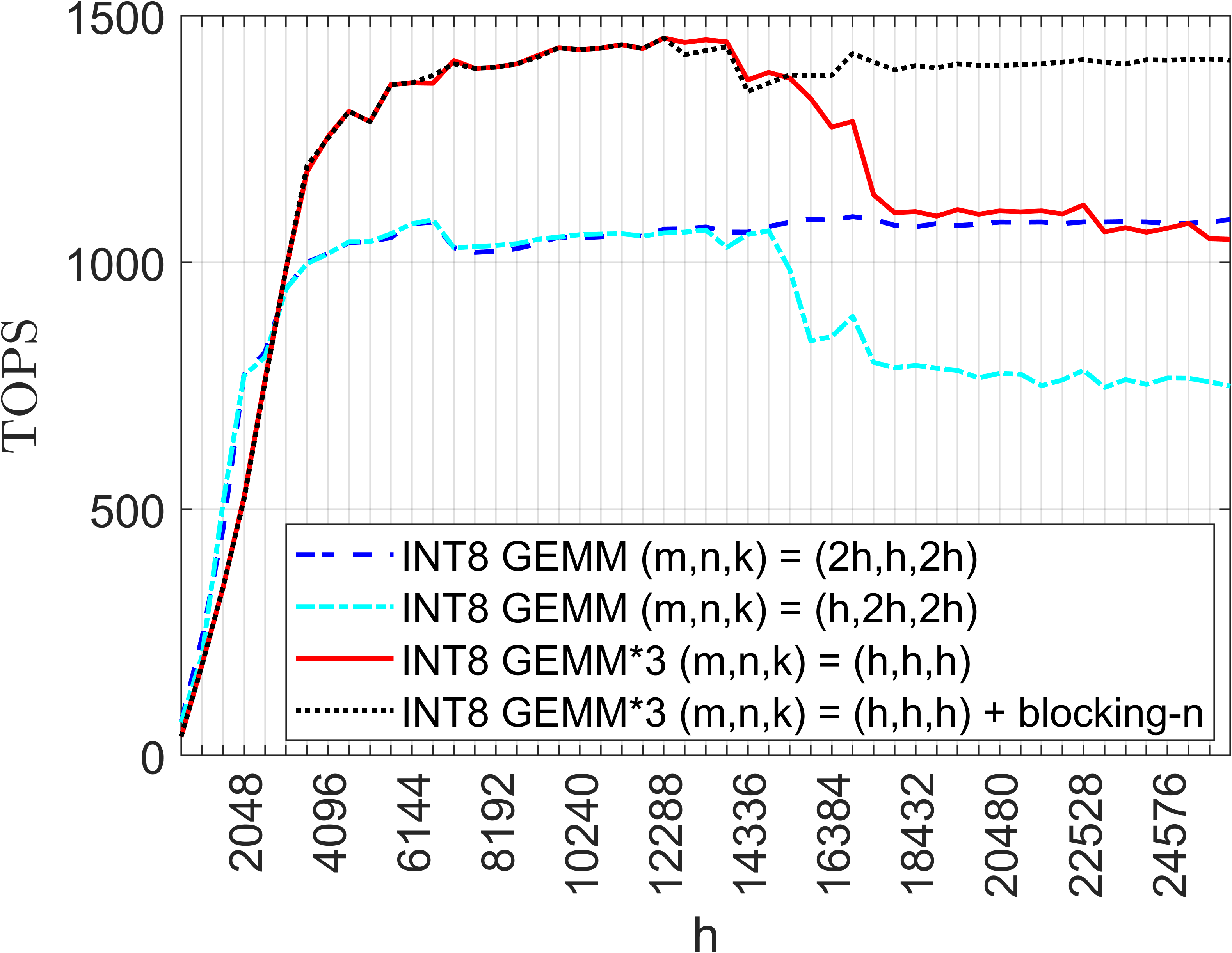
Figure 1: Comparative benchmark of four INT8-based GEMM strategies on NVIDIA H100, highlighting the efficiency gains from the Karatsuba formulation and n-blocking.

Performance Modeling

Given the pronounced hardware imbalance favoring INT8 throughput over FP32/FP64, the paper develops analytic performance models that combine memory bandwidth and compute throughput. For a matrix of dimensions $m \times k$ and $k \times n$, the predicted runtime accounts for loading/storing/scaling, number of modular MMMs, conversion/CRT overhead, and parallel arithmetic corrections, with $N$ and additional correction terms ($c$) as tunable parameters.

The models align closely with observed hardware results across architectures, with throughput (measured in TFLOPS) scaling predictably as INT8/MMM ratios dominate.

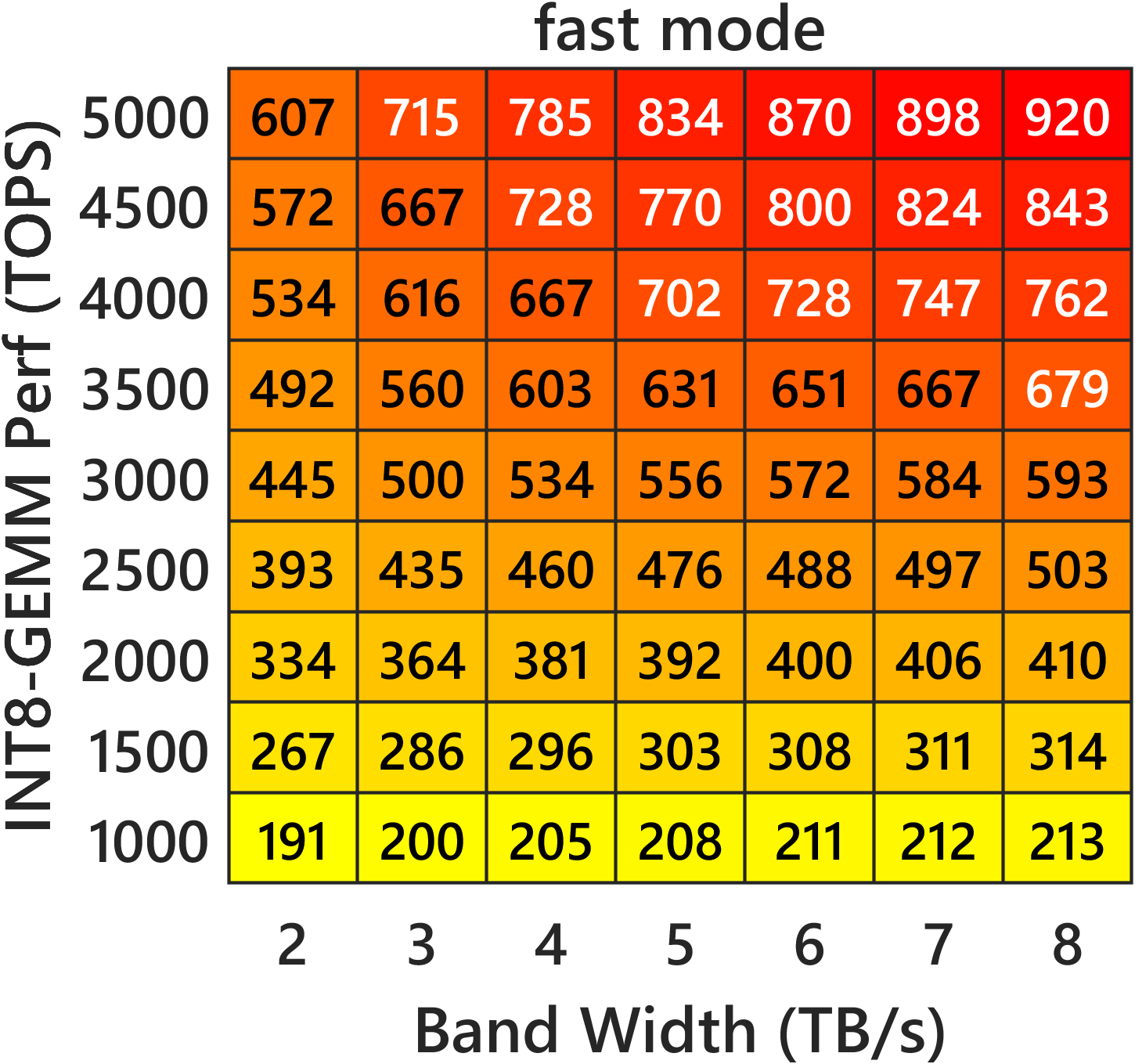
Figure 2: Heatmaps of predicted single-precision complex matrix multiplication throughput, mapping memory bandwidth and INT8 GEMM kernel performance in both "fast" and "accurate" modes.

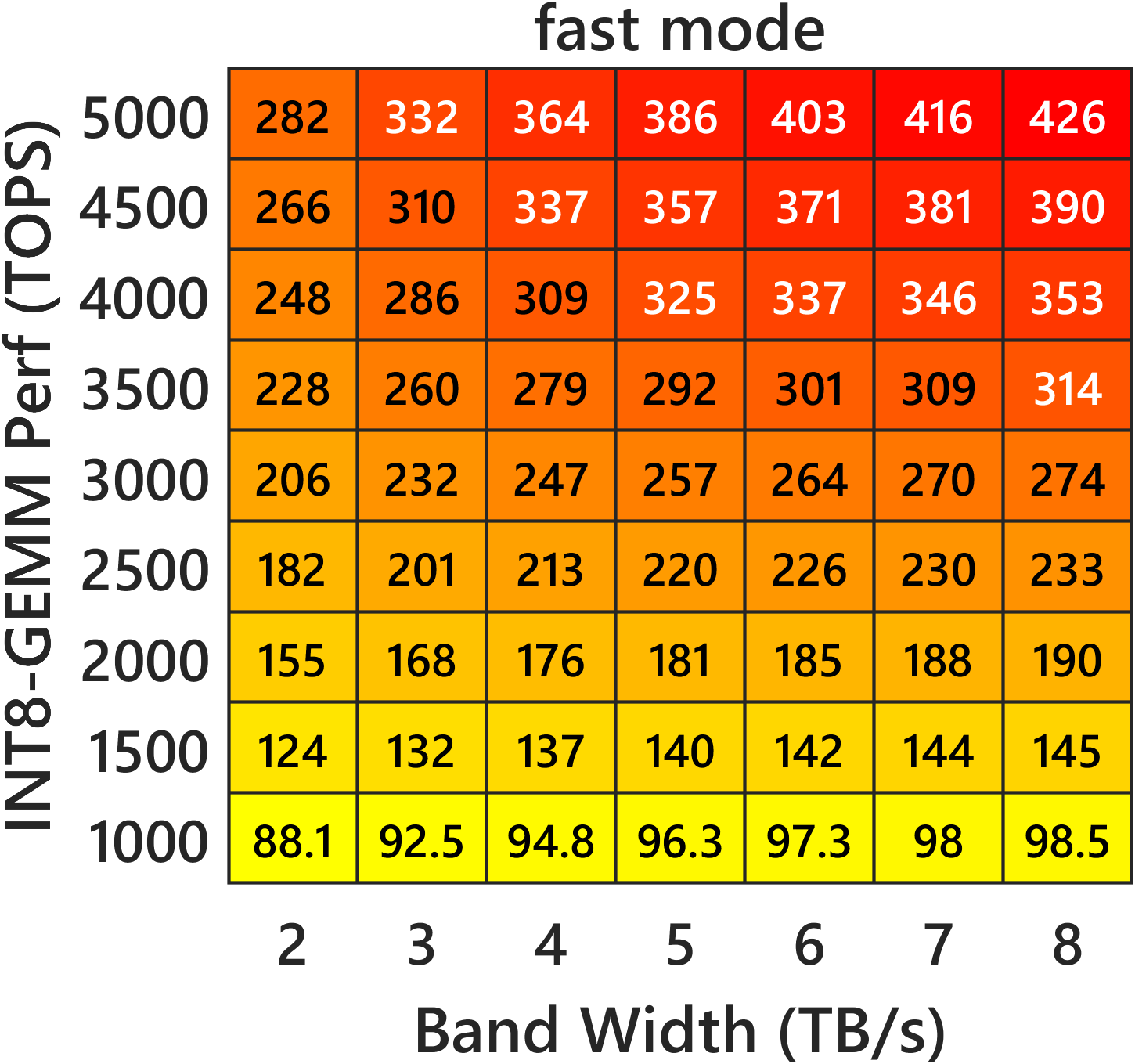
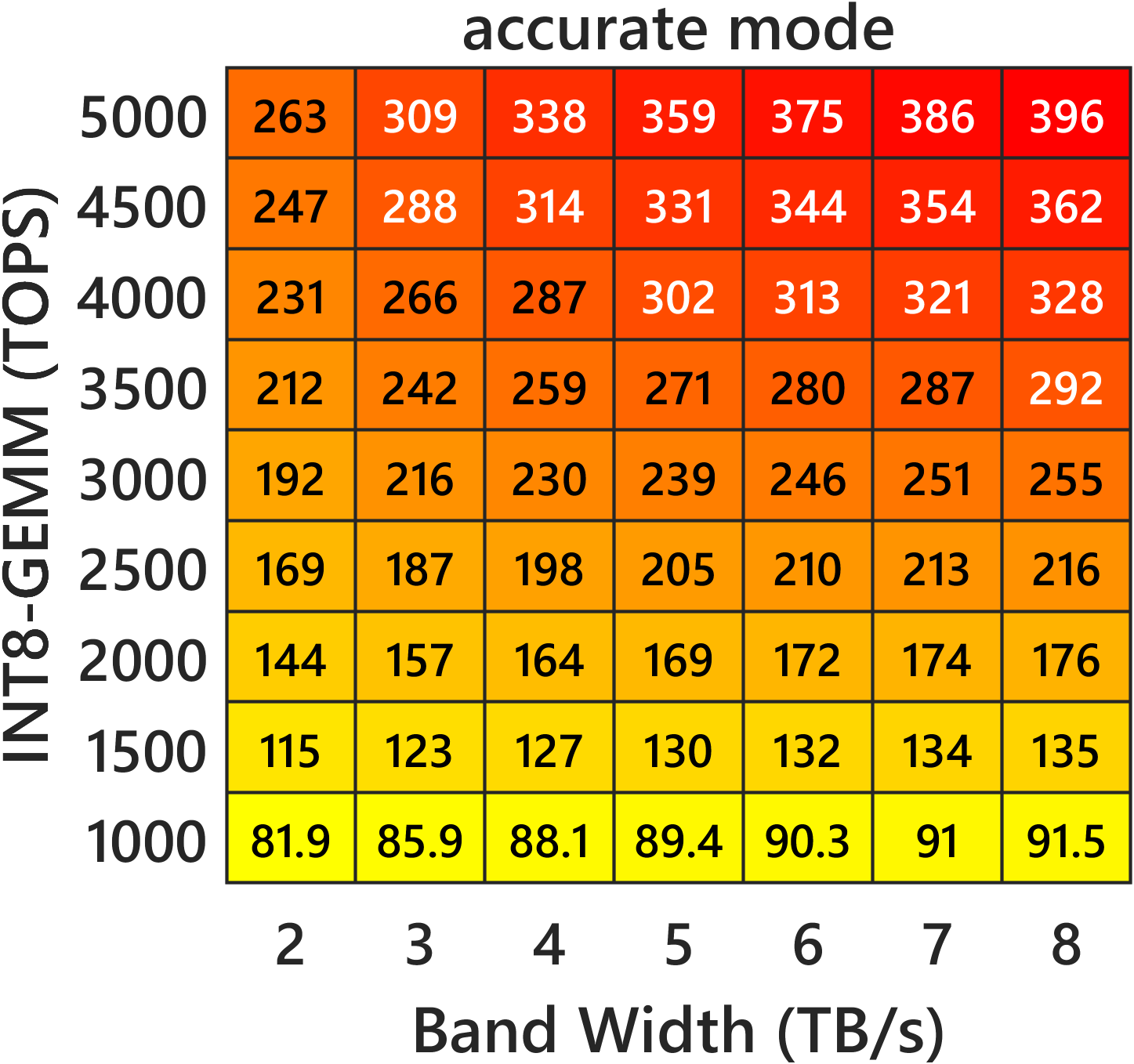
Figure 3: Heatmaps for double-precision complex emulation, illustrating throughput in TFLOPS under varying bandwidth and INT8 compute on $m=n=k=16384$ with $c=13$ moduli.

Numerical Accuracy Analysis

Randomly generated test matrices provide a comprehensive sweep across dynamic ranges, with the relative error (maximum per-component) measured against double-double reference implementations. The paper demonstrates that for CGEMM, 6–9 moduli in fast/accurate modes suffice for FP32-level accuracy, while for ZGEMM, 13–18 moduli match FP64 accuracy. The Karatsuba algorithm’s application notably reduces required moduli relative to prior DGEMM emulation [uchino_ozaki2], directly suppressing error propagation.

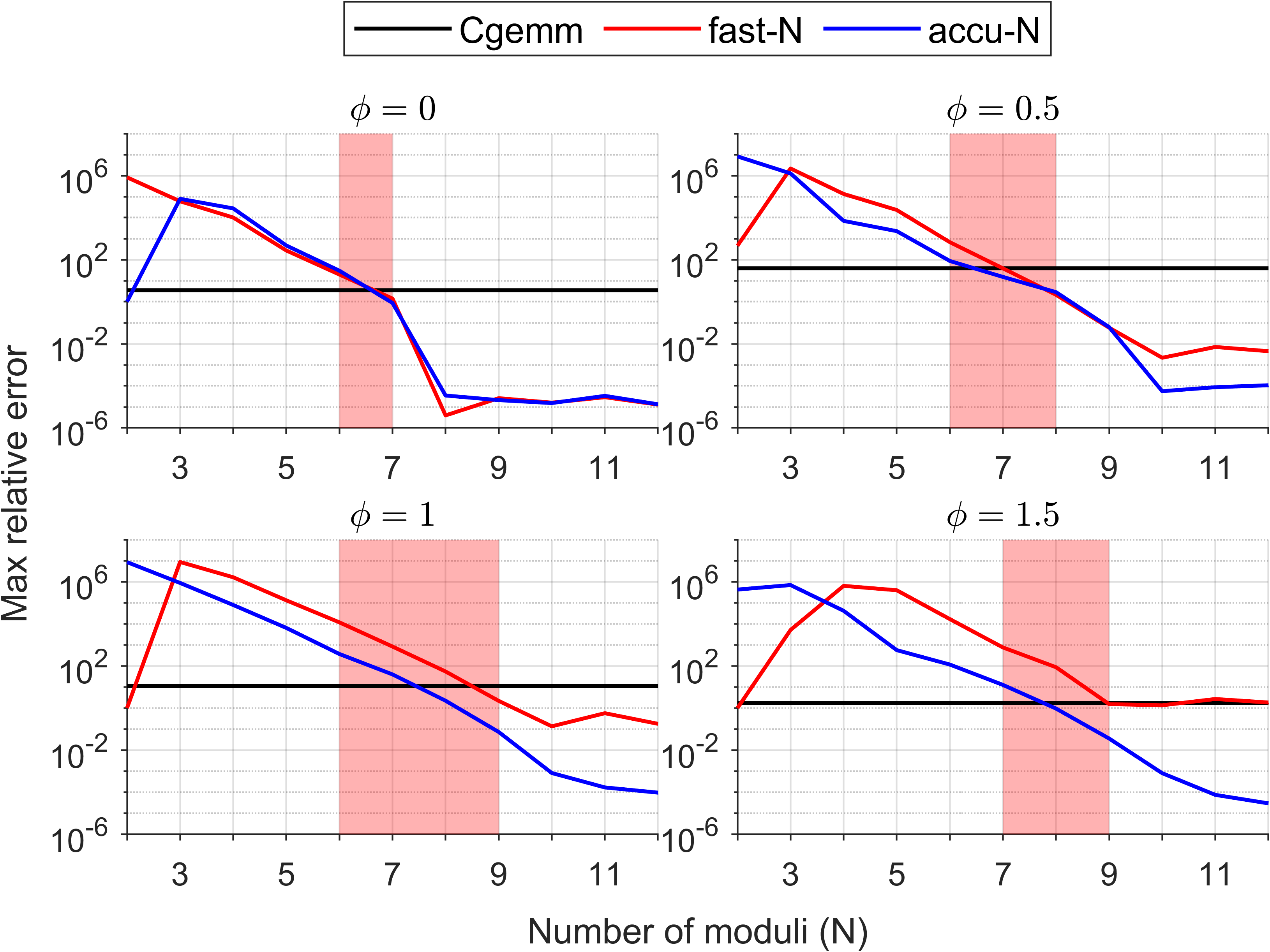
Figure 4: Maximum relative error in single-precision complex MMM on NVIDIA GH200 with $m=n=1024$ and $k=16384$.

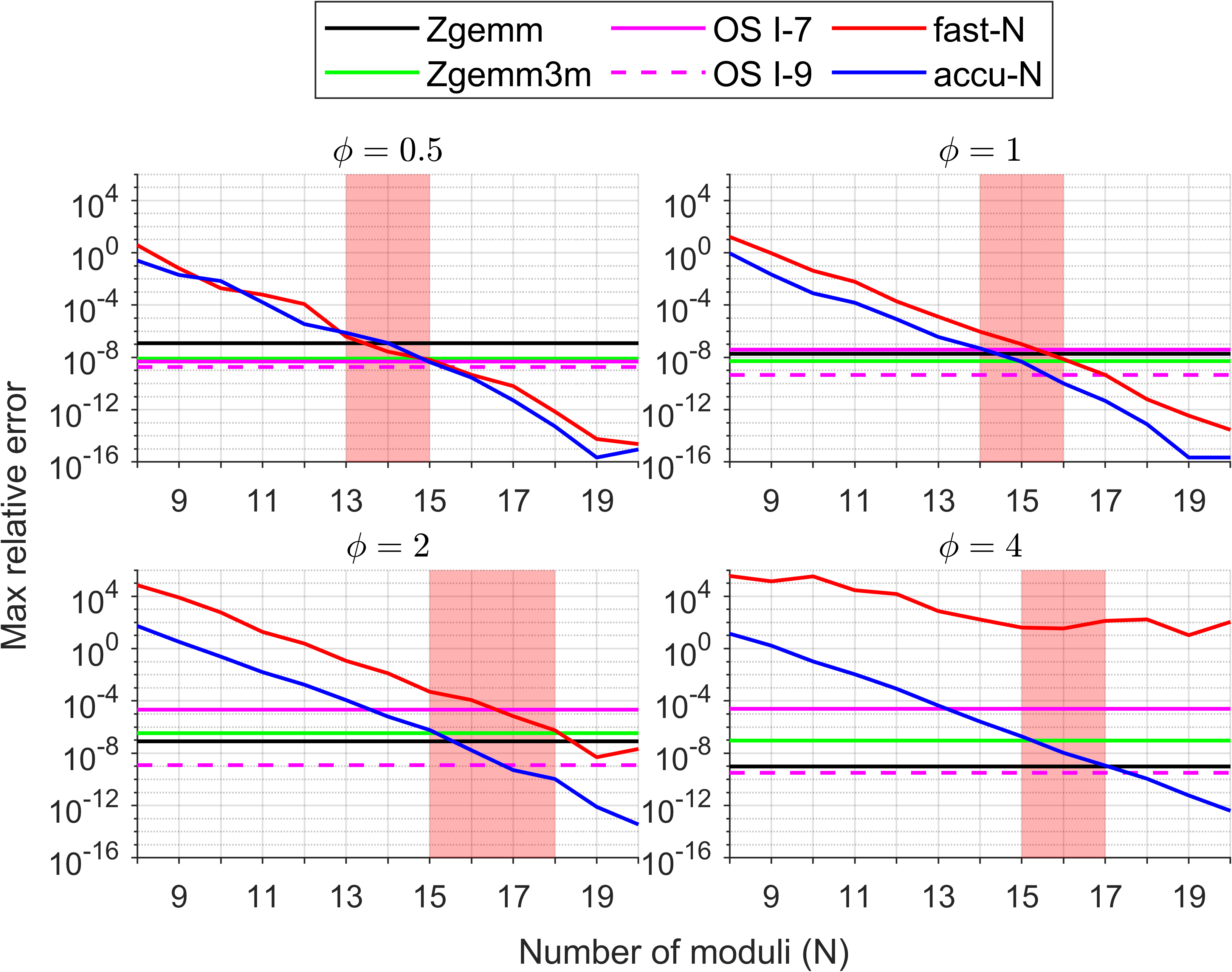
Figure 5: Maximum relative error in double-precision complex MMM under identical setup, demonstrating precision preservation for the proposed method.

Extensive Benchmarking Across Architectures

Performance profiles across various GPU platforms highlight the correlation with INT8/FP64/FP32 throughput ratios. On NVIDIA B200 and RTX 5080, speedups of 4.0×–6.5× (ZGEMM), 2.1×–3.2× (CGEMM) are realized, outperforming both cuBLAS/hipBLAS native and Ozaki-I emulated kernels in vendor libraries.

On MI300X, due to a less skewed INT8/floating-point ratio, speedups are limited (0.8×–1.6×), underscoring architectural constraints. The method consistently benefits from blocked Karatsuba multiplication, with performance improvements maintained for very large problem sizes, in contrast to prior methods.

Comparisons with Ozaki-I highlight the algorithmic advantage: Ozaki-II with $N$ moduli and Karatsuba decomposition mandates only $3N$ INT8 GEMMs (further reduced via blocking), versus $S(S+1)/2$ in Ozaki-I with $S$ slices, resulting in direct performance gains.

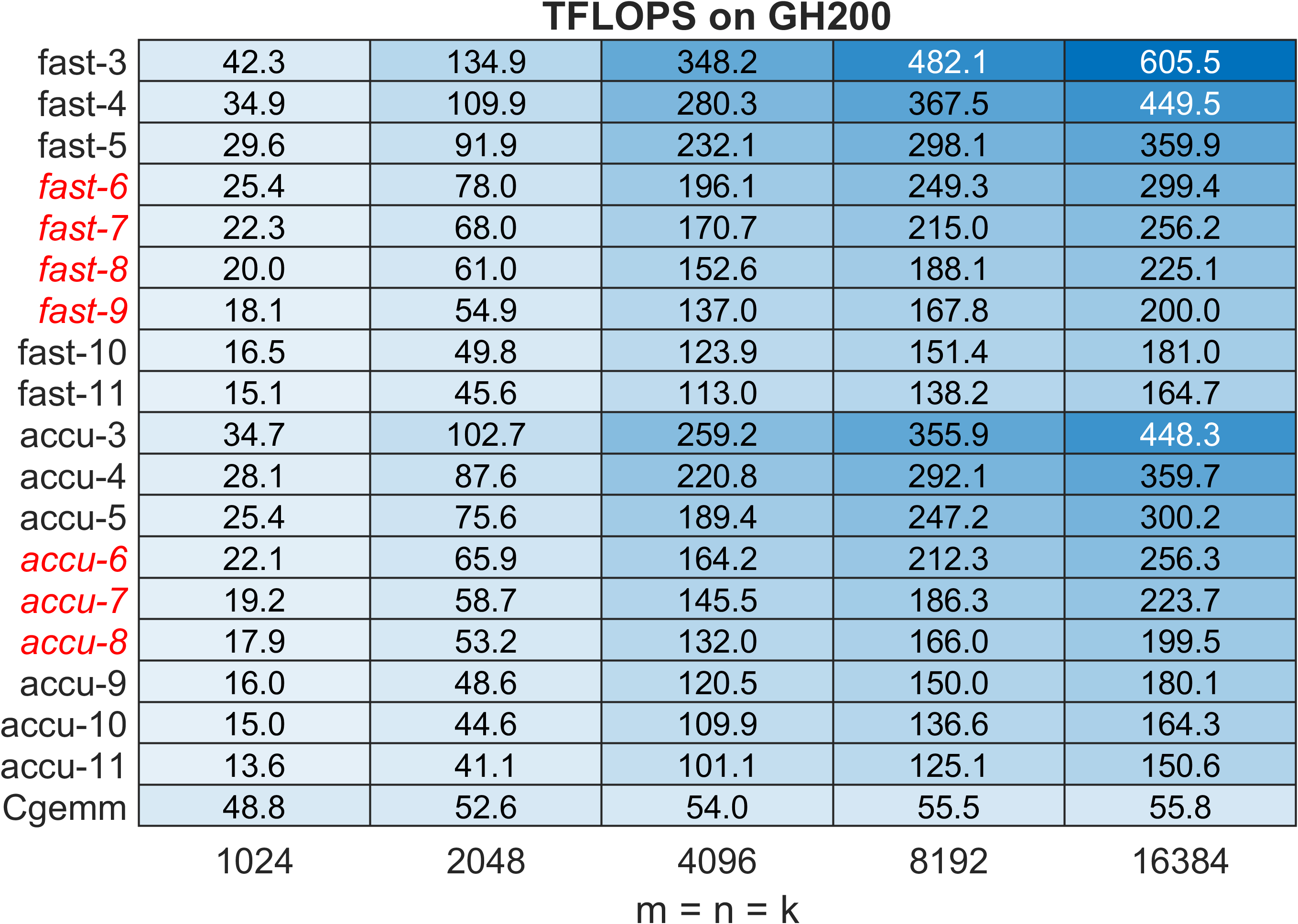
Figure 6: CGEMM TFLOPS performance on GH200; red italic traces denote Ozaki-II configurations reaching FP32-level accuracy.

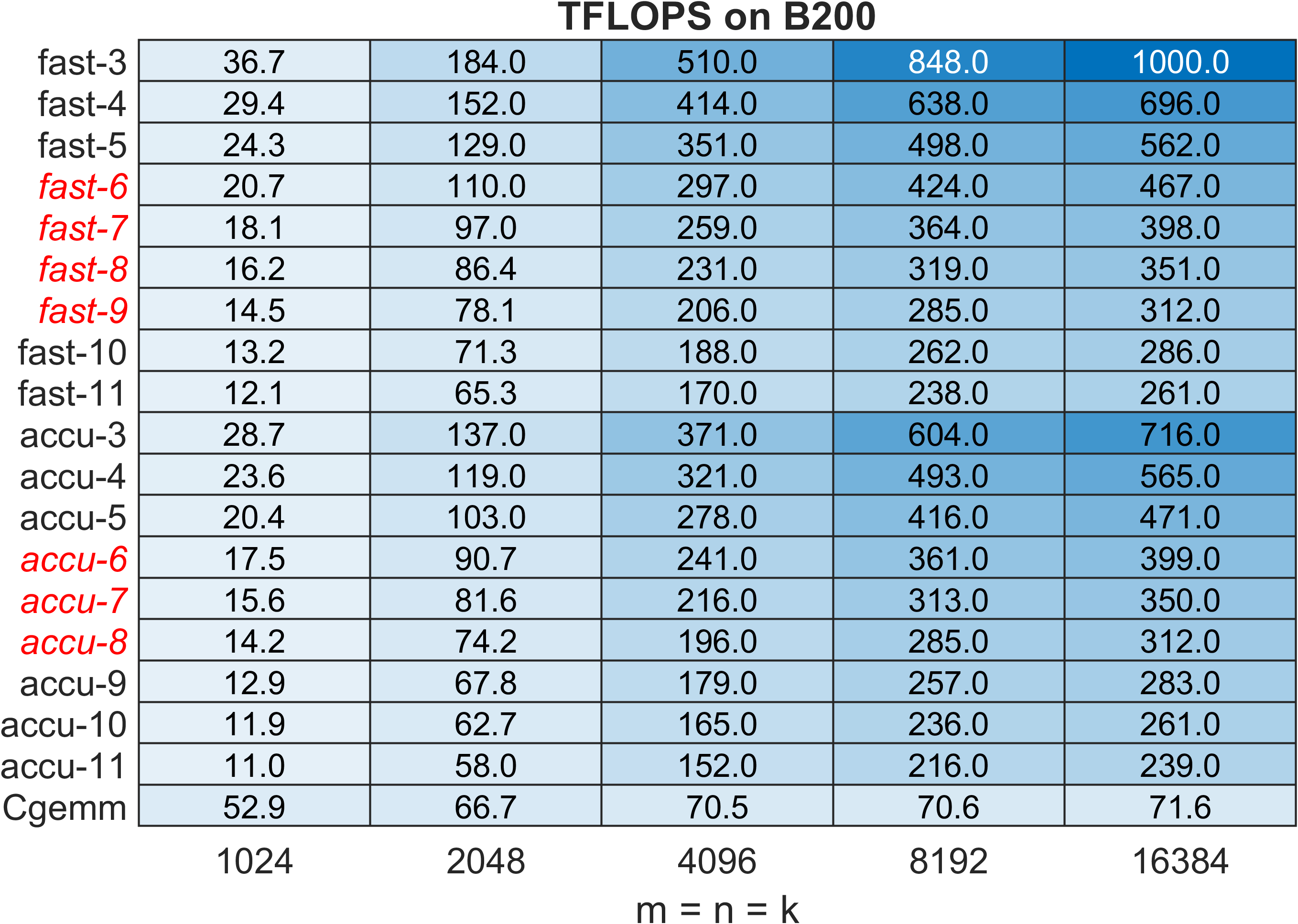
Figure 7: CGEMM TFLOPS on B200 Blackwell, further accentuating speedup trends on architectures with extreme INT8/Floating-point imbalance.

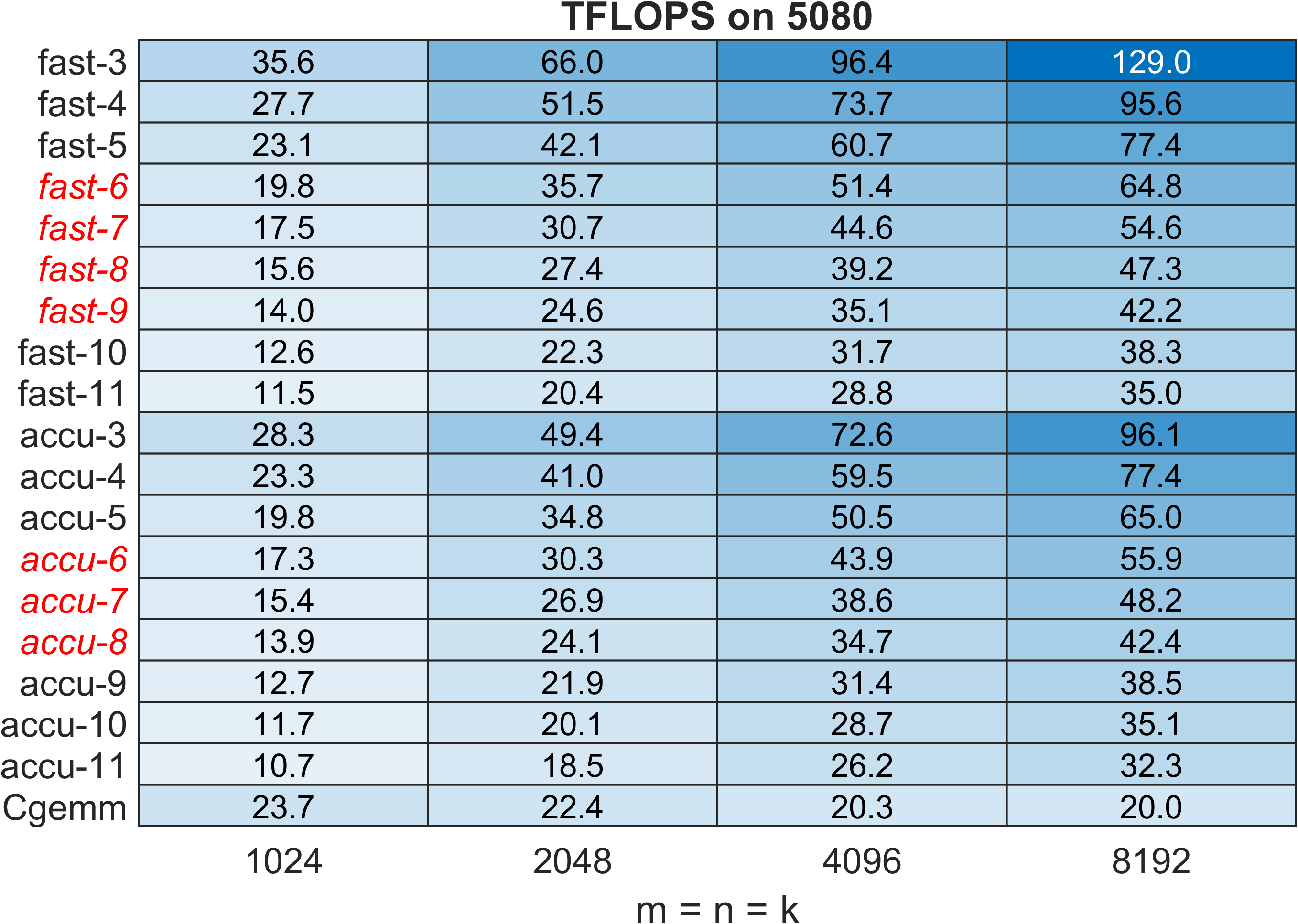
Figure 8: CGEMM TFLOPS on RTX 5080 Blackwell GPU; acceleration reflects the architecture’s highly INT8-optimized design.

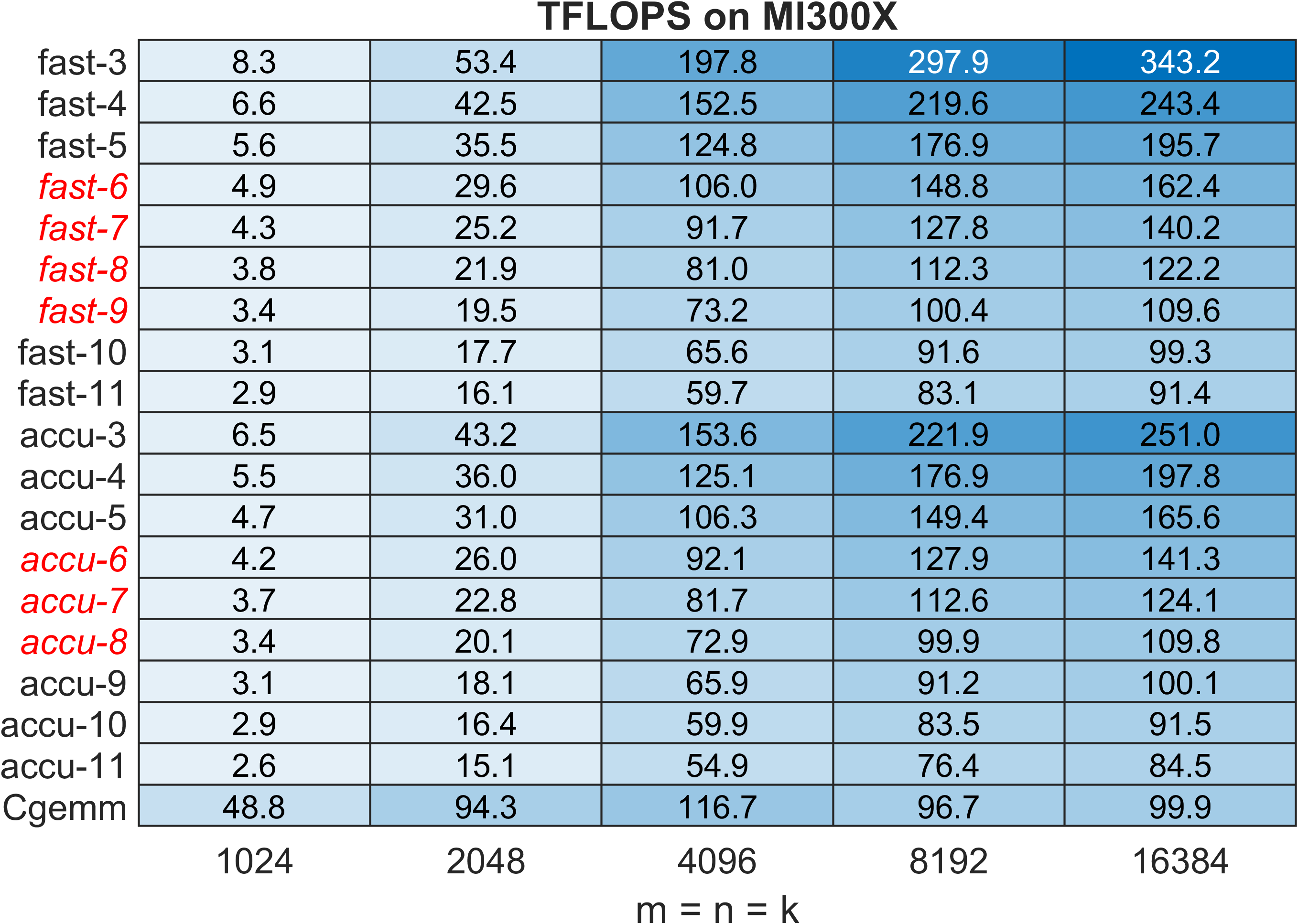
Figure 9: CGEMM TFLOPS on AMD MI300X, with speedup dampened due to lower INT8 computational dominance.

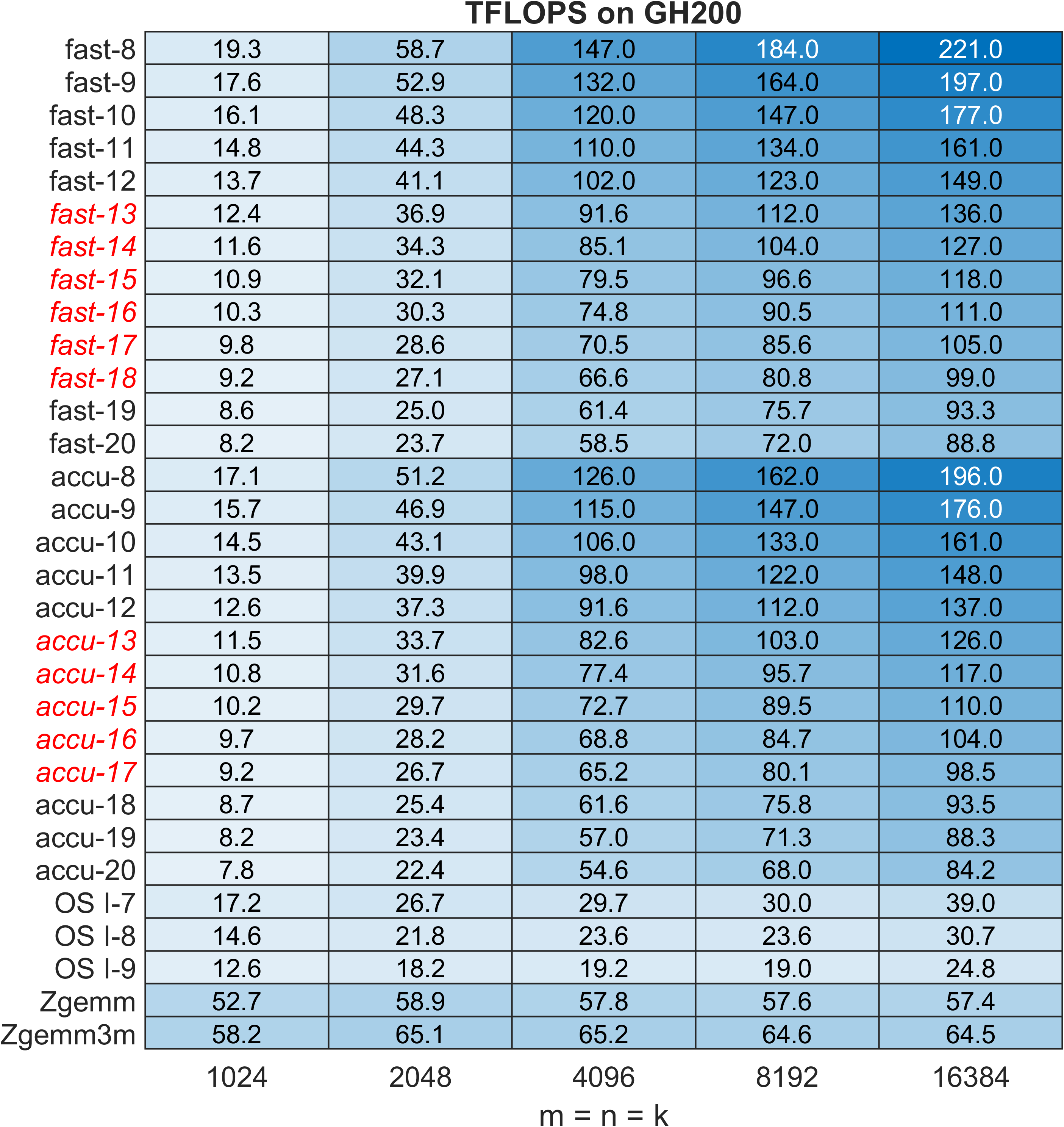
Figure 10: ZGEMM TFLOPS on GH200; red italic traces indicate Ozaki-II configurations sustaining FP64-level accuracy.

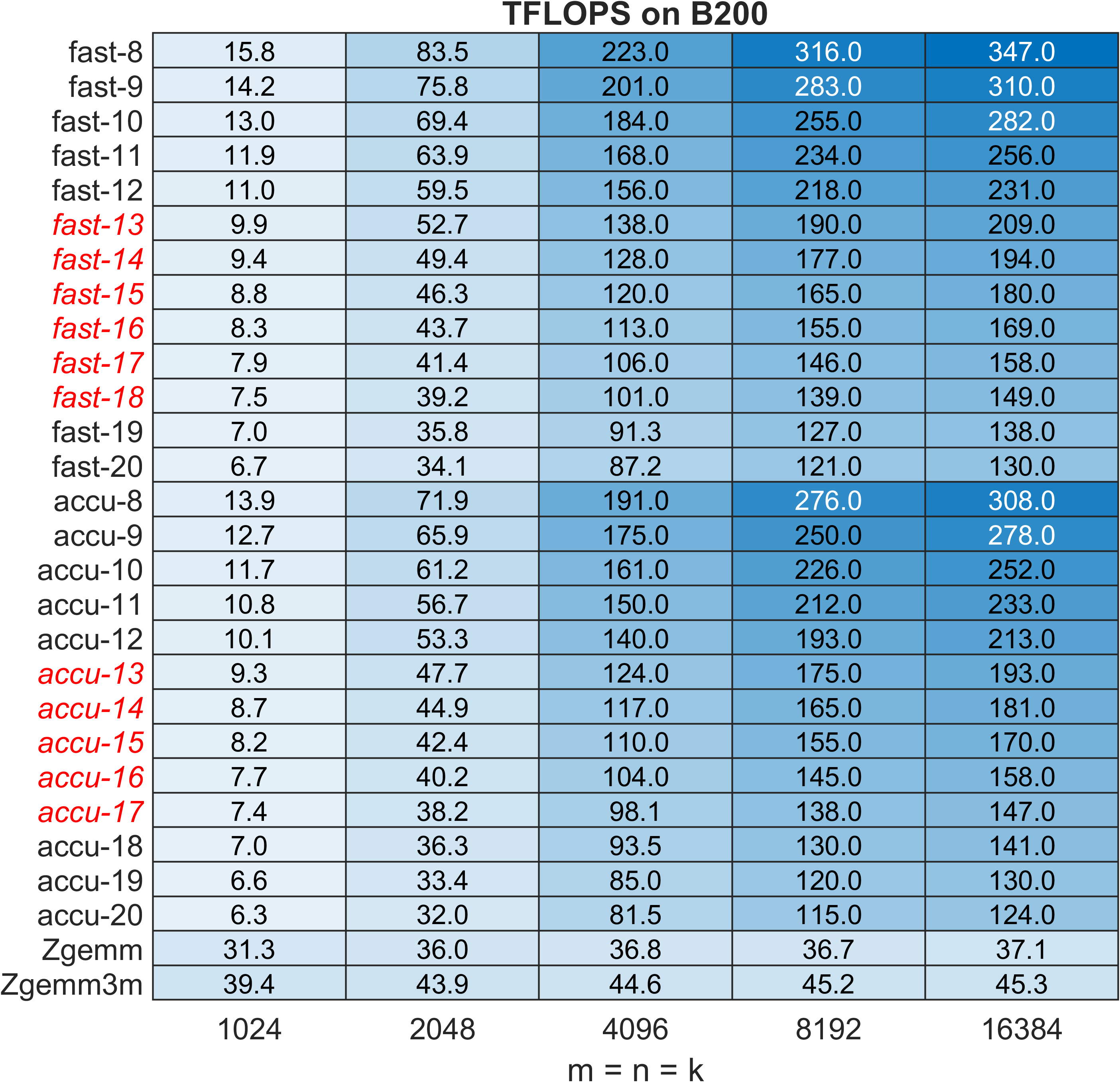
Figure 11: ZGEMM TFLOPS on B200 Blackwell; pronounced acceleration visible for large $N$ in proposed methods.

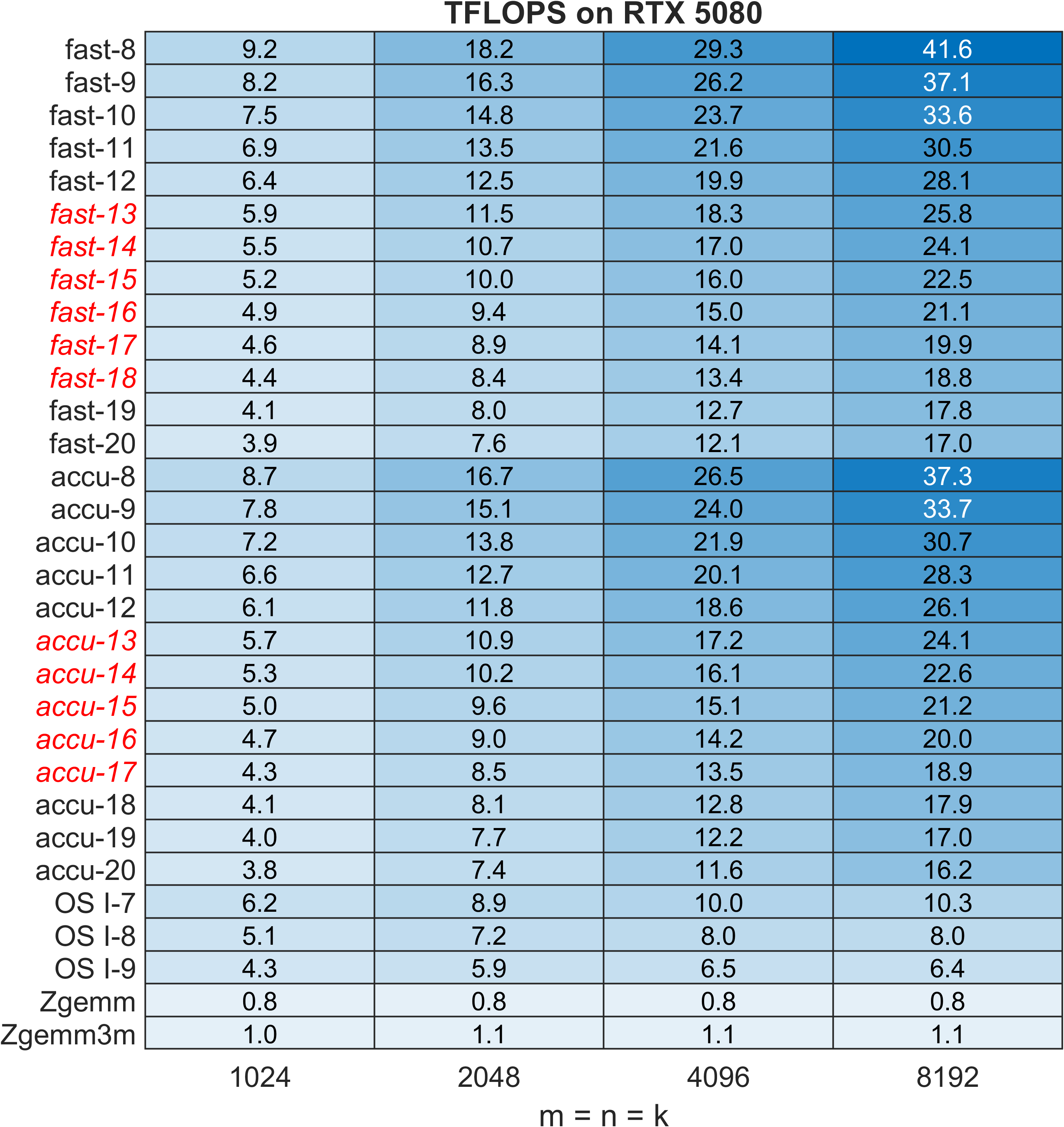
Figure 12: ZGEMM TFLOPS on RTX 5080; speedups reaching 22×–30× due to INT8 units overwhelming FP64 pipelines.

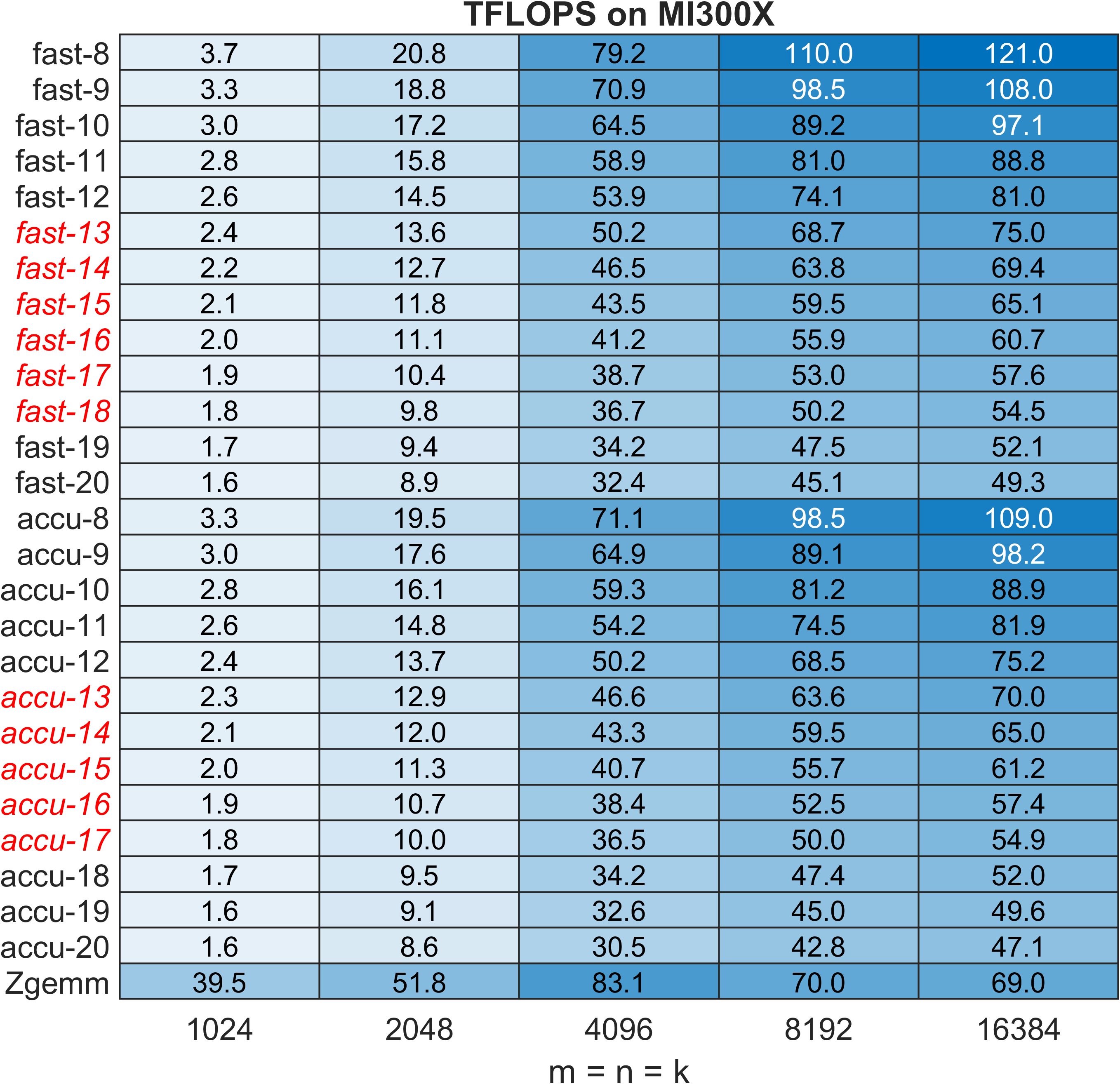
Figure 13: ZGEMM TFLOPS on AMD MI300X; near parity with native routines due to balanced hardware.

Implications and Future Directions

The low-precision emulation paradigm—demonstrated to be efficient for complex and real matrix multiplication—can be foundational for high-performance scientific computing workflows, including those in quantum simulation, PDE solvers, and computational chemistry, where complex GEMM routines often dominate runtime.

Potential future advancements include comparison and integration with BF16x9 CGEMM emulation (cuBLAS 12.9+) for B200/B300, adaptation to architectures with reduced INT8 functionality (e.g., B300), as well as further reduction in working memory requirements, which currently constitutes the principal practical limitation for large-scale deployment in memory-constrained settings.

The modular emulation approach also provides a template for extending error-free transformations and high-precision numerical methods onto new hardware platforms with alternative matrix engines (FP8, FP16, BF16), albeit with attendant limitations in accumulation precision and exponent scaling.

Conclusion

This work establishes the Ozaki-II scheme, extended with Karatsuba-based complex emulation and modular methods, as a highly performant and numerically robust approach to complex GEMM on INT8-dominated hardware. The implementation outperforms vendor-optimized and previously established emulation schemes on leading NVIDIA and AMD accelerators, with accuracy-equivalent configurations readily achievable for both single- and double-precision cases. The practical impact is significant for HPC workloads where matrix multiplication is bottlenecked, and continued refinement of memory utilization and support for emerging architectures will further cement this method’s utility in computational science and engineering.

(2512.08321)