Four Over Six: More Accurate NVFP4 Quantization with Adaptive Block Scaling (2512.02010v1)

Abstract: As LLMs have grown larger, low-precision numerical formats such as NVFP4 have become increasingly popular due to the speed and memory benefits they provide. However, to accelerate computation with NVFP4, all matrix multiplication operands--weights and activations in the forward pass, and weights, activations, and gradients in the backward pass--must be quantized to NVFP4, often leading to divergence during training and performance degradation during inference. NVFP4 by evaluating multiple potential scale factors for each block of values. To address this issue, in this work we introduce Four Over Six (4/6), a modification to the NVFP4 quantization algorithm that evaluates two potential scale factors for each block of values. Unlike integer formats, floating-point formats such as FP4 have the most quantization error on near-maximal values in each block, which we find to be primarily responsible for downstream performance degradation. We find that for some blocks, scaling to smaller FP4 values makes the distribution of representable values more uniform, improving representation of near-maximal values. Importantly, 4/6 can be implemented efficiently on NVIDIA Blackwell GPUs, making it viable to use while training LLMs with NVFP4. In pre-training experiments with transformer and hybrid model architectures, we find that 4/6 prevents divergence in several cases, bringing training loss significantly closer to BF16 compared to models trained with current state-of-the-art NVFP4 training recipes. We also find that 4/6 can be easily incorporated into many different post-training quantization methods and generally improves downstream accuracy. We hope this inspires future work in training and deploying models with NVFP4.

• The paper presents a dual-scaling NVFP4 quantization technique that adaptively selects between scaling to 4 and 6 to minimize quantization error.
• Empirical results demonstrate improved training stability and inference performance, with up to 19.9% closer perplexity to high-precision baselines.
• The method integrates with PTQ protocols and incurs minimal overhead, making it practical for efficient LLM pre-training and deployment.

Four Over Six: Adaptive Block Scaling for More Accurate NVFP4 Quantization

Introduction and Motivation

Low-precision numerical formats have become a pivotal approach for scaling LLMs, given the enormous compute and memory requirements of state-of-the-art networks. NVFP4, a 4-bit floating point format with efficient block scaling, is central to recent NVIDIA Blackwell GPU architectures, promising significant speedups. However, NVFP4 quantization consistently incurs substantial quantization errors—especially for near-maximal activations and weights—that hinder both fine-tuning and post-training quantization (PTQ), leading to training instability and inference performance degradation.

The paper introduces Four Over Six (4/6), an algorithmic augmentation to the NVFP4 quantization process. This technique adaptively selects between two scaling schemes for each quantization block, fundamentally aiming to minimize worst-case quantization error by optimizing representability of near-maximum values. The method is implemented with negligible performance overhead on Blackwell hardware, making it viable for both LLM pre-training and deployment scenarios.

Analysis of Quantization Error in NVFP4

Sources and Localization of Error

NVFP4 stores 4-bit FP4 blocks, each equipped with an FP8 E4M3 scale factor. The quantization pipeline requires both operands (weights and activations) to be in NVFP4 for all matrix multiplications. Quantization errors arise from:

• Block-level FP8 scale factor quantization (limited exponent/mantissa precision per block).
• FP4 value rounding, especially for values near the block's maximum representable value.

Empirical error analysis demonstrates that the bulk of downstream degradation comes from rounding errors at these near-maximal values, whereas scale factor error is negligible.

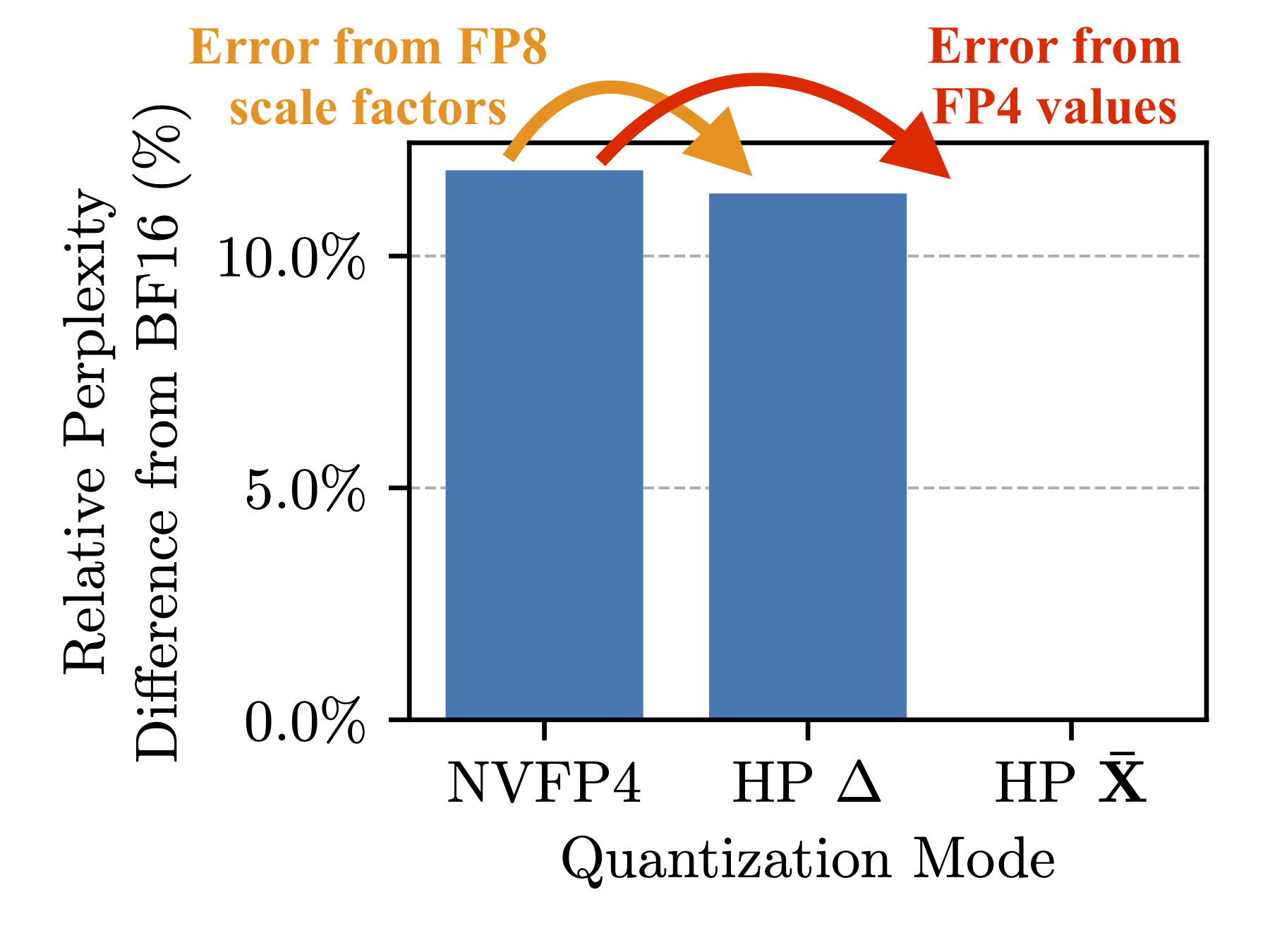
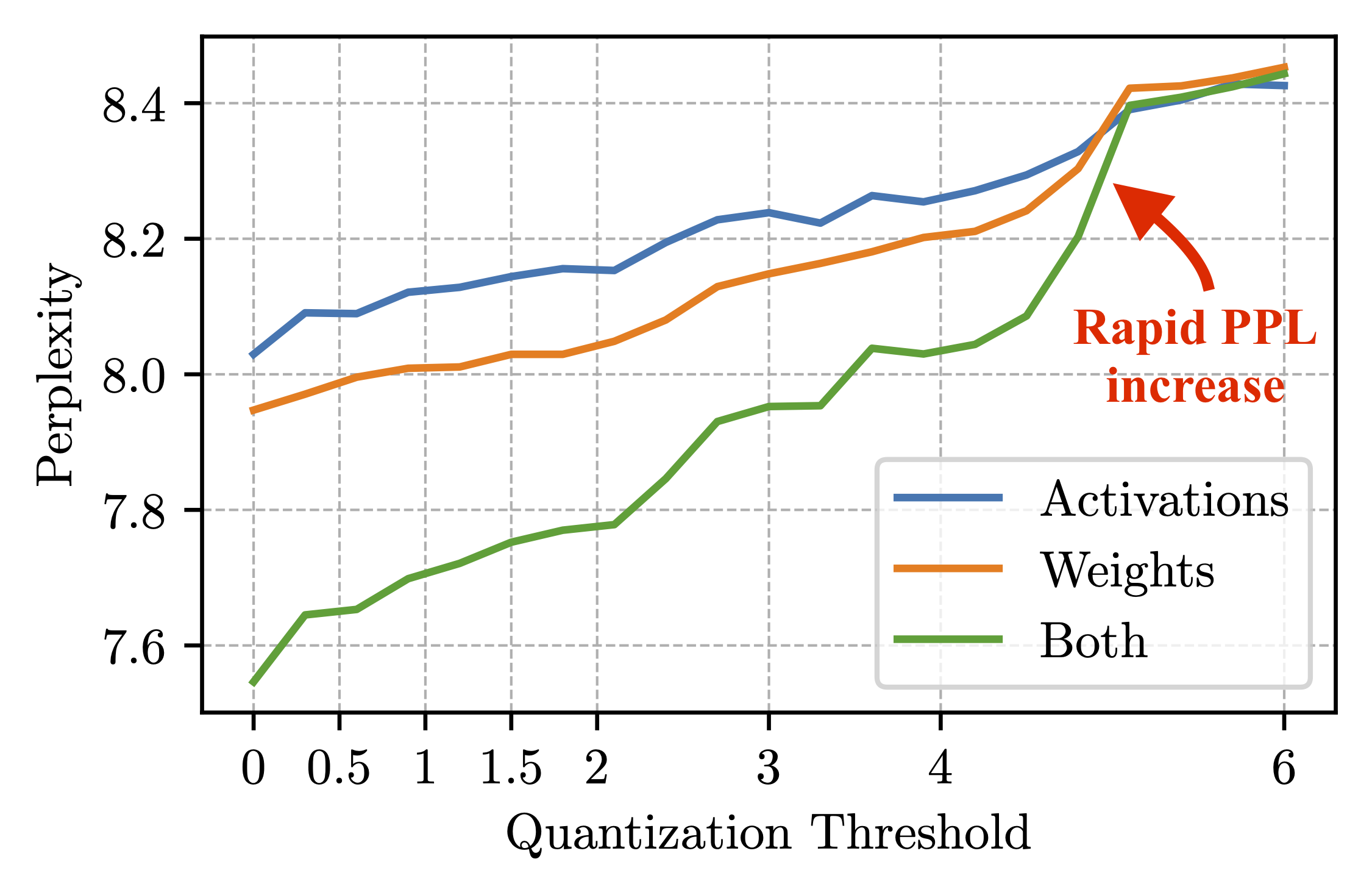
Figure 1: Quantization error due to scale factor imprecision is minimal in most scenarios; performance loss is dominated by value rounding error.

Quantizing blocks to cover the full FP4 range $[-6, 6]$ creates large steps at the upper end: the FP4 set is $\pm\{0, 0.5, 1, 1.5, 2, 3, 4, 6\}$, so values between $66.6\%$ and $100\%$ of the block maximum cannot be represented when scaling to 6. This gap leads to high, clustered quantization error precisely in the regime most consequential for deep networks.

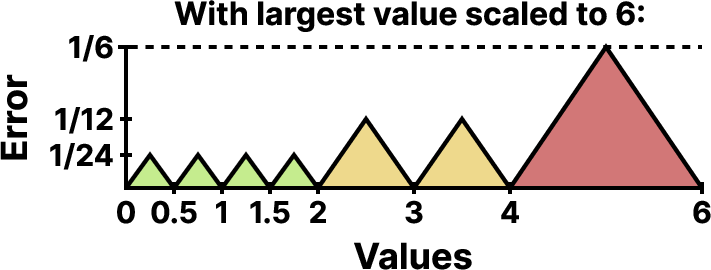
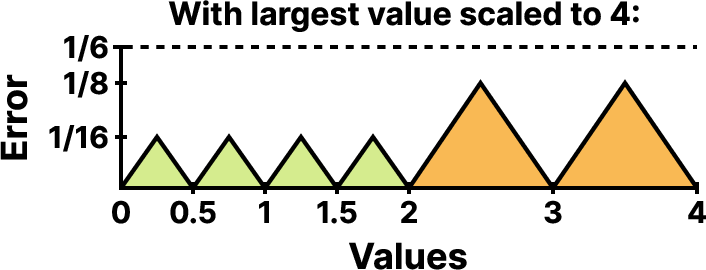
Figure 2: Quantization error relative to the largest value in a block when scaling to 6, illustrating substantial error for large-magnitude values near the maximum.

Empirical Isolation of Failure Modes

Simulation experiments, where only values above a certain threshold are quantized to NVFP4, confirm that error on values approaching the block maximum (e.g., around 5 on a scale of 6) are the principal contributors to model performance dropout.

The computational pipeline during NVFP4 training is depicted in Figure 3:

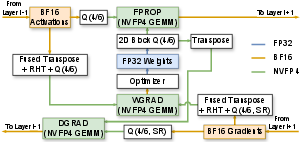
Figure 3: Dataflow of NVFP4 quantized linear layer during training under Four Over Six block scaling.

Four Over Six: Adaptive Block Scaling Algorithm

Principle and Algorithmic Details

Four Over Six (4/6) proposes to quantize each block twice: once normalized to a maximal value of 6 (full FP4 range), and once to 4, then select the scheme yielding the smallest quantization error (typically MSE). This trades the representational reach of scaling-to-6 for the finer quantization granularity of scaling-to-4, where near-maximal values (e.g., the quantized value 3 under scale 4 represents $75\%$ of the block max, and all values up to the max are more evenly mapped).

Blocks containing a spectrum of inlier and near-maximal values can thus adopt the most appropriate scaling. The inclusion criterion (select blockwise scale by MSE minimization) is empirically supported to be robust across architectures and downstream tasks.

Numerical and Hardware Efficiency Considerations

Four Over Six is engineered for runtime efficiency by utilizing CUDA/PTX instructions for packing/unpacking and error derivation within register files. Overhead is limited to $<2\%$ for inference batch sizes and $<15\%$ for large training sequence lengths, making it immediately practical for deployment.

Empirical Results and Comparisons

Mitigating Training Instability and Loss Divergence

A salient result is that Four Over Six suppresses the characteristic divergence syndrome in NVFP4 pre-training observed with previously dominant recipes. Training loss curves for transformers and hybrid architectures exhibit dramatically improved convergence profiles, closely tracking high-precision BF16 baselines.

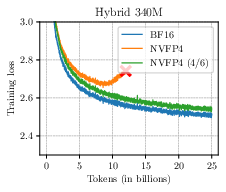
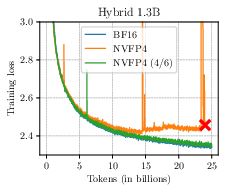
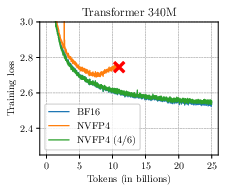
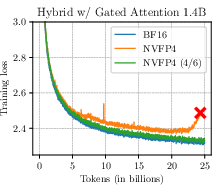
Figure 4: Four Over Six eliminates divergence during pre-training across diverse architectures and parameter scales, maintaining loss curves proximal to BF16.

Post-Training and Downstream Performance

In PTQ, integrating Four Over Six into existing quantization protocols (GPTQ, AWQ, SmoothQuant) consistently improves word perplexity and task accuracy on Llama-3 and Qwen3 series models:

• Perplexity gains: Up to 19.9% closer to reference BF16 when combined with AWQ, and 5.3% with SmoothQuant.
• Downstream task accuracy: Improvement is generally uniform or positive across multitask benchmarks.

Effects on Quantization Block Structures

The technique is particularly critical when using 2D block scales, as required for NVFP4-efficient matrix multiplications, where unaugmented NVFP4 markedly degrades accuracy (to the point of unusability) while Four Over Six restores functional performance.

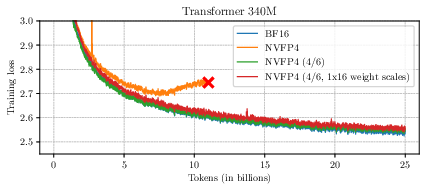
Figure 5: Training loss for Transformer (340M parameters) with and without 2D block scaling, demonstrating performance restoration using Four Over Six.

Implications, Limitations, and Future Directions

Theoretical Implications

• Localized Error Focus: The results reinforce that in block-floating formats, minimizing quantization error to in-distribution, near-maximal values trumps global error reduction strategies.
• Hardware/Algorithm Co-Design: Four Over Six is a rare example where algorithmic adaptation is purpose-built to fit emerging hardware constraints (fixed block sizes, FP8 scaling) and leverages their structure.

Practical Implications

• Training LLMs with Full Low-Precision: Four Over Six makes it feasible to train and deploy LLMs using full-path NVFP4 quantization on supported hardware, thus realizing the theoretical throughput/efficiency gains without catastrophic accuracy loss or divergence.
• Drop-in Enhancement for PTQ: The method is modular and can be integrated into PTQ pipelines for additional performance gains without substantial overhead.

Limitations

• Format Dependency: 4/6 relies on available scale factor precision (FP8 E4M3) and is not directly applicable to MXFP4-style formats with coarser scale granularity (e.g., E8M0).
• Block Size/Hardware Constraints: Benefits may diminish as scale factor or FP4 precision increases, or if dynamic/adaptive block sizes are used.

Future Research

• Optimization Beyond 4/6: Extending the adaptive scaling principle to alternate floating formats, or expanding to more than two candidate scales, could further lower error.
• Hybrid Quantization: Exploring integration with emerging rotation-based PTQ methods, and outlier-regularized architectures, may yield further reduction in quantization-induced generalization gap.
• Extensive Scaling: Validating the approach on >10B parameter models, and in fine-tuning or domain adaptation scenarios, remains an open avenue.

Conclusion

Four Over Six constitutes an algorithmically straightforward but empirically effective mitigation to NVFP4 quantization error, particularly targeting the representational limitations around near-maximal values in each block. By adaptively selecting block scaling, it demonstrably rescues both training stability and inference accuracy at negligible hardware overhead on recent NV hardware. Its integration with existing PTQ frameworks and clear extensibility to broader quantization format/hardware co-design underlines its immediate and lasting impact on scalable LLM deployment and training.