Pretraining Large Language Models with NVFP4 (2509.25149v1)

Abstract: LLMs today are powerful problem solvers across many domains, and they continue to get stronger as they scale in model size, training set size, and training set quality, as shown by extensive research and experimentation across the industry. Training a frontier model today requires on the order of tens to hundreds of yottaflops, which is a massive investment of time, compute, and energy. Improving pretraining efficiency is therefore essential to enable the next generation of even more capable LLMs. While 8-bit floating point (FP8) training is now widely adopted, transitioning to even narrower precision, such as 4-bit floating point (FP4), could unlock additional improvements in computational speed and resource utilization. However, quantization at this level poses challenges to training stability, convergence, and implementation, notably for large-scale models trained on long token horizons. In this study, we introduce a novel approach for stable and accurate training of LLMs using the NVFP4 format. Our method integrates Random Hadamard transforms (RHT) to bound block-level outliers, employs a two-dimensional quantization scheme for consistent representations across both the forward and backward passes, utilizes stochastic rounding for unbiased gradient estimation, and incorporates selective high-precision layers. We validate our approach by training a 12-billion-parameter model on 10 trillion tokens -- the longest publicly documented training run in 4-bit precision to date. Our results show that the model trained with our NVFP4-based pretraining technique achieves training loss and downstream task accuracies comparable to an FP8 baseline. These findings highlight that NVFP4, when combined with our training approach, represents a major step forward in narrow-precision LLM training algorithms.

• The paper demonstrates that NVFP4 enables stable pretraining of a 12B-parameter transformer on 10T tokens with a relative error below 1.5% compared to FP8.
• It introduces robust techniques such as Random Hadamard Transforms, 2D block scaling, and stochastic rounding to mitigate quantization error and maintain training stability.
• Comparative experiments highlight NVFP4's efficiency advantages over MXFP4, reducing compute, memory, and energy requirements while preserving downstream accuracy.

Pretraining LLMs with NVFP4: Methodology, Results, and Implications

Introduction

This technical report presents a comprehensive paper of pretraining LLMs using NVFP4, a novel 4-bit floating point format designed for efficient and accurate training at scale. The work addresses the challenges of extreme quantization—specifically, the stability and convergence issues that arise when moving from 8-bit (FP8) to 4-bit (FP4) precision. The authors introduce a suite of algorithmic techniques, including Random Hadamard transforms, two-dimensional block scaling, stochastic rounding, and selective high-precision layers, to enable stable training of billion-parameter models over multi-trillion-token horizons. The methodology is validated by training a 12B-parameter hybrid Mamba-Transformer model on 10T tokens, achieving loss and downstream accuracy metrics nearly indistinguishable from FP8 baselines.

NVFP4 Format and Hardware Support

NVFP4 extends the microscaling paradigm by reducing block size from 32 to 16 elements and employing a more precise E4M3 block scale factor, combined with a global FP32 tensor-level scale. This two-level scaling approach allows for finer dynamic range adaptation and minimizes quantization error, especially for outlier values. Unlike MXFP4, which uses power-of-two scale factors and larger blocks, NVFP4's design ensures that a significant fraction of values in each block are encoded at near-FP8 precision, with the remainder in FP4.

NVIDIA Blackwell GPUs natively support NVFP4 GEMMs, delivering 2–3× higher math throughput and halved memory usage compared to FP8. The hardware also provides native stochastic rounding and efficient scale factor handling, making NVFP4 practical for large-scale LLM training.

Training Methodology

The NVFP4 training pipeline integrates several critical components:

1. Mixed Precision Layers: Approximately 15% of linear layers, primarily at the end of the network, are retained in BF16 to preserve numerical stability. All other linear layers are quantized to NVFP4.
2. Random Hadamard Transforms (RHT): Applied to Wgrad inputs in GEMMs, RHT disperses block-level outliers, mitigating their impact on quantization and improving convergence.
3. Two-Dimensional (2D) Block Scaling: Weights are scaled in $16 \times 16$ blocks to ensure consistent quantization across forward and backward passes, preserving the chain rule and reducing gradient mismatch.
4. Stochastic Rounding: Gradients are quantized using stochastic rounding, which eliminates bias introduced by deterministic rounding and is essential for stable convergence in large models.

Ablation studies confirm that omitting any of these components leads to degraded convergence or outright divergence, especially in models trained over long token horizons.

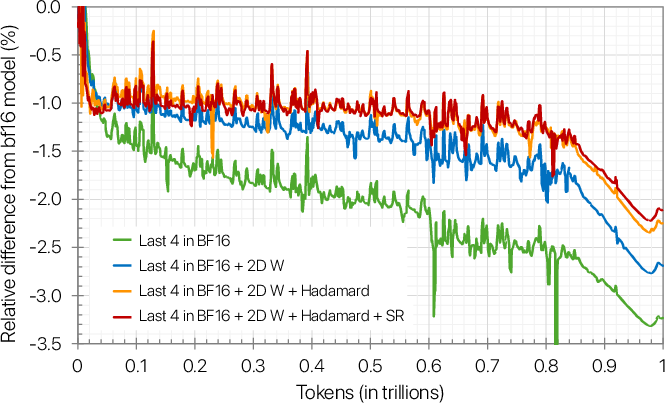
Figure 1: Combining NVFP4 training techniques yields improved validation loss for a 1.2B model, demonstrating the necessity of each component for stable FP4 training.

Empirical Results

12B Model Pretraining

A 12B hybrid Mamba-Transformer model was pretrained on 10T tokens using NVFP4 and compared to an FP8 baseline. The validation loss curve for NVFP4 closely tracks FP8 throughout training, with a relative error consistently below 1% during the stable phase and only slightly exceeding 1.5% during learning rate decay.

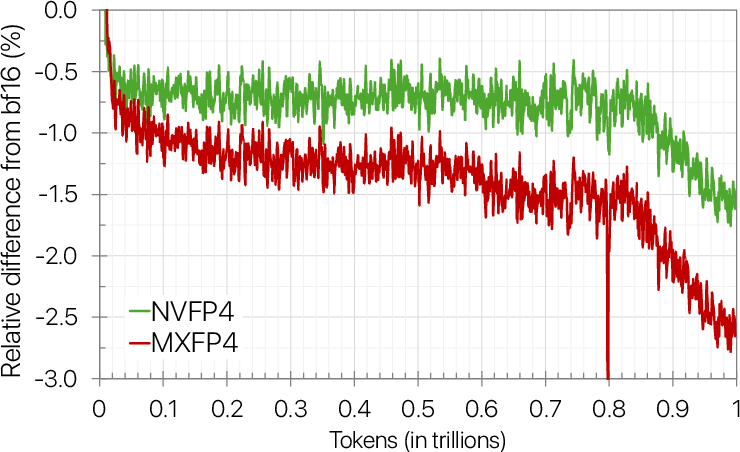
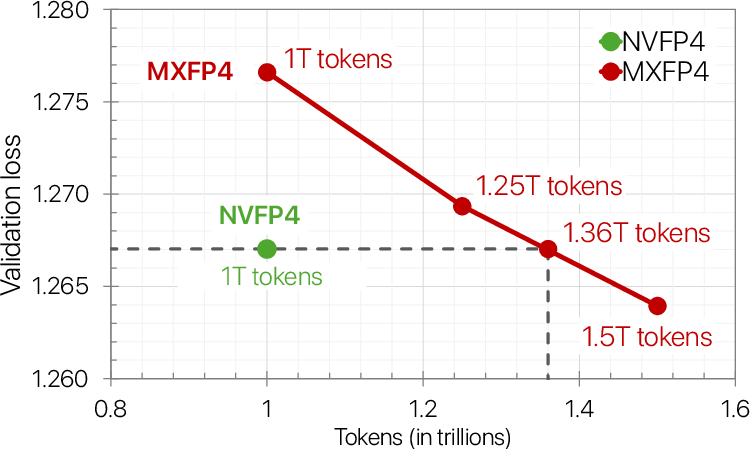
Figure 2: Relative difference between training loss of BF16 (baseline) and NVFP4 and MXFP4 pretraining, highlighting NVFP4's superior convergence.

Downstream task accuracies (MMLU, AGIEval, GSM8k, etc.) are nearly identical between NVFP4 and FP8, with the exception of minor discrepancies in coding tasks, likely attributable to evaluation noise. Notably, NVFP4 achieves an MMLU-pro accuracy of 62.58%, compared to 62.62% for FP8.

Precision Switching

Switching from NVFP4 to higher precision (BF16) during the final stages of training further closes the loss gap, with most of the improvement attributable to switching the forward pass tensors. This strategy allows the majority of training to be performed in FP4, with only a small fraction in higher precision, optimizing both efficiency and final model quality.

Figure 3: Switching to higher precision towards the end of training reduces the loss gap for a 12B model, demonstrating a practical recipe for loss recovery.

NVFP4 vs MXFP4

Comparative experiments with MXFP4 show that NVFP4 consistently achieves lower training loss and requires fewer tokens to reach comparable validation perplexity. MXFP4 matches NVFP4 only when trained on 36% more tokens, underscoring NVFP4's efficiency advantage.

Ablation and Sensitivity Analyses

Extensive ablation studies reveal:

• Layer Sensitivity: Final linear layers are most sensitive to FP4 quantization; retaining them in BF16 is critical for stability.
• Stochastic Rounding: Essential for gradients, but detrimental for activations and weights.
• Hadamard Matrix Size: $16 \times 16$ matrices provide a good trade-off between accuracy and computational cost; larger matrices offer diminishing returns.
• Randomization: A single fixed random sign vector suffices for RHT; further randomization yields no measurable benefit at scale.
• Consistency in Scaling: 2D block scaling for weights is necessary to maintain consistent quantization across passes and preserve the chain rule.

Practical and Theoretical Implications

The demonstrated methodology enables stable, efficient pretraining of large LLMs in 4-bit precision, with minimal loss in accuracy relative to FP8. This has direct implications for reducing compute, memory, and energy requirements in frontier model development. The techniques outlined—especially 2D scaling and RHT—are likely to generalize to other narrow-precision formats and architectures, including mixture-of-experts and attention-centric models.

Theoretically, the work highlights the importance of preserving numerical consistency and unbiased gradient estimation in extreme quantization regimes. The chain rule violation induced by inconsistent quantization is a critical failure mode, and the proposed 2D scaling offers a robust solution.

Future Directions

Key avenues for future research include:

• Quantizing all linear layers without loss of convergence, further reducing reliance on high-precision layers.
• Extending NVFP4 quantization to attention and communication paths.
• Evaluating NVFP4 on larger models, longer token horizons, and alternative architectures.
• Investigating scaling laws for FP4 formats and their impact on sample efficiency.
• Exploring post-training quantization and inference scenarios.

Conclusion

This report establishes NVFP4 as a viable format for large-scale LLM pretraining, supported by a rigorous methodology that ensures stability and accuracy. The empirical results demonstrate that NVFP4, when combined with targeted algorithmic techniques, matches FP8 performance while delivering substantial efficiency gains. The findings provide a foundation for future work in narrow-precision training and open the door to more resource-efficient frontier model development.