A Systematic Study of Model Merging Techniques in Large Language Models (2511.21437v1)

Abstract: Model merging combines multiple fine-tuned checkpoints into a single model without additional training, offering an attractive approach to reusing models and efficiently improving performance. However, it remains unclear whether the advantages reported for smaller models and classifiers generalize to LLMs. We present a large-scale, systematic evaluation of six state-of-the-art merging methods, including recent subspace methods, across four open-weight LLMs, twelve fine-tuned checkpoints per base model, and sixteen standard LLM benchmarks. Evaluating through standardized benchmarks, we measure both the probability that a merged model outperforms the base model and relative gains over the best individual checkpoint. Our results show that the oldest and simplest method, Task Arithmetic, is the only approach that reliably yields performance gains on LLMs. Other interference-aware and subspace merging methods typically result in significant performance drops. Our findings indicate that current merging techniques do not directly transfer to modern LLMs. This motivates the design of LLM-specific merging algorithms and merging-aware fine-tuning methods. Code will be released upon acceptance of this paper.

• The paper demonstrates that Task Arithmetic consistently yields constructive interference in LLMs, achieving success rates of 80–100% and a mean gain of +1.62 for Llama 8B with 10 merged checkpoints.
• The study systematically compares six merging techniques—including Task Arithmetic, TIES-Merging, and subspace-based methods—across four LLM architectures and 16 benchmark suites.
• The findings highlight the need for LLM-specific merging strategies that account for complex parameter geometries to prevent catastrophic forgetting and optimize multi-task integration.

Systematic Evaluation of Model Merging Methods for LLMs

Introduction and Motivation

This work presents an extensive, rigorously controlled analysis of model merging techniques applied to LLMs, focusing on the transferability of popular algorithms from small-scale settings and vision/LLMs to multi-billion-parameter LLMs. The motivation for model merging arises from the proliferation of fine-tuned checkpoints, which, if effectively merged, promise substantial gains in practitioner efficiency and resource allocation by obviating repeated fine-tuning and enabling composition of multiple capabilities into a single model. The paper investigates if constructive interference—where merged models outperform their constituent experts—is reliably achievable in standard LLM use cases.

Figure 1: Experimental protocol that matches base LLMs to sets of 12 fine-tuned checkpoints, applies merging algorithms, and evaluates all outputs on a broad suite of benchmarks to assess universal trends in LLM model merging.

Model Merging Algorithms: Task Arithmetic and Subspace Methods

The work systematically evaluates six representative merging methods grouped into task vector–based and subspace-based paradigms. These include Task Arithmetic (TA), TIES-Merging, Model Stock (all weight interpolation based), and TSV-Merge, Iso-C, Subspace Boosting (subspace-based approaches).

Task Arithmetic merges models by linearly combining parameter deltas (task vectors) with respect to a base. TIES-Merging introduces additional sparsification and sign-consensus filtering steps to reduce cross-task interference, while Model Stock interpolates between the base and geometric mean of fine-tuned checkpoints, with a layer-wise angular correction.

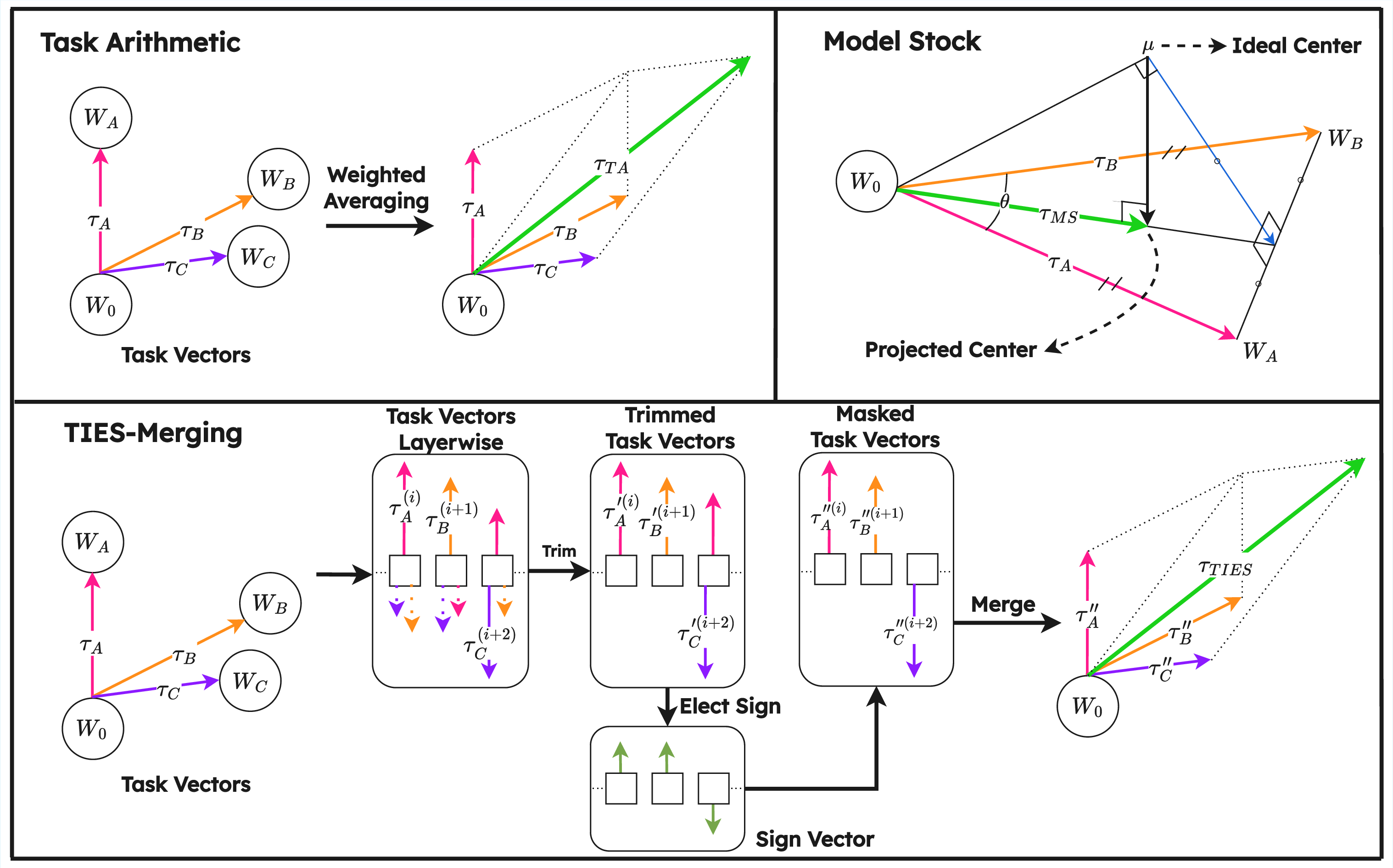
Figure 2: Schematic comparison of Task Arithmetic, TIES-Merging, and Model Stock mechanisms. Each method generalizes vector arithmetic in distinct ways to mitigate interference and optimize knowledge transfer in parameter space.

Three subspace-based methods attempt to align, compress, and isotropize update directions in low-rank subspaces via SVD decomposition and spectrum manipulation, aiming to reduce destructive interference that may arise when merging unrelated or orthogonal task domains.

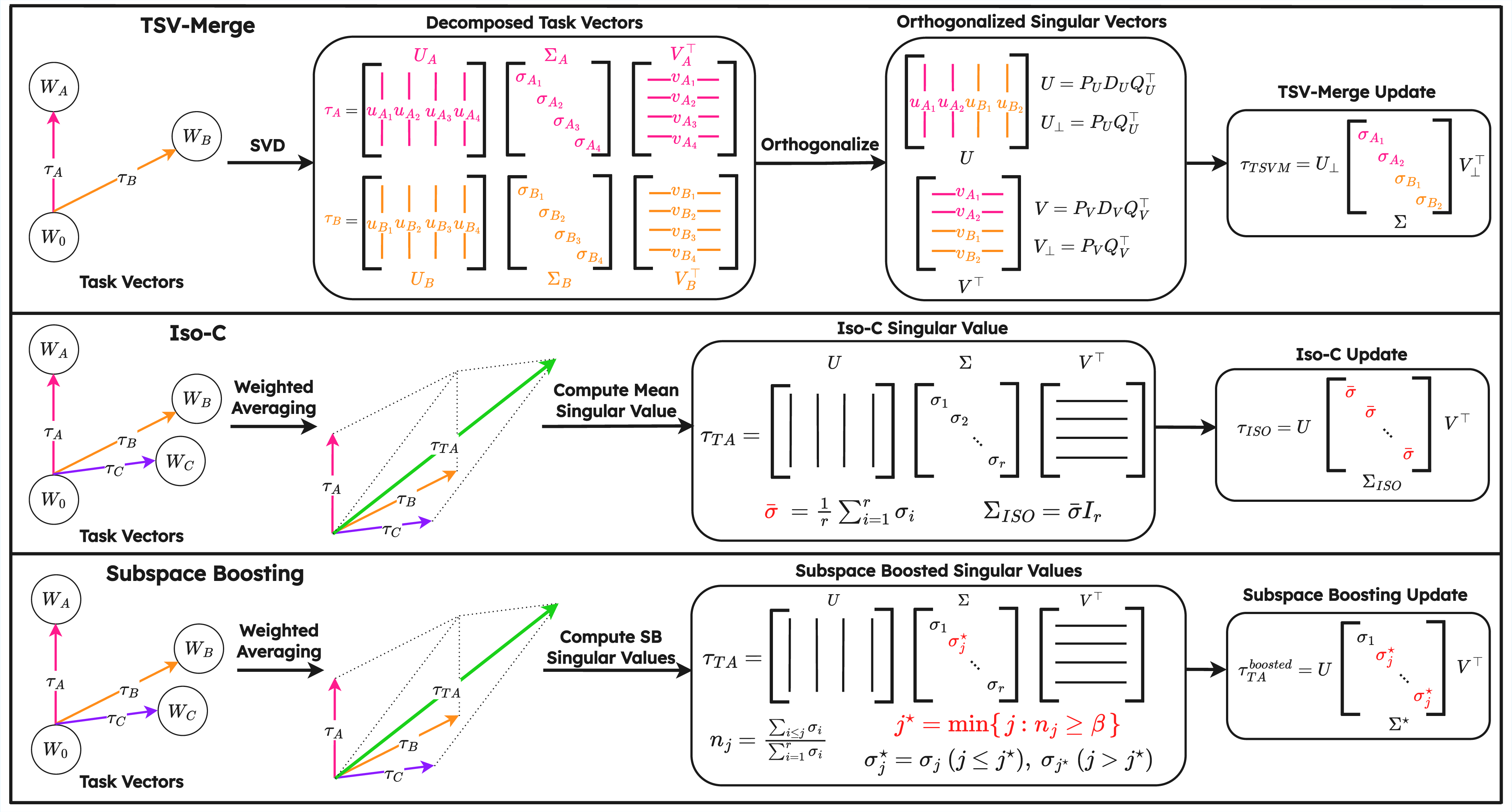
Figure 3: Illustration of subspace-based methods showing how they extract, align, and boost task-specific directions to mitigate rank collapse and broaden the mergeable subspace of model updates.

Experimental Protocol and Benchmarks

The primary experimental axes comprise four open-weight LLM architectures (Qwen3 4B/8B, Llama3 3.2B/8B), each paired with 12 fine-tuned variants sampled from heterogeneous domains. Each base model and merged output is assessed across 16 standardized benchmarks spanning commonsense reasoning, question answering, scientific and instruction-following challenges (ARC, HellaSwag, MMLU, MedMCQA, BoolQ, and others). For each merge order (from 2 up to 12), combinations of checkpoints are randomly sampled to provide representative coverage.

Quantitative Results and Constructive Interference Analysis

TA consistently produces monotonic improvements over the base models and individual experts as the number of merged checkpoints increases. Constructive interference is reliably observed once 4 or more checkpoints are merged, with success rates reaching 80–100% and mean relative improvements peaking at +1.62 for Llama 8B at $n=10$. Individual fine-tuned checkpoints rarely outperform their base models, confirming that gains are attributable to true interaction rather than mere selection of strong experts. Model Stock gives marginal, consistently positive results but with lower amplitude, while TIES-Merging generally degrades model performance due to excessive deviation from the base parameters.

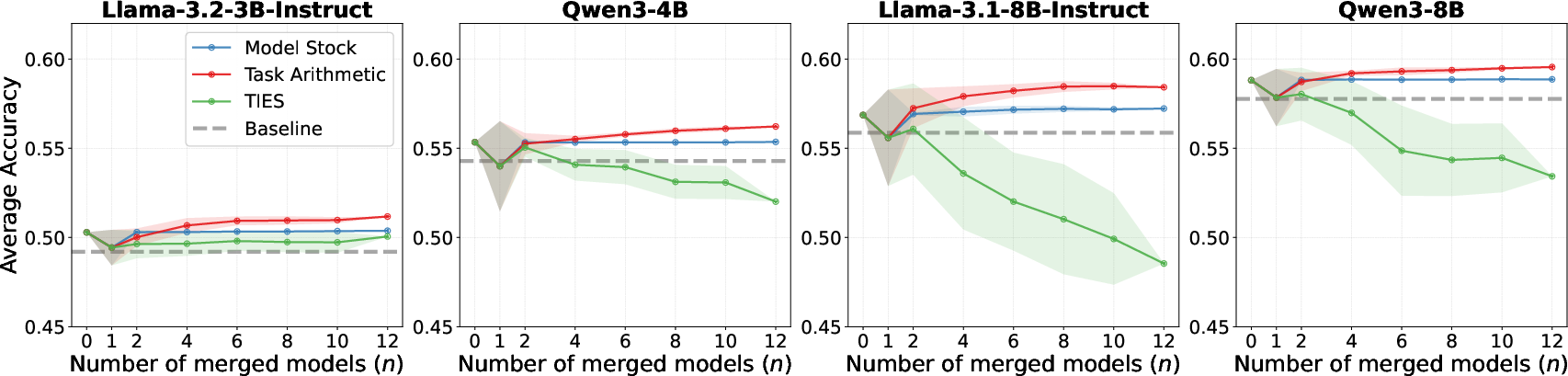
Figure 4: Accuracy comparison across benchmark suites for all base and merged models, quantifying improvement trends and stability for each merging method.

Parametric distance analyses show that successful methods (TA, Model Stock) induce only small $L_2$ displacements from the base and remain within the base model’s loss basin, while TIES-Merging and subspace-based methods shift too far and trigger catastrophic forgetting.

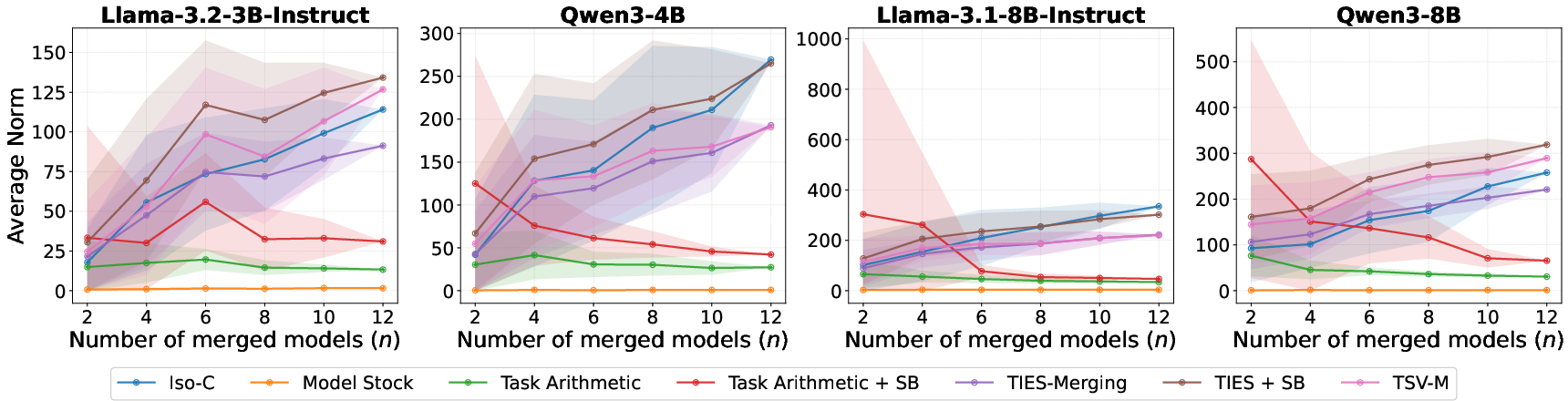
Figure 5: $L_2$ distance of merged weights to the base model, highlighting the correlation between excessive shift in parameter space and degraded model performance.

Subspace-based approaches—TSV-Merge, Iso-C, and Subspace Boosting—fail to generalize their previously reported benefits to LLMs. Their progressive truncation, orthogonalization, or spectrum flattening suppresses informative update directions when applied to diverse, randomly sampled fine-tuned variants. Only TA + Subspace Boosting can match or slightly surpass pure TA at large merge numbers, but this is attributed to the robustness of TA itself rather than genuine efficacy of subspace boosting.

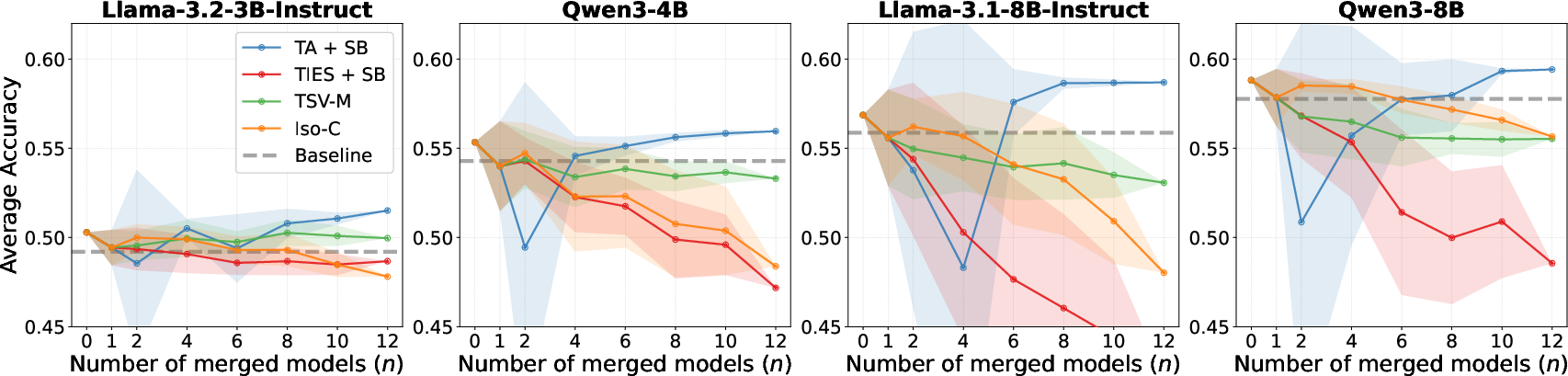
Figure 6: Comparative accuracy results for subspace-based methods and baseline algorithms showing negative scaling and failure of constructive interference as the number of merged checkpoints increases.

Taskwise and Hyperparameter Studies

Taskwise evaluation at the benchmark level confirms that TA (and TA + Subspace Boosting) maintain or increase performance across a broad array of axes (reasoning, knowledge, instruction-following), while alternative algorithms deteriorate as merge order rises. The effect of hyperparameters (e.g., TA mixing coefficient $\lambda$, TIES density $k$, Subspace Boosting threshold $\beta$) reveals sensitivity only in regimes far from optimal, with robust settings available that prevent further degradation.

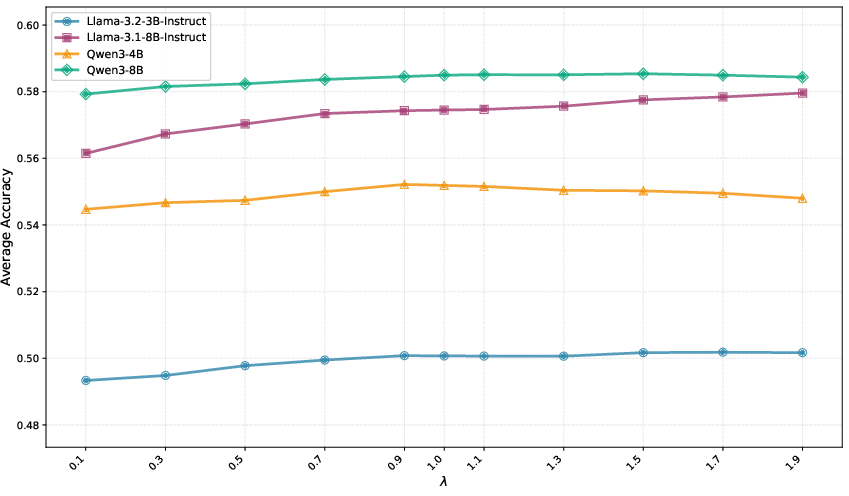
Figure 7: Effect of the TA mixing coefficient $\lambda$ with performance saturating for $\lambda \sim 1$.

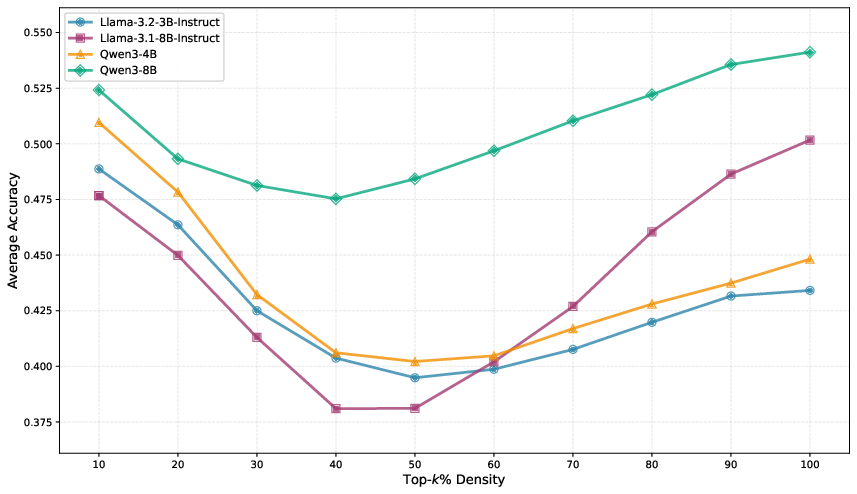
Figure 8: Impact of TIES-Merging density $k$ showing optimality at extreme values.

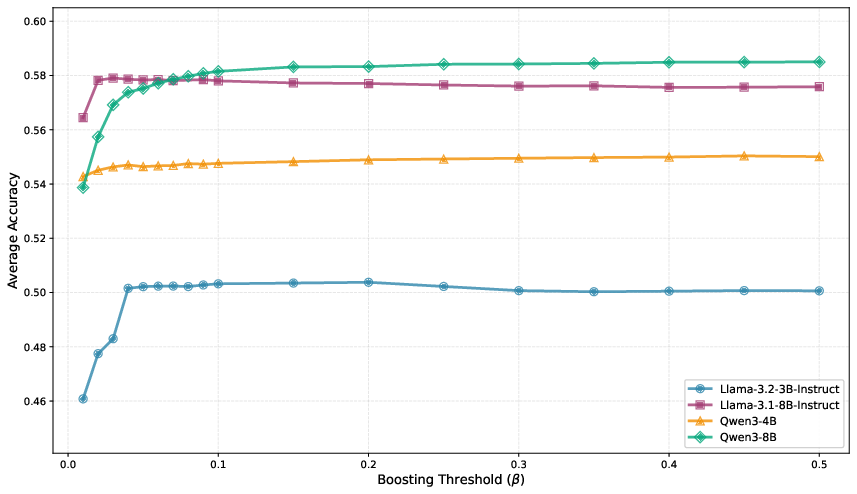
Figure 9: Subspace Boosting threshold $\beta$ sweeps showing rapid stabilization and non-critical dependence for moderate $\beta$.

Methodological and Practical Implications

The primary claim is that, for LLMs, only primitive averaging schemes (TA) reliably achieve constructive interference during model merging. Interference-aware and subspace-based algorithms—despite strong results in vision and encoder-decoder settings—do not translate to open-weight LLMs with heterogeneously fine-tuned checkpoints. The failure mode is attributed to lack of orthogonally separated update directions, excessive pruning/isotropization, and nontrivial geometry of the LLM parameter landscape. The paper rigorously demonstrates that existing methods are not sufficiently robust for arbitrary checkpoint merging in deployment and motivates LLM-specific algorithm development and merging-aware fine-tuning strategies.

Future Directions

The findings suggest that the future of LLM model merging lies in developing methods explicitly designed for LLM architectures and fine-tuning landscapes. This necessitates understanding parameter space geometry, disentangling capabilities through specialized fine-tuning, and designing algorithms that exploit mode connectivity rather than brute-force subspace operations. Practical impacts may include resource-efficient deployment, better multi-task integration, and more principled approaches to catastrophic forgetting prevention.

Conclusion

In summary, only the simplest merging heuristics (Task Arithmetic) yield robust performance improvements for model merging in LLMs, where alternatives often degrade accuracy, contradicting earlier results in smaller-scale or vision encoder-decoder domains. Theoretical and practical progress in LLM merging demands new approaches tailored to the architectural and fine-tuning idiosyncrasies of LLMs, as well as merging-aware engineering practices for checkpoint design and deployment.

Reference: "A Systematic Study of Model Merging Techniques in LLMs" (2511.21437).