HERMES: Towards Efficient and Verifiable Mathematical Reasoning in LLMs (2511.18760v1)
Abstract: Informal mathematics has been central to modern LLM reasoning, offering flexibility and enabling efficient construction of arguments. However, purely informal reasoning is prone to logical gaps and subtle errors that are difficult to detect and correct. In contrast, formal theorem proving provides rigorous, verifiable mathematical reasoning, where each inference step is checked by a trusted compiler in systems such as Lean, but lacks the exploratory freedom of informal problem solving. This mismatch leaves current LLM-based math agents without a principled way to combine the strengths of both paradigms. In this work, we introduce Hermes, the first tool-assisted agent that explicitly interleaves informal reasoning with formally verified proof steps in Lean. The framework performs intermediate formal checking to prevent reasoning drift and employs a memory module that maintains proof continuity across long, multi-step reasoning chains, enabling both exploration and verification within a single workflow. We evaluate Hermes on four challenging mathematical reasoning benchmarks using LLMs of varying parameter scales, from small models to state-of-the-art systems. Across all settings, Hermes reliably improves the reasoning accuracy of base models while substantially reducing token usage and computational cost compared to reward-based approaches. On difficult datasets such as AIME'25, Hermes achieves up to a 67% accuracy improvement while using 80% fewer total inference FLOPs. The implementation and codebase are publicly available at https://github.com/aziksh-ospanov/HERMES.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces Hermes, a smart math-solving system that works with LLMs like AI “students.” Hermes helps them think through math problems step by step while making sure each step is actually correct. It does this by mixing two styles of math:
- Informal reasoning: normal text explanations in plain language (like how people write solutions).
- Formal reasoning: exact, checkable steps in a special math language called Lean4 that a computer can verify.
The goal is to get the best of both worlds: flexible thinking plus rock-solid correctness.
What questions does the paper ask?
The paper focuses on three simple questions:
- How can we stop AI models from making tiny mistakes that grow into wrong answers during long math reasoning?
- Can we check important steps while the AI is working, instead of only checking at the end?
- Will this make the AI both more accurate and more efficient (using fewer tokens and less compute)?
How does Hermes work?
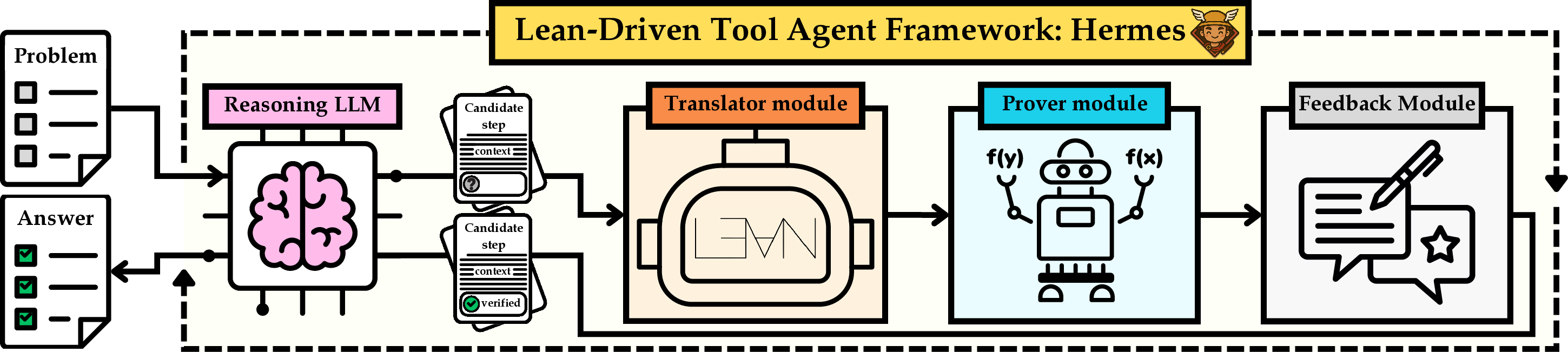
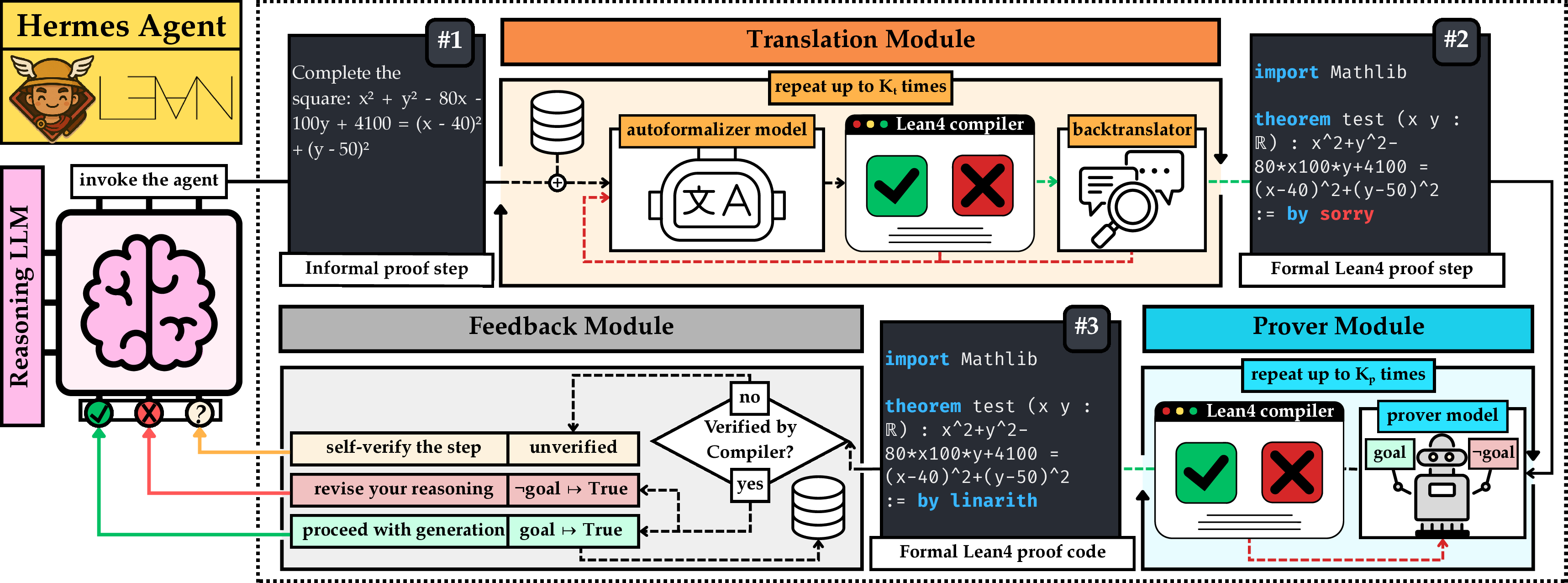
Think of Hermes as a team of helpers around the AI:
- The “AI student” writes its next reasoning step in normal text.
- A “translator” turns that step into Lean4 code (Lean4 is like a strict math checker that never lets mistakes slide).
- A “prover” tries to prove the step in Lean4—or prove its opposite to catch errors.
- A “memory” keeps track of correct earlier steps so the AI doesn’t forget or contradict itself.
- A “feedback loop” sends the result back to the AI: “That step is correct” or “Nope—try again.”
Here’s a short list of the main modules:
- LLM reasoning: the AI thinks in plain language.
- Translation: turns a sentence into Lean4 math code.
- Prover: tries to prove the step or show it’s wrong.
- Memory: stores verified steps and retrieves the most relevant ones to stay consistent.
- Feedback: tells the AI what worked so it can adjust its next move.
Everyday analogy: It’s like writing a proof with a very strict math teacher standing next to you. After every important sentence, the teacher checks it instantly. If it’s wrong, you fix it before moving on. Plus, the teacher keeps notes on what you’ve already proven so your new steps don’t contradict your earlier claims.
Two simple settings adjust how hard Hermes tries:
- : how many times the translator tries to produce good Lean4 code.
- : how many proof attempts the prover makes.
Higher values can improve accuracy but cost more time/compute.
What did they find?
The authors tested Hermes on four tough math benchmarks and with different AI models (small, medium, and large). Here are the key outcomes:
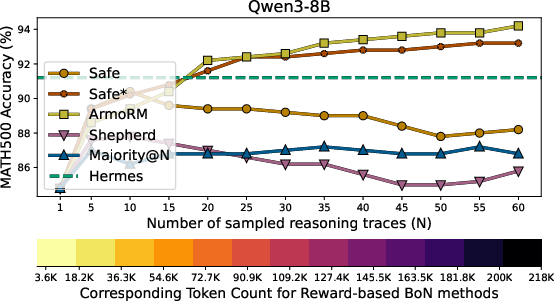
- Accuracy improved across all tests. On the difficult AIME’25 dataset, Hermes boosted accuracy by up to 67% compared to the base AI model.
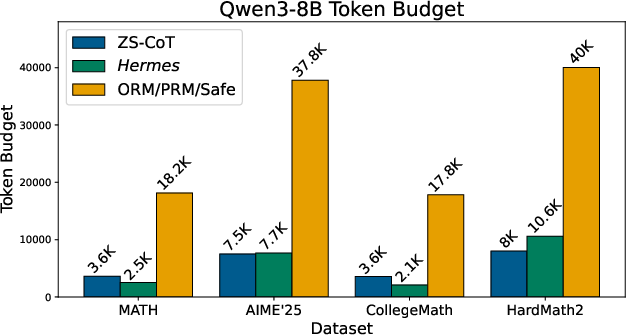
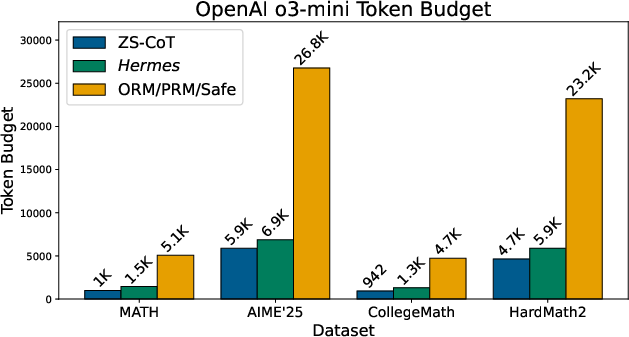
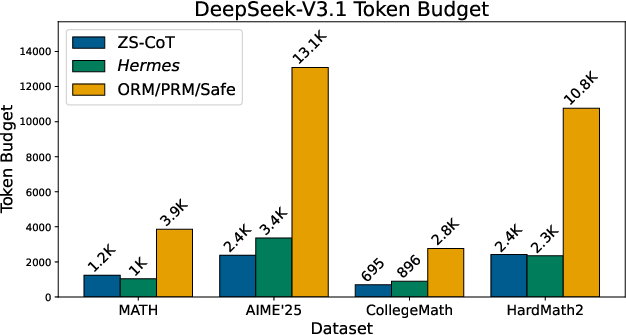
- Hermes used far fewer tokens than reward-based methods (systems that score either the final answer or each step to pick the best solution). In many cases, Hermes used about 4–6 times fewer tokens than those scoring approaches.
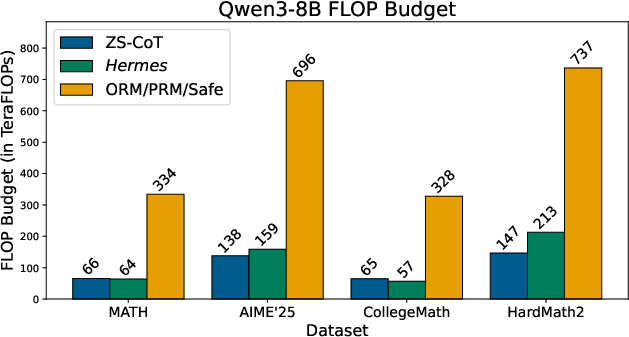
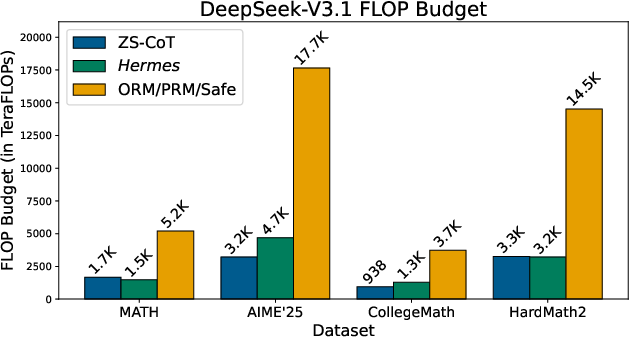
- Compute was also lower: even though Hermes checks steps with Lean4, its total cost stayed similar to standard chain-of-thought and much lower than reward-based methods. The paper reports up to 80% fewer inference FLOPs in some settings.
- Important parts of Hermes matter: removing the prover or memory module made accuracy drop—especially on harder problems that need longer, more careful reasoning.
- Tuning (translations) and (proof attempts) helps. Moderate values (like 4) gave a good balance of accuracy and speed.
Why this is important:
- It prevents “reasoning drift,” where small errors build up in long solutions.
- It gives clear, interpretable feedback: not just a score, but a proof or a counterproof.
- It makes problem solving more reliable without ballooning token usage.
Why does this matter?
Hermes shows a practical way to make AI math reasoning both smarter and safer:
- For students and teachers: it encourages step-by-step thinking and catches mistakes early.
- For researchers: it’s a clean bridge between flexible natural-language reasoning and precise formal math checking.
- For future AI systems: it suggests that mixing tools (like Lean4) with LLMs can improve reliability, reduce hallucinations, and cut costs.
In short, Hermes helps AI “think like a human” but “check like a computer,” making tough math more accurate, efficient, and trustworthy.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, focused list of what remains missing, uncertain, or unexplored in the paper, phrased to be concrete and actionable for future work.
- Step selection policy: The paper does not specify how “critical” proof steps are chosen for verification. Evaluate strategies (verify-all vs. heuristic selection vs. PRM-guided selection) and quantify their impact on accuracy, cost, and latency.
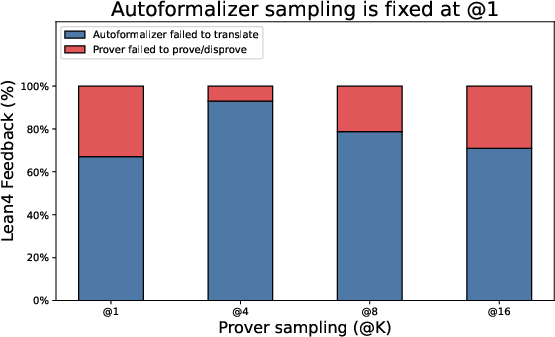
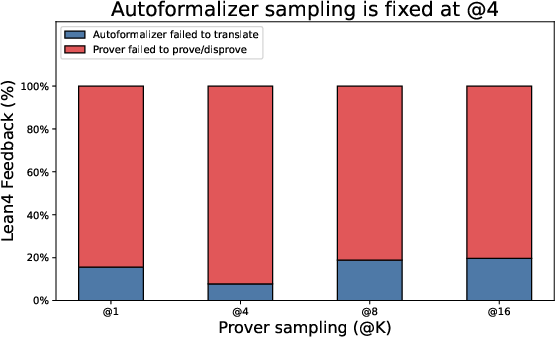
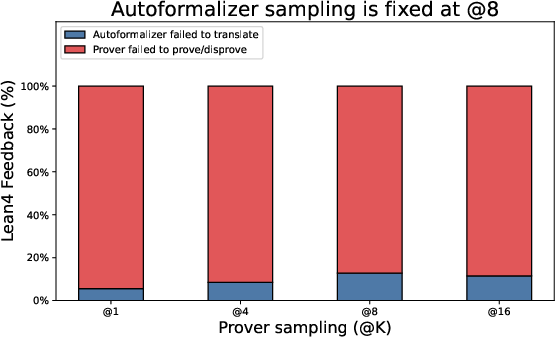
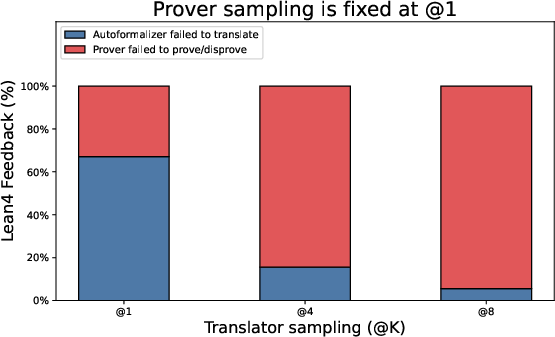
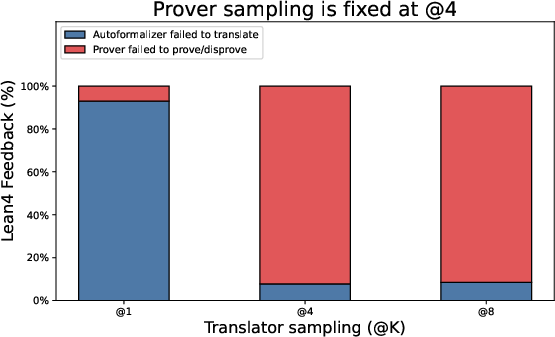
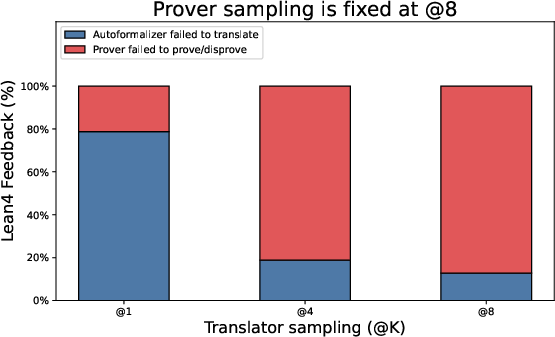
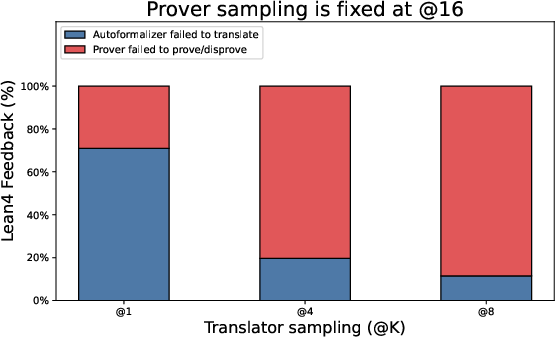
- Autoformalization reliability: Backtranslation equivalence is judged by an LLM, not a formal semantic checker. Measure false-positive/negative rates of the translation–backtranslation loop and develop more reliable equivalence tests (e.g., canonicalization, symbolic normalization, proof obligations).
- Translation and backtranslation ablations: No ablation isolating the translator’s contribution (success rate, error types, sensitivity to domain/notation). Report per-step translation success rates and failure taxonomy across benchmarks.
- Handling ambiguous or underspecified natural language: Many math problems contain implicit assumptions. Study how Hermes detects and resolves ambiguities during autoformalization (e.g., type disambiguation, domain constraints, quantifier scope).
- Verification signal granularity: REPL feedback is a coarse True/False/Failure signal. Investigate richer signals (proof length, tactics used, lemma provenance, confidence/timeout reason) and quantify whether they improve downstream reasoning and planning.
- Failure-mode disambiguation: “Verification failed” conflates timeout, undecidability, poor translations, and prover search failure. Add failure-class labeling and adaptive recovery strategies for each class; measure gains.
- Negation proving policy: Proving both the goal and its negation can be costly or misleading in constructive settings. Clarify logic assumptions (classical vs. constructive), define when negation is attempted, and evaluate the utility/cost of counterexample discovery.
- Memory correctness and poisoning: Memory stores “validated” steps, but translation errors can validate wrong claims. Quantify memory poisoning rates, add contradiction checks (e.g., SAT/SMT consistency), and implement rollback/conflict resolution.
- Memory retrieval design: Only Qwen3-Embedding with top‑k=3 is evaluated. Compare embedding models, k-values, re-ranking methods, and context formatting; add adaptive retrieval (e.g., query-dependent k) and measure effects.
- Incorporating memory as hypotheses: The pipeline injects retrieved claims into Lean as hypotheses. Audit whether this ever biases proofs toward incorrect goals or introduces hidden assumptions; develop safeguards (e.g., hypothesis provenance tags, mandatory re-verification).
- Adaptive budgets: K_t and K_p are fixed globally. Explore adaptive budget allocation per step/problem using bandit/early-stopping criteria or verifier-calibrated confidence, and quantify trade-offs in cost and accuracy.
- Timeouts and scheduler: Lean timeout is fixed at 60s, and a verification scheduler is mentioned without details. Characterize how scheduling policies, parallelization, and timeout tuning affect throughput and success rates under realistic resource constraints.
- Compute accounting fidelity: FLOPs estimates ignore autoformalizer/prover model FLOPs, KV cache reuse, token-by-token generation, and tool-call overhead. Provide end-to-end wall-clock, GPU memory, and energy measurements and a more faithful compute model.
- Token cost comparability: Token budget comparisons exclude tool-side costs when tools are accessed via APIs. Standardize cost reporting to include tool calls (tokens or local FLOPs) for fair comparisons.
- Benchmark coverage: Benchmarks are math word/problem sets; formal theorem-proving datasets (e.g., MiniF2F, PutnamBench, IMO-formal) are not systematically evaluated. Test Hermes on formal benchmarks and domain-specific areas (geometry, number theory) to assess generality.
- Statistical rigor: No confidence intervals or statistical significance reported. Add bootstrapped CIs, per-category breakdowns, and robust significance testing across datasets and models.
- Interpretability validation: Hermes claims step-level interpretability, but no user studies or formal metrics are provided. Design human-in-the-loop evaluations and quantitative measures of interpretability/usefulness.
- Error analysis: The paper lacks a qualitative taxonomy of typical errors (translation, proof search, memory misuse, planning errors). Provide representative failure cases and targeted mitigations.
- Closed-model reproducibility: Results rely on OpenAI o3-mini; architecture and weights are not public. Offer replication using open models and publish prompts, seeds, agent policies, and tool versions to ensure reproducibility.
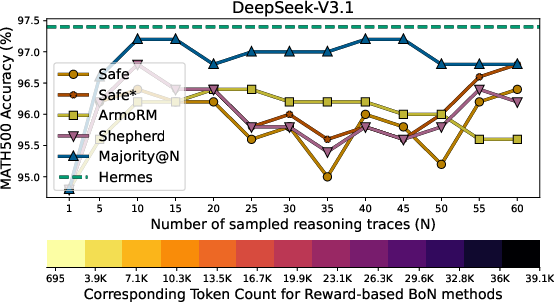
- Multi-sample Hermes: Hermes is evaluated at @1; the effect of sampling multiple Hermes trajectories (e.g., @n with diversity) is unexplored. Assess accuracy–cost trade-offs and compare against BoN baselines fairly.
- Synergy with PRMs/ORMs: Reward models are only used as baselines. Investigate hybrid designs where PRMs/ORMs guide which steps to verify or provide priors for search, and measure combined gains.
- Training-time integration: Hermes is purely inference-time. Explore fine-tuning reasoning models using verifier feedback (e.g., supervised traces, reinforcement learning with formal rewards) and assess sample efficiency.
- Domain transfer beyond Lean4: Portability to Coq/Isabelle and cross-system consistency is not explored. Evaluate Hermes with multiple proof assistants, quantify translation portability, and identify library/axiom gaps.
- Library coverage and dependency management: Success may depend on Mathlib coverage and tactic availability. Analyze dependency bottlenecks, add automated lemma discovery/premise selection, and report where library gaps cause failures.
- Robustness to adversarial inputs: No tests on adversarially perturbed or noisy problems. Benchmark robustness and introduce defenses (e.g., input sanitization, ambiguity flags, multi-view formalization).
- Decidability and expressivity limits: Some statements may be out-of-scope for Lean or require classical axioms. Catalog these cases, define fallbacks (numeric solvers, CAS, SMT), and evaluate integration.
- Counterexample surfacing: When negation proofs exist, Hermes reports “counter-proof found” but does not surface explicit counterexamples to the user. Add counterexample extraction and assess its impact on reasoning corrections.
- Long-horizon stability: Claims about preventing error propagation are plausible but not quantified. Track step-wise correctness over long chains, measure drift, and evaluate whether memory+verification reduces cascading errors.
- Policy specification: The LLM’s decision rules after feedback (“continue, revise, or alternative approach”) are unspecified. Formalize and compare decision policies (e.g., thresholded confidence, planner modules) and quantify their effects.
- Coverage of numerical vs. symbolic tasks: How Hermes handles numeric approximations, inequalities, and answer formats (AIME-style integers) is not analyzed. Audit mismatches between informal numeric answers and formal symbolic goals.
- Real-time applicability: Latency and interactive use are not discussed. Measure end-to-end latency and explore incremental verification for real-time tutoring or interactive proof environments.
Glossary
- Autoformalization: The automated translation of informal mathematical text into a formal language suitable for proof assistants. "Recent work in autoformalization, translating informal mathematical statements into formal statements, has made rapid advancements."
- Autoformalizer: A model that converts natural-language mathematical statements into formal statements (e.g., Lean). "a dedicated Lean autoformalizer model"
- Back-translation: Translating a formalized statement back into natural language to check semantic fidelity with the original. "verifies translation consistency through back-translation"
- Best-of-N (BoN): An evaluation strategy that selects the best output from N generated candidates. "report Best-of-N (BoN)."
- Chain-of-Abstraction: A tool-usage strategy that abstracts and structures multi-step reasoning for more effective tool application. "introduced Chain-of-Abstraction to better leverage tools in multi-step reasoning"
- Chain-of-Thought (CoT): A prompting approach that elicits step-by-step reasoning in LLMs. "the Chain-of-Thought (CoT) approach"
- Counter-proof: A formal proof of the negation of a proposed statement, demonstrating its invalidity. "derive a counter-proof (e.g., a counterexample)"
- Deterministic verifier-guided reasoning: A reasoning process steered by a verifier with deterministic guidance rather than stochastic scoring. "explores deterministic verifier-guided reasoning."
- Embedding-based retrieval: Retrieving relevant context using vector representations and similarity search. "embedding-based retrieval and ranking"
- FLOPs: A measure of computational cost in terms of floating-point operations. "total inference FLOPs."
- Formal theorem proving: Constructing machine-checkable proofs in a proof assistant under a formal logical system. "formal theorem proving provides rigorous, verifiable mathematical reasoning"
- Gaokao-Formal: A benchmark dataset of formally represented mathematics used to evaluate autoformalization and proving. "the Gaokao-Formal benchmark."
- Lean goal: A target statement in Lean that the prover attempts to establish as true. "translates the natural-language statement into Lean goal"
- Lean tactics: Built-in scripted proof procedures in Lean that automate common proof steps. "built-in tactics in Lean"
- Lean4: A modern interactive theorem prover and programming language used for formal verification. "Lean4-driven, multi-modular reasoning agent"
- Lean4 compiler: The Lean component that checks the correctness and type consistency of formal code and proofs. "did not pass the Lean4 compiler."
- Lean4 REPL: The read–eval–print loop interface for interacting with Lean4 programmatically. "the Lean4 REPL"
- LeanScorer: A scoring mechanism introduced for assessing autoformalization outputs in Lean. "a novel "LeanScorer" for assessment"
- Memory block: A module that stores and retrieves validated proof steps to maintain cross-step coherence. "Memory Block is responsible for collecting all validated proof steps"
- Neuro-symbolic: Approaches that combine neural methods (e.g., LLMs) with symbolic logic or formal verification. "neuro-symbolic reasoning"
- Outcome Reward Model (ORM): A model that assigns a score to the final solution quality of a reasoning process. "Outcome Reward Models (ORMs)"
- Premise-selection theorem prover: A prover that prioritizes or selects relevant premises to guide formal proof search. "premise-selection theorem provers"
- Process Reward Model (PRM): A model that scores intermediate reasoning steps to guide the reasoning trajectory. "Process Reward Models (PRMs)"
- Proof assistant: Software that aids in constructing and verifying formal proofs within a logical framework. "proof assistants with trusted kernels"
- Reasoning drift: The gradual deviation of a reasoning process from correct or consistent logic over multiple steps. "prevent reasoning drift"
- Sledgehammer: An automated tool in Isabelle/HOL that integrates external provers into interactive proof development. "Sledgehammer in Isabelle"
- sorry placeholder: A Lean placeholder indicating an unfinished proof part that allows code to compile temporarily. "inserting a \lstinline{sorry} placeholder."
- Top-k retrieval: Selecting the k most relevant items (e.g., prior steps) based on similarity for contextual reasoning. "top- retrieval mechanism"
- Tool-calling capability: The ability of an LLM to invoke external tools during generation to verify or augment its reasoning. "tool-calling capability of modern LLMs"
- Trusted kernel: The small, verified core of a proof assistant responsible for checking proof correctness. "trusted kernels such as Lean4"
- Verification scheduler: A component that parallelizes formal verification tasks to speed up inference. "the verification scheduler, which parallelizes Lean code verification"
- Whole-proof generation model: A model that attempts to produce complete formal proofs rather than isolated steps. "we incorporate a whole-proof generation model"
- Zero-shot chain-of-thought: Generating step-by-step reasoning without task-specific examples or fine-tuning. "a zero-shot chain-of-thought baseline"
Practical Applications
Immediate Applications
The following applications can be deployed now by integrating Hermes’s Lean4-driven, tool-augmented reasoning (translation, prover, memory, feedback) into existing systems and workflows.
- Verified math tutoring and homework assistance
- Sector: Education
- What: Step-by-step math tutoring where each critical step is autoformalized and verified in Lean4 to prevent reasoning drift and hallucinations; interactive guidance when steps fail verification.
- Tools/products/workflows: LMS plugin or “Hermes Tutor” copilot; grading assistant that checks student solutions by translating steps to Lean4 goals; AIME/college math practice apps with per-step verification and counterexample feedback.
- Assumptions/dependencies: Coverage of math library (Mathlib) for target curricula; reliable autoformalization for typical problem formats; tool-calling LLM access; modest compute for Lean REPL.
- Auto-graded proofs and assignments
- Sector: Education/Academia
- What: Automated scoring of student solutions based on formally verified intermediate steps and consistency across steps via Hermes’s memory block.
- Tools/products/workflows: Instructor console for batch verification; “proof continuity” rubric using Hermes memory; back-translation-based equivalence checks for natural-language proofs.
- Assumptions/dependencies: Students’ statements must be mappable to Lean4; institutional acceptance of formal verification as grading criterion.
- Math research assistance for lemma discovery and proof repair
- Sector: Academia/Research
- What: Draft, verify, and iteratively repair proof sketches; counter-proof (negation) attempts surface contradictions or missing assumptions.
- Tools/products/workflows: “Lean scratchpad” for exploratory proving; authoring assistants that interleave informal sketches with Lean tactics; verified lemma databases seeded by Hermes’s memory module.
- Assumptions/dependencies: Domain coverage in Lean4; reliable autoformalization for advanced topics; willingness to adopt neuro-symbolic tooling.
- Auditable quantitative analysis in scientific computation
- Sector: Academia/Software
- What: Verification of derivations in statistics, optimization, and numerical algorithms to reduce subtle errors in papers, reports, and code comments.
- Tools/products/workflows: CI hooks that formalize and verify key derivations; notebooks extensions that run Hermes checks on formula transformations; counterexample reports when derivations fail.
- Assumptions/dependencies: Availability of formal counterparts for target math; manageable translation overhead; compatible team workflows.
- “Reasoning firewall” for math-heavy LLM features
- Sector: Software (Developer tools, AI platforms)
- What: Gate LLM-generated quantitative answers through Hermes; only pass steps that compile and prove, otherwise request revisions.
- Tools/products/workflows: SDK to wrap math functions; production guardrails for on-call analytics, BI bots, or customer-facing calculators.
- Assumptions/dependencies: Tight integration with Lean4 REPL; latency budgets acceptable; coverage for the math used by product features.
- Spreadsheet and reporting verification
- Sector: Finance/Enterprise IT
- What: Formalize critical spreadsheet formulas and risk calculations; verify step-level correctness and flag logically inconsistent chains.
- Tools/products/workflows: “Hermes Audit” for spreadsheets; roll-up verification for aggregated metrics; counter-proof attempts to find inconsistencies.
- Assumptions/dependencies: Mapping spreadsheet expressions to Lean4 goals; domain libraries for finance math; change management for audit trails.
- Verified clinical and laboratory calculators
- Sector: Healthcare
- What: Use Hermes to verify dosing rules, risk scores, and unit conversions; flag unsafe or inconsistent calculations in decision support tools.
- Tools/products/workflows: Clinical calculator backend that formalizes rules; CI verification for medical software; on-call “math sanity check” for new rule sets.
- Assumptions/dependencies: Stable, formalizable formulae; regulatory acceptance of Lean4-based verification; rigorous validation of translator on clinical edge cases.
- Control/robotics stability proof checks (local properties)
- Sector: Robotics/Industrial automation
- What: Verify local stability conditions, inequality constraints, or safety margins for known controllers and planners.
- Tools/products/workflows: Hermes-enabled controller design notebooks; pre-flight checks that formalize key steps (Lyapunov inequalities, bounds).
- Assumptions/dependencies: Availability of Lean4 formalizations for control theory primitives; tractable goals (local proofs rather than full system verification).
- Operations research and optimization sanity checks
- Sector: Energy/Logistics
- What: Verify KKT conditions, dual bounds, or feasibility steps in optimization pipelines; detect reasoning drift in multi-step derivations.
- Tools/products/workflows: Hermes guardrails around OR solvers; report generators with verified derivation snippets and counterexamples when constraints are violated.
- Assumptions/dependencies: Formalization coverage for optimization constructs; integration with existing OR toolchains; acceptable latency.
- Dataset generation for training reward models and provers
- Sector: AI/Software
- What: Produce high-quality, verifiably labeled step-wise reasoning traces for PRMs/ORMs or supervised fine-tuning.
- Tools/products/workflows: Hermes pipeline to synthesize curated, verified datasets; label provenance via Lean compilation and memory context.
- Assumptions/dependencies: Compute budget for large-scale synthesis; diversity of tasks; careful selection of translator/prover budgets (Kt, Kp).
Long-Term Applications
These applications require further research, scaling of autoformalization/prover coverage, domain library growth, or tighter integration into safety-critical pipelines.
- End-to-end formalized STEM copilot (math/physics/econ)
- Sector: Education/Research/Software
- What: A general STEM assistant that interleaves informal derivations with machine-checked formal proofs across disciplines.
- Tools/products/workflows: Cross-domain Lean4 libraries; modular autoformalizers specialized per field; persistent proof memory across multi-session workflows.
- Assumptions/dependencies: Significant expansion of formal libraries beyond pure math; robust translation for domain-specific notation; improved backtranslation fidelity.
- Safety-critical verification for autonomous systems
- Sector: Robotics/Transportation
- What: Formal verification of planning and control logic, stability, and safety constraints at deployment scale; automated counterexample discovery.
- Tools/products/workflows: Hermes integrated into controller synthesis pipelines; “prove-or-revise” loops for mission planning; certification-ready audit trails.
- Assumptions/dependencies: Industrial-grade formal libraries; performance guarantees and deterministic behavior; regulatory alignment and tool qualification.
- Verified quantitative compliance reporting (finance and public policy)
- Sector: Finance/RegTech/Government
- What: Machine-checked derivations for regulatory submissions (risk, capital adequacy, climate metrics); formal audit trails of calculations.
- Tools/products/workflows: Policy-aligned verification schemas; standardized translators for disclosure templates; long-horizon memory for report continuity.
- Assumptions/dependencies: Standards bodies accept formal methods; secure, explainable integration; strong domain libraries for financial mathematics and econometrics.
- Formal correctness gate for enterprise AI assistants
- Sector: Software/Enterprise IT
- What: Enterprise assistants that refuse to produce math-heavy outputs unless Hermes verification succeeds; fallback flows that seek alternative derivations or data.
- Tools/products/workflows: Orchestrators that route LLM responses through Hermes; cross-tool “reasoning firewall” with error handling and human-in-the-loop escalations.
- Assumptions/dependencies: Coverage for diverse enterprise math; acceptable latency and cost at scale; governance policies that prefer formal correctness over speed.
- Scientific publishing with verifiable derivations
- Sector: Academia/Publishing
- What: Journals require machine-checkable derivations for key claims; reviewers use Hermes-based toolkits to assess consistency and identify gaps.
- Tools/products/workflows: Authoring templates that pair natural-language proofs with Lean4 goals; automated reviewer checks; public proof artifacts and memory-backed provenance.
- Assumptions/dependencies: Community adoption; accessible tooling for non-experts; broader formalization of statistics, modeling, and numerical methods.
- Formal verification in compilers and model serving (numerics)
- Sector: Software/ML Systems
- What: Prove invariants and numerical stability for compiled kernels, differentiable programming routines, or surrogate models’ analytic steps.
- Tools/products/workflows: Hermes hooks in build systems; automatic generation and proving of invariants; CI gates that enforce formal checks on critical paths.
- Assumptions/dependencies: Tight integration with compiler toolchains; tractable formalization of numerical kernels; scalable prover performance.
- Grid optimization and market mechanism verification
- Sector: Energy
- What: Proof-backed validation of market clearing rules, auction properties, and grid optimization steps (feasibility, optimality, fairness).
- Tools/products/workflows: Hermes-driven audits for operator pipelines; formal models of market mechanisms; counterexample testing on edge cases.
- Assumptions/dependencies: Extensive domain libraries for power systems and mechanism design; institutional buy-in; performance optimization for large instances.
- Verified clinical guideline translation to executable rules
- Sector: Healthcare
- What: Translate narrative guidelines into formal rules with machine-checkable steps; maintain continuity across updates using Hermes memory.
- Tools/products/workflows: Co-authoring tools for guideline committees; verified decision-support modules; traceable revisions with counter-proof flags.
- Assumptions/dependencies: High-quality, domain-specific autoformalization; harmonization with medical standards and EHR systems; regulatory processes.
- Robust training pipelines for reasoning LLMs using verified traces
- Sector: AI/Research
- What: Train next-generation reasoning models on Hermes-verified datasets to reduce hallucinations and improve step-wise correctness.
- Tools/products/workflows: Large-scale data synthesis with formal labels; curriculum learning from easy-to-hard goals; multi-model orchestration (translator/prover/selector).
- Assumptions/dependencies: Compute and data budgets; continued improvements in autoformalizer/prover accuracy; open, standardized repositories.
- Standards and certification for verifiable AI reasoning
- Sector: Policy/Governance
- What: Establish frameworks where AI outputs involving mathematics must pass machine-checkable verification; define acceptable failure modes and escalation paths.
- Tools/products/workflows: Conformance tests using Hermes; sector-specific verification schemas; certification programs and audits.
- Assumptions/dependencies: Multi-stakeholder consensus; interoperability across formal systems; legal and regulatory adoption.
Cross-cutting assumptions and dependencies
- Formalization coverage: Feasibility depends on the breadth and depth of Lean4 libraries (e.g., Mathlib) relevant to each domain.
- Translator reliability: Autoformalization and backtranslation must preserve semantics; higher sampling budgets (Kt) improve accuracy but increase runtime.
- Prover strength and budgets: Prover sampling (Kp) drives verification success; parallelized proof attempts (goal and negation) add robustness but require compute.
- Latency and cost: Hermes reduces token usage and FLOPs versus reward-based methods, but Lean verification adds overhead; acceptable tradeoffs vary by application.
- Tooling integration: Requires LLM tool-calling, Lean4 REPL access, and orchestration across modules (translation, prover, memory, feedback).
- Governance and acceptance: Institutional and regulatory bodies must accept formal verification as an audit mechanism, especially in healthcare, finance, and public policy.
- Human-in-the-loop: For ambiguous or out-of-coverage cases, workflows should include human review and iterative specification updates.
Collections
Sign up for free to add this paper to one or more collections.