Thinking Machines: Mathematical Reasoning in the Age of LLMs (2508.00459v1)

Abstract: LLMs have shown remarkable abilities in structured reasoning and symbolic tasks, with coding emerging as a particular area of strength. This success has sparked growing interest in applying LLMs to mathematics, both in informal problem-solving and formal theorem proving. However, progress in formal mathematics has proven to be significantly more difficult, despite surface-level similarities between programming and proof construction. This discrepancy raises important questions about how LLMs ``reason'', how they are supervised, and whether they internally track a notion of computational or deductive state. In this article, we address the state-of-the-art of the discipline, focusing on recent models and benchmarks, and explore three central issues at the intersection of machine learning and mathematical cognition: (i) the trade-offs between formal and informal mathematics as training domains; (ii) the deeper reasons why proof generation remains more brittle than code synthesis; (iii) and the question of whether LLMs represent, or merely mimic, a notion of evolving logical state. Our goal is not to draw hard boundaries, but to identify where the current limits lie, and how they might be extended.

• The paper evaluates the trade-offs between LLM-based informal reasoning and the strict requirements of formal mathematics.
• It details LLM training pipelines—including fine-tuning, reward modeling, and iterative inference—yielding up to 80% accuracy on benchmarks like miniF2F.
• The survey highlights challenges in autoformalization and state representation, advocating for declarative proofs and external tool integration.

Mathematical Reasoning in the Age of LLMs: A Technical Analysis

Introduction

The paper "Thinking Machines: Mathematical Reasoning in the Age of LLMs" (2508.00459) presents a comprehensive survey and critical analysis of the intersection between LLMs and mathematical reasoning, with a particular focus on the dichotomy between informal and formal mathematics. The authors systematically dissect the technical, methodological, and epistemological challenges that arise when deploying LLMs for mathematical problem solving and theorem proving, and provide a detailed comparative paper of recent models, datasets, and benchmarks. The work is notable for its rigorous treatment of the trade-offs between informal and formal mathematical domains, the brittleness of proof generation compared to code synthesis, and the question of whether LLMs internally represent computational or deductive state.

Formal vs. Informal Mathematics: Technical Foundations

The distinction between informal and formal mathematics is foundational to the paper's analysis. Informal mathematics, as encountered in textbooks and research articles, is characterized by natural language exposition interleaved with symbolic notation, logical connectives, and argumentative indicators. The lack of a fixed set of logical rules and explicit axioms renders informal proofs non-mechanizable, requiring human interpretation for validation. In contrast, formal mathematics, as instantiated in proof assistants (e.g., Lean, Isabelle, Mizar), is governed by explicit symbolic languages, finite rule sets, and mechanizable verification. The mechanization of mathematics, as noted by Gödel, enables the highest degree of exactness, but at the cost of increased proof length and complexity (de Bruijn factor).

This dichotomy has profound implications for LLM training and deployment. Informal mathematics aligns well with the statistical and linguistic modeling capabilities of LLMs, while formal mathematics demands syntactic precision and logical rigor that are challenging for autoregressive models trained primarily on natural language corpora.

LLM Training Pipelines and Reasoning Behavior

The paper provides a detailed breakdown of the LLM training pipeline, emphasizing the transition from linguistic modeling (pretraining) to cognitive modeling (fine-tuning, RLHF, inference-time scaling). Pretraining on large-scale text corpora imparts domain-agnostic linguistic competence, but subsequent stages (SFT, reward model training, RL) are critical for aligning models with task-specific reasoning objectives.

Supervised fine-tuning on curated mathematical datasets (e.g., DeepSeek-Prover, Minerva) enables models to learn the structure and flow of mathematical arguments and formal proofs. Reward model training and RL introduce qualitative feedback mechanisms, often leveraging human preferences or proxy evaluators, to guide model behavior in symbolic domains. Inference-time scaling techniques (massive sampling, reranking, iterative inference, tool use) further enhance performance by exploiting computational resources at test time.

The authors highlight the importance of meta-cognitive prompting (e.g., "Let's think this through") and chain-of-thought (CoT) reasoning, which have become mainstream strategies for eliciting structured, multi-step reasoning from LLMs.

Datasets and Benchmarks: Evaluating Mathematical Reasoning

A central contribution of the paper is its survey of recent datasets and benchmarks for mathematical reasoning, including AIME 2024, PGPS9K, miniF2F, and FrontierMath. These datasets span a spectrum from high school competition problems (AIME) to multimodal geometry (PGPS9K), formalized olympiad-level mathematics (miniF2F), and advanced, unpublished research-level problems (FrontierMath).

Performance on these benchmarks is driven by both general-purpose LLMs (e.g., OpenAI o1/o3, Claude 3.5) and math-specific models (e.g., DeepSeek-R1, Kimina-Prover, GOLD). Notably, DeepSeek-R1 achieves 79.8% accuracy on AIME 2024, while Kimina-Prover attains 80.7% pass@8192 on miniF2F. However, even state-of-the-art models struggle with the complexity of FrontierMath, with OpenAI's o3 solving only 25.2% of problems.

Figure 1: A sequence of progressive changes proposed by AlphaEvolve to discover faster matrix multiplication algorithms. The smooth search space facilitates incremental improvement.

The inclusion of visual reasoning (PGPS9K) and the challenge of data contamination (FrontierMath) underscore the evolving landscape of mathematical AI evaluation.

Comparative Analysis: Informal vs. Formal Reasoning Systems

The paper presents a rigorous comparative analysis of informal and formal mathematical reasoning systems. Informal reasoning tasks typically involve generating full arguments in natural language, leveraging chain-of-thought prompting and postprocessing techniques (sampling, reranking, tool-augmented reasoning). Formal reasoning tasks, in contrast, are characterized by step-wise tactic generation, tight integration with proof assistants, and iterative feedback loops.

The authors provide detailed tables comparing model architectures, training strategies, context representation, premise retrieval, and feedback mechanisms across leading systems (Minerva, DeepSeek-R1, Kimina-Prover, Lyra). The brittleness of formal proof generation is attributed to the all-or-nothing nature of logical correctness, sparse and binary feedback, and the difficulty of recovering from invalid tactics.

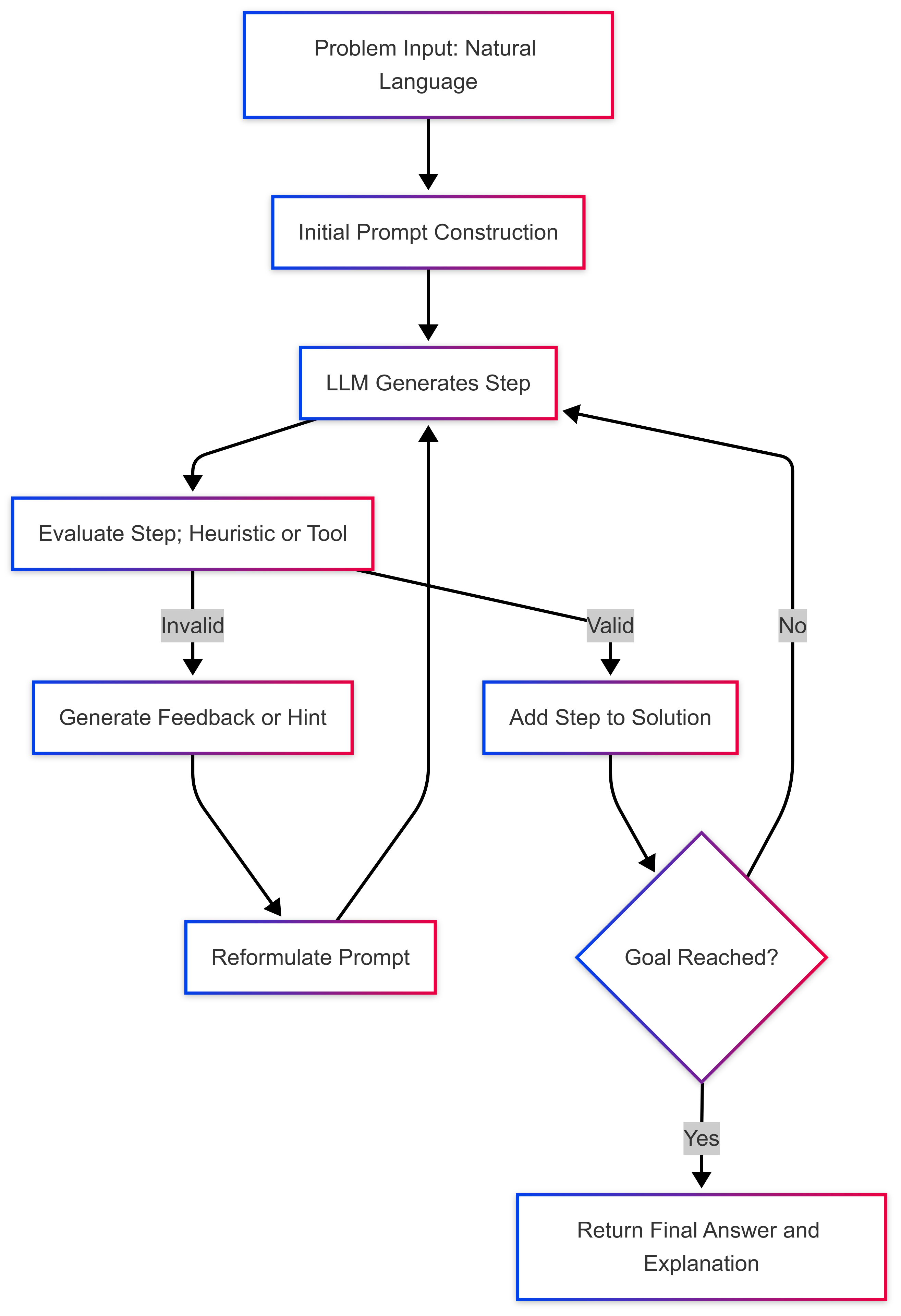
Figure 2: Typical interaction loop between a formal prover and a LLM is the case of formal mathematics.

The analysis highlights the limitations of procedural proof styles and advocates for the adoption of declarative proof styles, which align more closely with chain-of-thought reasoning and facilitate coarser, semantically meaningful steps.

Autoformalization: Bridging Informal and Formal Mathematics

Autoformalization—the automatic translation of informal mathematical text into formal specifications and proofs—is identified as a critical bridge between human mathematical practice and machine verification. Early neural network approaches relied on artificially generated corpora and seq2seq architectures, achieving moderate success. Recent work leverages LLMs (PaLM, Codex, GPT-4o, Llama3, DeepSeek-Math) and human-authored datasets (miniF2F, Def_Wiki, Def_ArXiv), with BLEU scores and manual analysis indicating incremental improvements.

The autoformalization of definitions and statements remains challenging, with models struggling to align informal language with formal constructs and external libraries. Structured refinement and definition grounding strategies yield notable improvements, but the semantic gap persists.

For proofs, two-stage approaches (e.g., Codex generating formal proof sketches, followed by automated theorem provers completing the details) have demonstrated measurable gains in proof success rates. However, the process is brittle, sensitive to dataset structure, and limited by the lack of step-level supervision and semantic feedback.

Major Questions and Theoretical Implications

The paper addresses three central questions:

1. Are LLMs more naturally suited to learning formal or informal mathematics? Informal mathematics is more amenable to LLMs due to its narrative structure, linguistic accessibility, and smooth error landscape. Formal mathematics, with its syntactic rigidity and brittle error surface, poses significant challenges for autoregressive models.
2. Why is proving harder than coding? The error landscape for code synthesis is smoother, with partial correctness, localizable errors, and redundant patterns facilitating recovery and learning. Formal proof generation is brittle, with single errors derailing the entire proof trajectory and sparse feedback limiting exploration.
3. Do LLMs possess a notion of computational state? LLMs exhibit only implicit state tracking, relying on statistical pattern recognition rather than explicit simulation or deductive state representation. This suffices for code generation and informal reasoning, but fails in formal domains where precise state management is essential.

The authors further analyze iterative proof, search, and revision loops, distinguishing between interactive revision (multi-turn exchanges with external evaluators) and intra-pass self-correction (embedded verification within a single generation pass). Both paradigms face limitations in scalability, feedback granularity, and integration with formal toolchains.

Future Directions and Open Challenges

The paper identifies several avenues for future research:

• Declarative Proof Styles: Transitioning from procedural to declarative proof writing to better align with LLM capabilities and facilitate coarse-grained reasoning.
• Forward vs. Backward Reasoning: Teaching models to flexibly switch between reasoning directions, enabling hierarchical decomposition and improved interpretability.
• Benchmark Design: Developing epistemically robust benchmarks that capture the complexity and diversity of mathematical reasoning, including open problems and conjectures.
• Integration of External Tools: Enhancing LLMs with tool-augmented reasoning, semantic retrieval, and modular agent architectures to overcome limitations in state tracking and feedback.
• Epistemological Considerations: Addressing the role of formalization in mathematical understanding, confidence, and human-machine interaction.

Conclusion

The paper provides a technically rigorous and nuanced analysis of the current state and future prospects of mathematical reasoning with LLMs. Informal mathematics remains the most accessible domain for LLMs, while formal mathematics and interactive theorem proving expose fundamental limitations in model architecture, training, and feedback. The integration of LLMs into formal reasoning systems demands a rethinking of representation, interaction paradigms, and proof style, with declarative approaches and flexible reasoning directions offering promising pathways. The challenges of autoformalization, error recovery, and state representation underscore the need for continued research at the intersection of AI, logic, and mathematical practice. The work sets a high standard for future investigations into the cognitive and epistemological dimensions of machine reasoning in mathematics.