Dual Riemannian Newton Method on Statistical Manifolds (2511.11318v1)

Abstract: In probabilistic modeling, parameter estimation is commonly formulated as a minimization problem on a parameter manifold. Optimization in such spaces requires geometry-aware methods that respect the underlying information structure. While the natural gradient leverages the Fisher information metric as a form of Riemannian gradient descent, it remains a first-order method and often exhibits slow convergence near optimal solutions. Existing second-order manifold algorithms typically rely on the Levi-Civita connection, thus overlooking the dual-connection structure that is central to information geometry. We propose the dual Riemannian Newton method, a Newton-type optimization algorithm on manifolds endowed with a metric and a pair of dual affine connections. The dual Riemannian Newton method explicates how duality shapes second-order updates: when the retraction (a local surrogate of the exponential map) is defined by one connection, the associated Newton equation is posed with its dual. We establish local quadratic convergence and validate the theory with experiments on representative statistical models. Thus, the dual Riemannian Newton method thus delivers second-order efficiency while remaining compatible with the dual structures that underlie modern information-geometric learning and inference.

• The paper introduces the dual Riemannian Newton method that exploits dual affine connections for quadratic convergence on statistical manifolds.
• The paper shows that on dually flat manifolds, the method reduces to classical Euclidean Newton steps, significantly speeding up convergence compared to first-order methods.
• The paper validates the approach on models including log-linear, Gaussian divergence minimization, and Beta mixtures, demonstrating its practical efficiency over traditional optimizers.

Dual Riemannian Newton Method for Statistical Manifolds: Theory, Algorithms, and Empirical Analysis

Introduction and Theoretical Foundation

This paper introduces the dual Riemannian Newton method—an optimization framework designed for statistical manifolds endowed with a Riemannian metric and an arbitrary pair of dual affine connections, a structure central to information geometry. The motivation arises from the inadequacy of first-order methods, such as natural gradient descent, to achieve rapid local convergence, especially on curved parameter spaces of probabilistic models. Traditional second-order Riemannian optimization typically employs the Levi-Civita connection exclusively, thus failing to exploit the full dualistic structure that characterizes information geometry.

The dual Riemannian Newton method generalizes Newton-type updates by exploiting both the chosen connection $\nabla$ and its dual $\nabla^*$. The core theoretical insight posits that, for a second-order retraction defined by $\nabla$, the associated Newton equation must be solved with respect to $\nabla^*$. The paper formalizes the geometric, coordinate-free ascent to a quadratic local approximation, aligning Taylor expansions in manifold coordinates with dual-affine Hessians, and rigorously proves local quadratic convergence.

Dual Riemannian Newton Algorithm

The algorithm operates by iteratively solving, at each point $p$ on the manifold, a Newton equation of the form:

$$\mathrm{Hess}^* f(p)[X_p] = -\operatorname{grad} f(p)$$

before retracting along $X_p$ using a suitable second-order retraction compatible with the chosen connection. This dual update structure leverages the torsion-free and duality properties inherent to the pair $(\nabla, \nabla^*)$.

On dually flat manifolds—statistical manifolds whose $\nabla$ and $\nabla^*$ connections are both flat—the method reduces, in appropriate affine coordinates, to classical Euclidean Newton steps. The paper proves that, in such coordinates, each dual Riemannian Newton iteration coincides with an ordinary Hessian inverse-gradient update, and establishes equivalence with the natural gradient method on certain canonical projection problems.

Algorithmic Implementation and Coordinate Analysis

The authors provide explicit coordinate-based algorithms for both the dual Riemannian Newton and natural gradient methods. The dual method requires computation of Christoffel symbols for both $\nabla$ and $\nabla^*$; for the popular case of $\alpha$-connections, these quantities are well characterized in information geometry and can be efficiently calculated for exponential family models and other common statistical models.

The dual Riemannian Newton update incorporates local curvature in a more geometrically correct fashion than first-order methods and is computationally tractable via local coordinate charts. The update step is shown to coincide with the mirror descent method only for unregularized projection problems on dually flat submanifolds; in the presence of regularization, the update departs from both natural gradient and mirror descent, adopting a genuinely second-order geometry-aware direction.

Quadratic Convergence Analysis

The paper rigorously proves local quadratic convergence of the dual Riemannian Newton method under strong regularity (positive-definiteness of the dual Hessian at the optimum). The argument utilizes properties of consistent matrix norms, the smoothness of the dual Hessian and retraction mappings, and bounds the deviation of the local quadratic model, establishing that in a sufficiently small neighborhood around any nondegenerate optimum, the next iterate converges quadratically.

Experimental Validation

The algorithm is empirically validated on three main model classes:

1. Log-linear Models with Higher-order Interactions

The dual Riemannian Newton method is applied to regularized maximum likelihood estimation in log-linear models with both first- and higher-order interaction terms. The experiments show that the method requires markedly fewer iterations to convergence compared to the natural gradient, mirror descent, and Adam optimizers, with total runtimes orders of magnitude lower. The convergence rate is influenced by the choice of $\alpha$-connection; $\alpha=1$ achieves the fastest convergence, aligning with the reduction to the Euclidean Newton method predicted by theory.

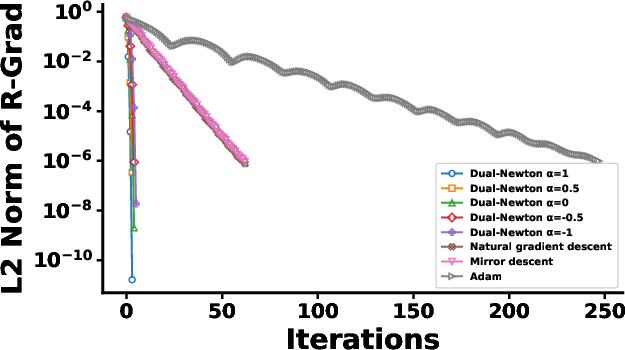
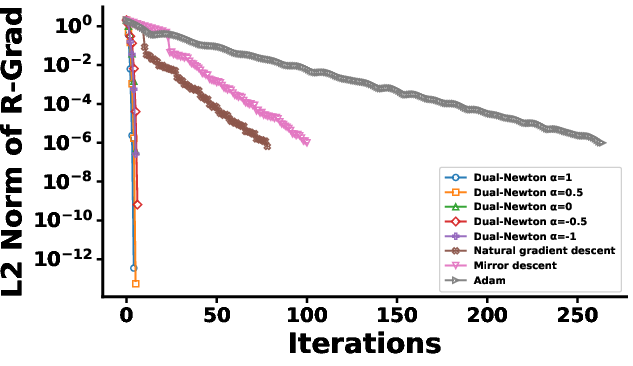
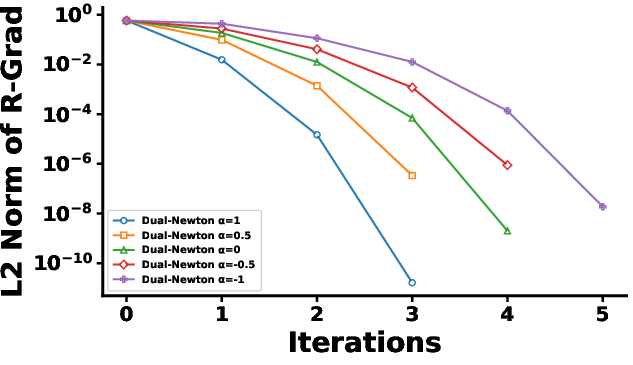
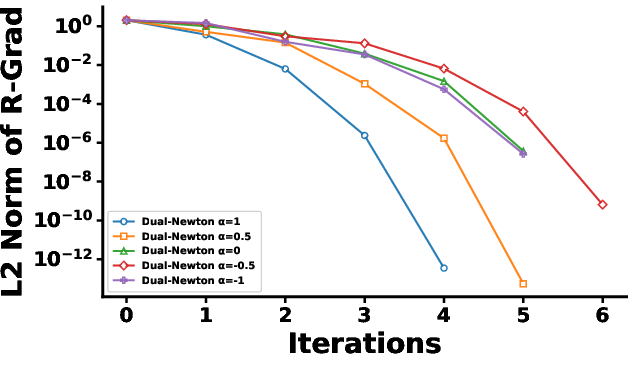
Figure 1: Number of iterations to convergence for each method under two regularization scenarios; the bottom row magnifies early Dual Riemannian Newton steps for clarity.

2. $\alpha$-Divergence Minimization for Gaussian Models

A projection-type problem using $\alpha$-divergence between general Gaussians demonstrates the method's flexibility beyond exponential families. Again, the dual Riemannian Newton algorithm converges within 10–13 steps, an order of magnitude faster than its first-order competitors. Optimization paths confirm that the dual Newton steps cut sharply through the parameter space, rather than following the tortuous trajectory characteristic of natural gradient or Adam.

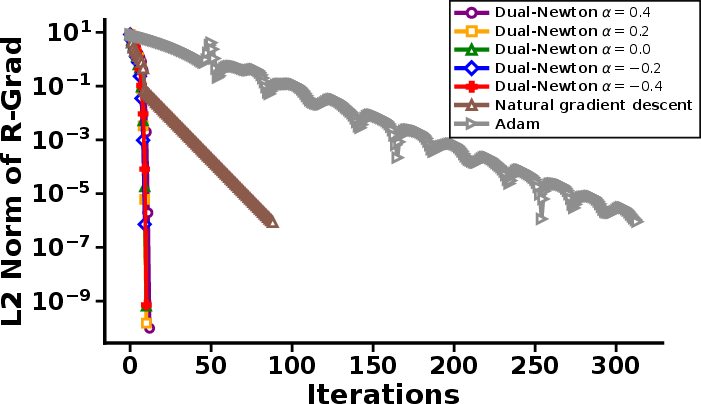
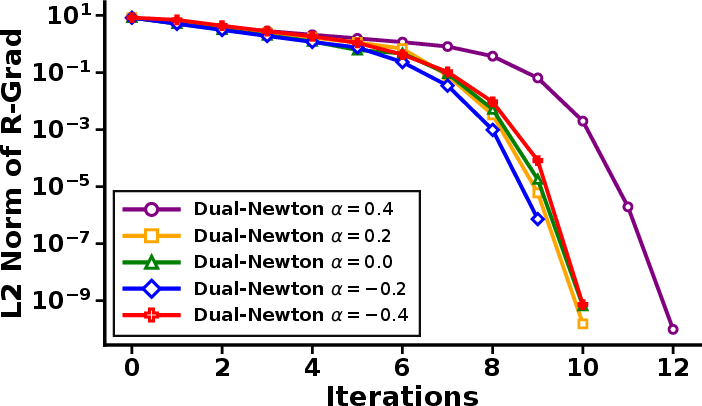
Figure 2: Left—decay of the Riemannian gradient norm across methods; Right—a zoom-in illustrating the rapid early convergence of the dual Riemannian Newton scheme.

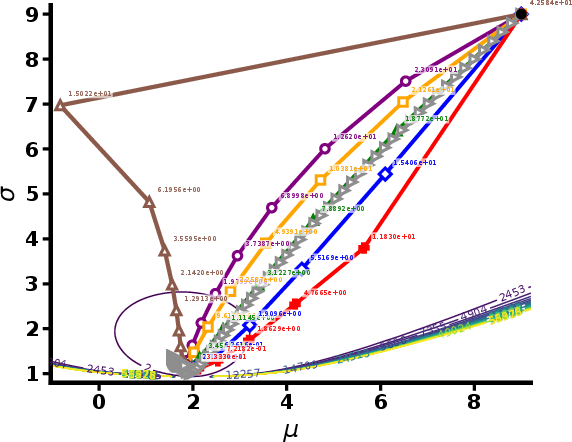
Figure 3: Visualization of trajectory paths for each method; numbers indicate the $\alpha$-divergence at each shown step.

3. Beta Mixture Model Maximum Likelihood

To demonstrate generalizability to non-exponential families, Beta mixture models are fit by maximizing the log-likelihood over mixture parameters. The dual Riemannian Newton procedure again displays strong local convergence—fewer than 8 iterations, versus hundreds or thousands for baseline methods.

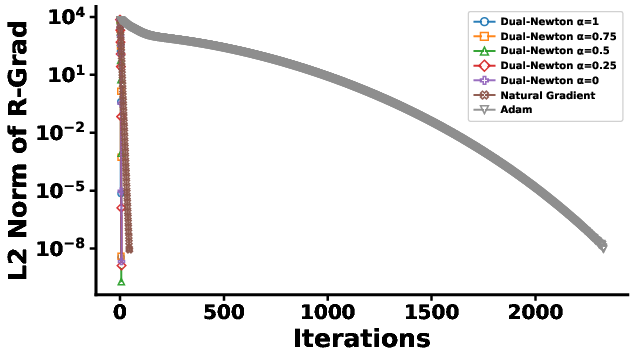
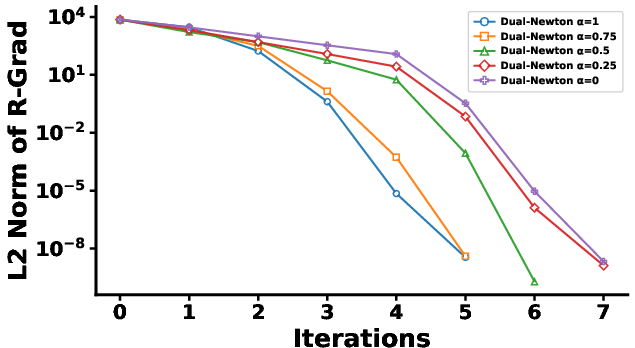
Figure 4: Left—iterative Riemannian gradient norm for each method; Right—magnification of early dual Riemannian Newton steps, underscoring rapid convergence.

Descent Properties, $\alpha$-Connection Choices, and Geodesic Convexity

A key theoretical contribution is the clarification of the relationship between the choice of affine connection, the positive-definiteness of the dual Hessian, and the descent property of the Newton update. The notion of $\alpha$-geodesic strict convexity is introduced: only for certain $\alpha$ does the objective function remain strictly convex along $\alpha$-geodesics, ensuring every Newton step is a descent step. Empirical evidence is provided showing that for $\alpha=1$ (the exponential connection) and canonical Kullback-Leibler objectives, this property holds generically, while for other $\alpha$-values it may fail.

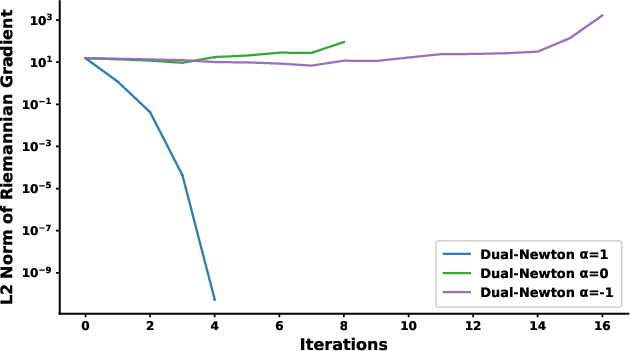
Figure 5: Riemannian gradient norm evolution under various $\alpha$ connections, illustrating that all steps are descent steps when $\alpha=1$.

Implications and Future Directions

The dual Riemannian Newton method provides an algorithmic framework that is both geometrically principled and computationally practical for a wide variety of statistical inference problems. The method achieves second-order efficiency while respecting the dual structure of information geometry, offering both theoretical guarantees (quadratic convergence) and empirical superiority for a class of important models.

Potential implications include improved optimization in high-dimensional probabilistic modeling, more robust second-order variational inference algorithms, and new avenues in manifold-based learning where dual connections encode prior geometric knowledge. Future directions could involve adaptive selection of the optimal dual connection per iteration, extensions to stochastic and online settings, and integration into scalable neural network training pipelines where the information-geometric structure of parameter spaces is nontrivial.

Conclusion

The dual Riemannian Newton method advances optimization on statistical manifolds by integrating manifold metric structure and dual connection geometry. The approach consolidates and extends both information geometric theory and second-order optimization practice. By establishing a formal connection between dual affine geometry and superlinear convergence, and demonstrating empirical gains over both first-order Riemannian and classical Euclidean optimizers, this work lays a strong foundation for further research at the intersection of information geometry, optimization, and modern statistical learning.