Information Geometry of Variational Bayes (2509.15641v1)

Abstract: We highlight a fundamental connection between information geometry and variational Bayes (VB) and discuss its consequences for machine learning. Under certain conditions, a VB solution always requires estimation or computation of natural gradients. We show several consequences of this fact by using the natural-gradient descent algorithm of Khan and Rue (2023) called the Bayesian Learning Rule (BLR). These include (i) a simplification of Bayes' rule as addition of natural gradients, (ii) a generalization of quadratic surrogates used in gradient-based methods, and (iii) a large-scale implementation of VB algorithms for LLMs. Neither the connection nor its consequences are new but we further emphasize the common origins of the two fields of information geometry and Bayes with a hope to facilitate more work at the intersection of the two fields.

• The paper demonstrates that natural gradients, derived from Fisher information, are essential for optimal variational Bayes in exponential-family models.
• It introduces the Bayesian Learning Rule to efficiently compute these gradients, unifying natural-gradient descent with classical optimization methods.
• The study validates scalable implementations for large models like LLMs using the IVON algorithm, which matches or surpasses standard optimizers.

Information Geometry of Variational Bayes: A Technical Analysis

Introduction

The paper "Information Geometry of Variational Bayes" (2509.15641) provides a rigorous exposition of the intrinsic connection between information geometry and variational Bayes (VB), emphasizing the centrality of natural gradients in variational inference. The work systematically demonstrates that, for exponential-family posteriors, the computation or estimation of natural gradients is not merely beneficial but necessary for optimal VB solutions. The analysis extends to practical algorithmic consequences, including the Bayesian Learning Rule (BLR), the generalization of quadratic surrogates, and scalable implementations for large-scale models such as LLMs.

Variational Bayes and Information Geometry

The paper begins by formalizing the VB objective as an optimization over distributions, typically restricted to an exponential-family subset. The key insight is that, for exponential-family variational posteriors, the gradient of the entropy term with respect to the natural parameters is the Fisher information matrix. This leads to the optimality condition for the VB solution:

$$\lambda_* = \mathcal{I}(\lambda_*)^{-1} \nabla_{\lambda_*} \mathbb{E}_{q_{\lambda_*}}[-\ell(\theta)]$$

where $\lambda$ denotes the natural parameters, $\mathcal{I}(\lambda)$ is the Fisher information, and $\ell(\theta)$ is the loss. This result establishes that the natural gradient (Fisher-preconditioned gradient) is fundamental to VB, and any algorithm that ignores this geometry is inherently suboptimal in terms of convergence and solution quality.

The Bayesian Learning Rule and Dual Parameterization

The BLR is presented as a natural-gradient descent algorithm in the expectation parameter space, exploiting the duality between natural and expectation parameters in exponential families. The update in the expectation parameter space is equivalent to a vanilla gradient step, but in the natural parameter space, it corresponds to a natural gradient step. The BLR update is:

$$\mu_{t+1} \leftarrow (1-\rho_t)\mu_t + \rho_t \nabla_{\mu_t} \mathbb{E}_{q_{\mu_t}}[-\ell(\theta)]$$

where $\mu$ is the expectation parameter and $\rho_t$ is the learning rate. This formulation avoids explicit inversion of the Fisher matrix and is computationally efficient.

Bayes' Rule as Addition of Natural Gradients

A central theoretical contribution is the reinterpretation of Bayes' rule for conjugate exponential-family models as the addition of natural gradients. For such models, the posterior natural parameter is simply the sum of the prior and likelihood natural parameters:

$$\lambda_* = \lambda_{\text{lik}} + \lambda_{\text{prior}}$$

The paper formalizes that, in these cases, the natural gradient of the expected log-likelihood and log-prior are exactly the respective natural parameters. Consequently, a single BLR step with $\rho_t=1$ recovers the exact posterior, demonstrating that Bayes' rule is a special case of natural-gradient descent.

Generalization of Quadratic Surrogates

The BLR framework generalizes the quadratic surrogates used in Newton and quasi-Newton optimization methods. The BLR surrogate is a mirror-descent step in the expectation parameter space, with the KL divergence as the Bregman divergence. For Gaussian variational families, the BLR surrogate reduces to a global quadratic surrogate, where the gradient and Hessian are averaged over the variational distribution, not just evaluated at the mean. This yields a more global approximation than the local Taylor expansion used in Newton's method. The quadratic surrogate of Newton's method is recovered as a limiting case of the BLR surrogate under the delta method approximation.

Scalable Variational Bayes for Large Models

A significant practical contribution is the demonstration that natural-gradient VB can be implemented at scale for large models, including LLMs. The paper shows that the BLR update for diagonal-covariance Gaussian variational families closely resembles the RMSprop/Adam optimizer, with the key difference being the use of the Hessian (or its diagonal) and expectations over the variational distribution. The IVON algorithm, a Riemannian extension of the BLR, is shown to be computationally competitive with Adam, with only minor overhead due to sampling and Hessian estimation.

Figure 1: Pseudo-code comparison of RMSprop/Adam and IVON, highlighting the correspondence and differences in the update rules, particularly the use of expectations and Hessian estimation in IVON.

Empirical results on GPT-2 (OpenWebText) and ResNet-50 (ImageNet) demonstrate that IVON matches or slightly outperforms AdamW in terms of accuracy and runtime, refuting the claim that natural-gradient methods are too computationally intensive for large-scale deep learning.

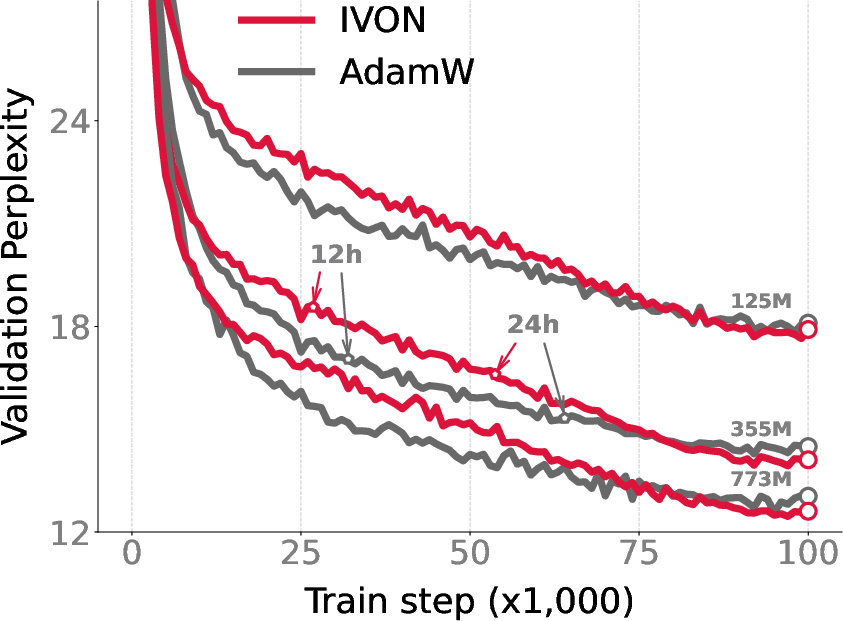
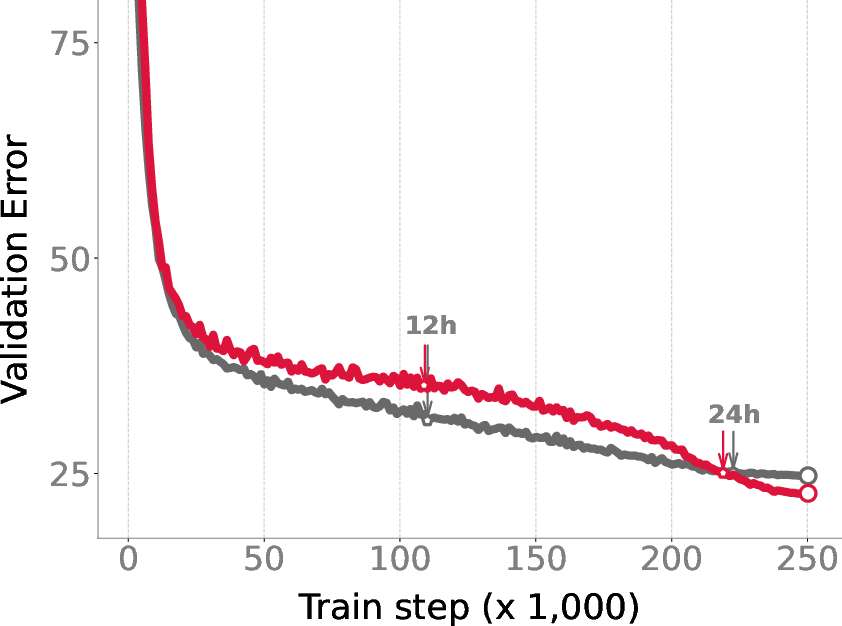
Figure 2: Training curves for GPT-2 and ResNet-50, showing comparable runtime and improved final accuracy for IVON relative to AdamW.

Theoretical and Practical Implications

The paper's analysis unifies several strands of research in variational inference, optimization, and information geometry. The necessity of natural gradients for VB in exponential families provides a theoretical foundation for the observed empirical benefits of natural-gradient methods. The reinterpretation of Bayes' rule as a natural-gradient update bridges Bayesian inference and optimization, suggesting new algorithmic strategies for both fields. The generalization of quadratic surrogates via BLR opens avenues for designing new optimization algorithms with better global properties.

On the practical side, the demonstration that natural-gradient VB can be implemented efficiently for large models removes a major barrier to the adoption of Bayesian methods in deep learning. The close correspondence between BLR/IVON and standard optimizers like Adam suggests that Bayesian learning can be integrated into existing deep learning pipelines with minimal overhead.

Conclusion

This work rigorously establishes the centrality of information geometry and natural gradients in variational Bayes, both theoretically and algorithmically. The necessity of natural gradients for optimal VB solutions in exponential families is demonstrated, and the BLR framework is shown to generalize and subsume classical optimization surrogates. The practical scalability of natural-gradient VB, as evidenced by the IVON algorithm's performance on large models, has significant implications for the future of Bayesian deep learning. The theoretical unification of Bayesian inference and optimization via information geometry is likely to inspire further research at this intersection, with potential impact on both the theory and practice of machine learning.