A unified physics-informed generative operator framework for general inverse problems (2511.03241v1)

Abstract: Solving inverse problems governed by partial differential equations (PDEs) is central to science and engineering, yet remains challenging when measurements are sparse, noisy, or when the underlying coefficients are high-dimensional or discontinuous. Existing deep learning approaches either require extensive labeled datasets or are limited to specific measurement types, often leading to failure in such regimes and restricting their practical applicability. Here, a novel generative neural operator framework, IGNO, is introduced to overcome these limitations. IGNO unifies the solution of inverse problems from both point measurements and operator-valued data without labeled training pairs. This framework encodes high-dimensional, potentially discontinuous coefficient fields into a low-dimensional latent space, which drives neural operator decoders to reconstruct both coefficients and PDE solutions. Training relies purely on physics constraints through PDE residuals, while inversion proceeds via efficient gradient-based optimization in latent space, accelerated by an a priori normalizing flow model. Across a diverse set of challenging inverse problems, including recovery of discontinuous coefficients from solution-based measurements and the EIT problem with operator-based measurements, IGNO consistently achieves accurate, stable, and scalable inversion even under severe noise. It consistently outperforms the state-of-the-art method under varying noise levels and demonstrates strong generalization to out-of-distribution targets. These results establish IGNO as a unified and powerful framework for tackling challenging inverse problems across computational science domains.

• The paper introduces IGNO, a generative neural operator framework that leverages structured latent representations to efficiently solve inverse problems governed by PDEs.
• The paper demonstrates IGNO's robust performance with lower RMSE and high cross-correlation in recovering both continuous and piecewise-constant coefficients under noisy conditions.
• The paper validates IGNO's unique ability to handle diverse measurement modalities, including operator-based EIT data, enabling accurate reconstructions across various applications.

A Unified Physics-Informed Generative Operator Framework for General Inverse Problems

This essay provides a comprehensive review of the paper "A Unified Physics-Informed Generative Operator Framework for General Inverse Problems" (2511.03241). The paper introduces IGNO, an innovative generative neural operator framework aimed at solving inverse problems governed by partial differential equations (PDEs). IGNO extends the capabilities of current deep learning techniques by addressing challenges related to sparse measurements, noise, high-dimensional parameters, and discontinuities. This framework is not bound by the requirements of labeled datasets and excels in generalizing across different types of measurement modalities with robust performance.

Introduction to Inverse Problems

Inverse problems are central in various scientific and engineering domains, necessitating the inference of unknown system properties from incomplete or indirect observations. Such problems, often described by PDEs, are inherently challenging due to their high dimensionality, ill-posed nature, and noise sensitivity. Traditional inversion methods involve computationally expensive iterative optimization constrained by PDEs. Machine learning methods have attempted to overcome these challenges, yet face constraints like the need for extensive labeled data or fixed measurement types.

The IGNO Framework

IGNO integrates the advantages of generative modeling, neural operator learning, and physics-informed machine learning to solve inverse problems efficiently. Key innovations include:

1. Generative Architecture: IGNO maps high-dimensional coefficient fields to low-dimensional latent representations, capitalizing on neural operator decoders to reconstruct coefficients and PDE solutions. This transformation facilitates efficient gradient-based optimization in latent space.
2. Physics-Informed Training: The framework relies solely on physics constraints through PDE residuals, bypassing the necessity for labeled training data pairs. This approach is purely self-supervised, leveraging the neural operator decoders' ability to predict across broad input families.
3. Measurement Generalization: A dual-encoder structure allows IGNO to process both solution-based and operator-valued measurement data within a single unified framework, managed by leveraging structured latent spaces.

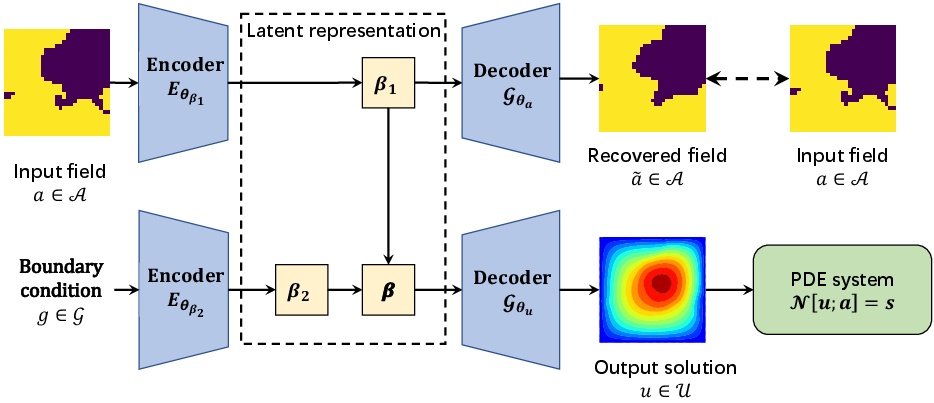
   Figure 1: The IGNO framework for PDE inverse problems. The generative neural operator architecture encodes the coefficient field $a$ and the boundary condition $g$ into a structured latent variable $\bm{\beta}$.

Numerical Results

Continuous Coefficient Recovery

The paper demonstrates IGNO's proficiency in recovering continuous permeability fields from sparse pressure measurements with added noise. IGNO results in significantly lower RMSE values compared to PI-DIONs, particularly under severe noise conditions, highlighting its robust performance.

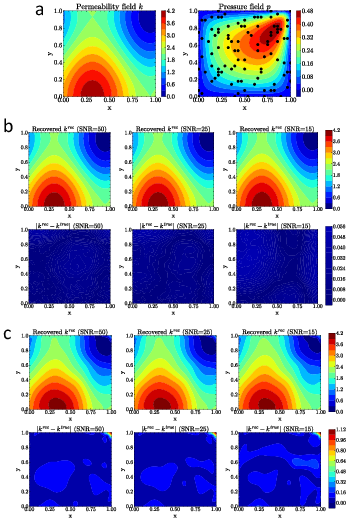
Figure 2: Recovery of continuous coefficients with solution-based measurements (In-distribution case): (a) the ground truth permeability field $k$ and the corresponding pressure field $p$ (black dots denote $m=100$ random sensors); (b) recovered permeability $k^{rec}$.

Discontinuous Coefficient Recovery

For piecewise-constant target coefficients, IGNO successfully reconstructs phase boundaries despite noise, achieving high cross-correlation indicators. Its probabilistic decoding approach overcomes the challenges associated with undefined gradients present in discontinuous fields.

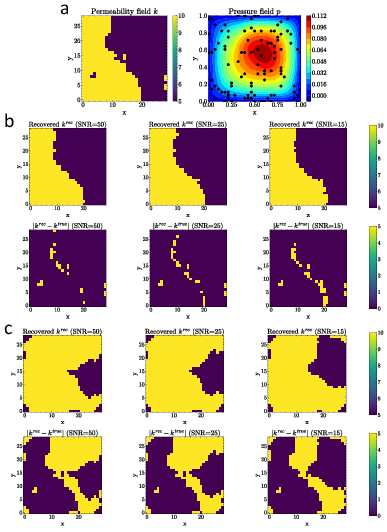
Figure 3: Recovery of piecewise-constant coefficients with solution-based measurements (In-distribution case): (a) the true permeability field $k$ and the corresponding pressure field $p$ (black dots denote $m=100$ random sensors); (b) recovered permeability $k^{rec}.

Electrical Impedance Tomography (EIT)

In tackling the EIT problem, where measurements are operator-based (DtN maps), IGNO uniquely accommodates such complex data without requiring repeated PDE solves. It achieves accurate reconstructions even against out-of-distribution changes, validating its flexibility and robustness.

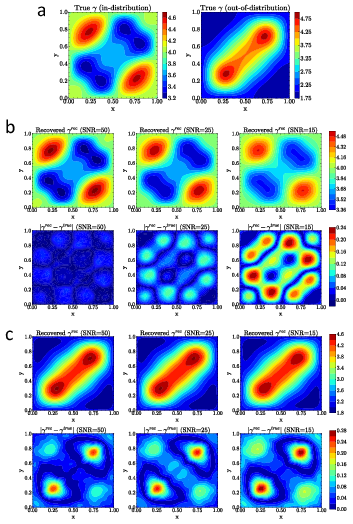
Figure 4: Performance of IGNO in solving the EIT problem: (a) the truth conductivity gamma in In-distribution (left) and Out-of-distribution (right) cases.

Implications and Future Directions

IGNO represents a significant advancement in solving general inverse problems with wide-ranging applications in geophysics, medical imaging, and materials science. Its ability to adapt to varied measurement types and conditions offers new opportunities to address complex inverse problems traditionally deemed intractable. Future work could enhance IGNO to incorporate probabilistic inversion methods for uncertainty quantification and extend its scalability for even higher-dimensional problems. Additionally, exploring adaptive or hierarchical latent space designs could further enhance performance for highly heterogeneous scenarios.

Conclusion

The paper presents IGNO as an effective, scalable, and versatile framework for resolving PDE-governed inverse problems, overcoming the limitations of previous methodologies by integrating structured latent representations, generative modeling, and physics-informed learning. Through comprehensive numerical results, IGNO is demonstrated as a leading approach, capable of efficient, accurate, and robust inversion across diverse scientific and engineering domains.