Probabilistic operator learning: generative modeling and uncertainty quantification for foundation models of differential equations (2509.05186v2)

Abstract: In-context operator networks (ICON) are a class of operator learning methods based on the novel architectures of foundation models. Trained on a diverse set of datasets of initial and boundary conditions paired with corresponding solutions to ordinary and partial differential equations (ODEs and PDEs), ICON learns to map example condition-solution pairs of a given differential equation to an approximation of its solution operator. Here, we present a probabilistic framework that reveals ICON as implicitly performing Bayesian inference, where it computes the mean of the posterior predictive distribution over solution operators conditioned on the provided context, i.e., example condition-solution pairs. The formalism of random differential equations provides the probabilistic framework for describing the tasks ICON accomplishes while also providing a basis for understanding other multi-operator learning methods. This probabilistic perspective provides a basis for extending ICON to \emph{generative} settings, where one can sample from the posterior predictive distribution of solution operators. The generative formulation of ICON (GenICON) captures the underlying uncertainty in the solution operator, which enables principled uncertainty quantification in the solution predictions in operator learning.

• The paper presents a rigorous probabilistic framework where ICON implicitly performs Bayesian inference and GenICON quantifies uncertainty in differential equation models.
• The methodology uses random differential equations in infinite-dimensional spaces to establish robustness for both forward and inverse problems.
• The framework leverages GAN-based, transformer architectures to ensure accurate predictions even with noisy or partial data, enhancing scientific machine learning.

Probabilistic Operator Learning: Generative Modeling and Uncertainty Quantification for Foundation Models of Differential Equations

Introduction

This paper presents a rigorous probabilistic framework for operator learning, focusing on in-context operator networks (ICON) and their generative extension (GenICON) for ordinary and partial differential equations (ODEs/PDEs). The authors formalize the data-generating process for operator learning using random differential equations (RDEs), enabling a unified treatment of both forward and inverse problems. ICON is shown to implicitly perform Bayesian inference, approximating the mean of the posterior predictive distribution over solution operators conditioned on context. The generative extension, GenICON, enables sampling from the posterior predictive, providing principled uncertainty quantification. The framework is developed in infinite-dimensional Banach and Hilbert spaces, which is essential for scientific machine learning applications involving function-valued data.

Random Differential Equations as a Foundation for Operator Learning

The paper introduces RDEs as the mathematical basis for modeling the data-generating process in operator learning. RDEs generalize classical differential equations by treating parameters, initial/boundary conditions, and source terms as random variables in separable Banach or Hilbert spaces. This formalism naturally induces probability measures on function spaces, which are essential for understanding the statistical properties of operator learning models.

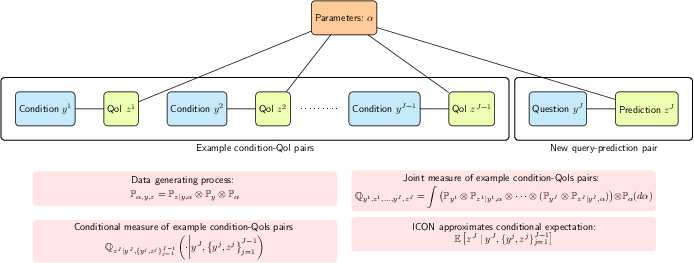
Figure 1: The ICON graphical model, corresponding to the probability measure described in the joint parameter-example context.

The RDE framework is applied to various classes of problems:

• Random ODEs: Parameters and initial conditions are random, and the solution is a stochastic process in $L^2$.
• Random Boundary Value Problems: Coefficients and boundary data are random, with solutions in $L^2$ over the domain and boundary.
• Random PDEs: Flux functions and initial data are random, with solutions in $BV$ or $L^2$ spaces.

This probabilistic perspective enables the characterization of joint and conditional distributions over parameters, conditions, and solutions, forming the basis for subsequent Bayesian analysis.

Probabilistic Formulation of In-Context Operator Learning

ICON is formalized as a mapping from a set of example condition-QoI pairs and a new condition to a predicted QoI. The training objective is a least-squares regression over the joint distribution of example pairs, which, in the infinite-dimensional setting, is shown to approximate the conditional expectation of the posterior predictive distribution.

The key theoretical result is that ICON's regression objective yields the unique $L^2$-optimal estimator for the conditional expectation of the QoI given context. This holds for both forward and inverse problems, regardless of identifiability, and is robust to partial or noisy observations.

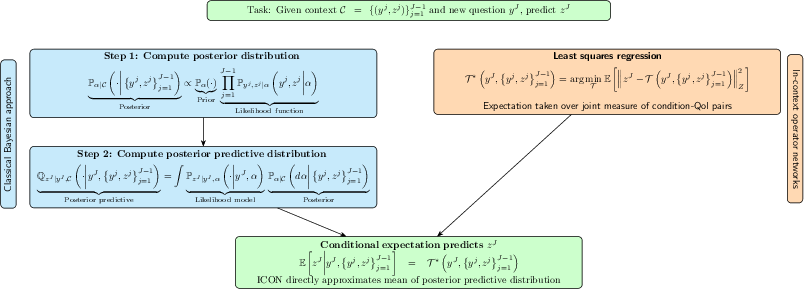
Figure 2: ICON performs Bayesian inference by directly approximating the mean of the posterior predictive distribution, bypassing explicit posterior computation.

The Bayesian interpretation is made explicit: ICON implicitly infers the latent operator parameters from context and applies the learned operator to new conditions. The prior and likelihood are implicitly encoded in the training data, making ICON a likelihood-free, amortized inference method. The framework is agnostic to the choice of latent variables, as long as the posterior predictive is correctly characterized.

Generative ICON: Sampling and Uncertainty Quantification

The generative extension, GenICON, is constructed as a conditional generative model that samples from the posterior predictive distribution. The existence of such a model is established for infinite-dimensional Banach spaces using measure-theoretic arguments. GenICON enables uncertainty quantification by producing empirical distributions over predicted QoIs, from which moments and credible intervals can be estimated.

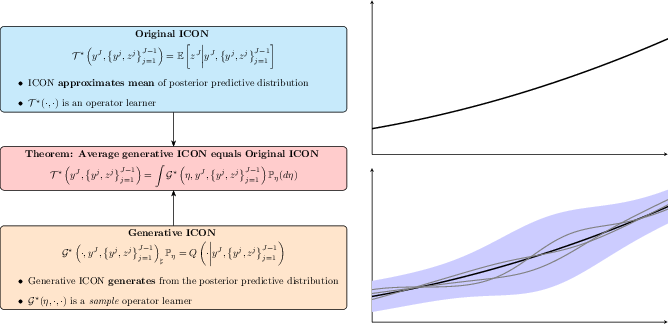
Figure 3: Standard ICON returns a single solution (mean of the posterior predictive), while GenICON samples the full posterior predictive, enabling uncertainty quantification.

The paper details a practical implementation using GANs with transformer-based architectures. The generator maps reference noise and context to predicted QoIs, while the discriminator enforces fidelity to the target conditional distribution via $(f,\Gamma)$-divergences and Lipschitz regularization. The training objective is designed to be robust to mutual singularity and mode collapse, and the architecture is scalable to high-dimensional function spaces.

Numerical Experiments

The authors present several numerical experiments demonstrating the robustness and capabilities of ICON and GenICON:

• Non-identifiability and Degenerate Posteriors: ICON is shown to produce accurate predictions even when the underlying operator parameters are non-identifiable, as the posterior predictive mean remains well-defined. Empirical errors are consistently low for both forward and inverse problems, regardless of identifiability.

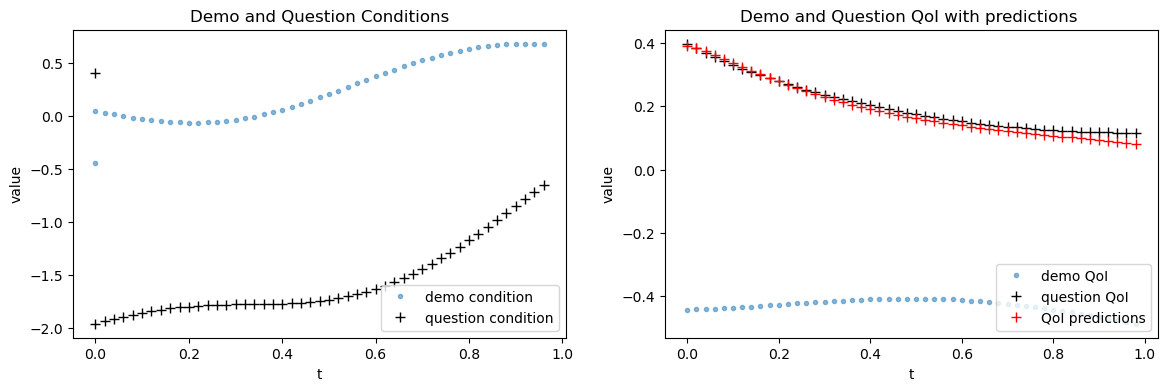
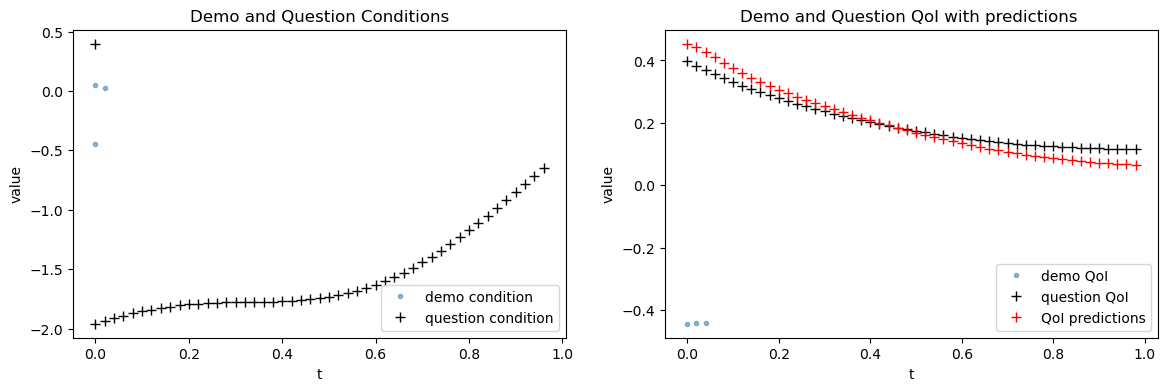
Figure 4: ICON accurately recovers ODE behavior with a single example condition-QoI pair, even with extremely short demos.

• Partial and Noisy Observations: ICON is robust to partial and noisy data, producing denoised predictions by leveraging the conditional expectation property. Empirical errors decrease with more context, and the model generalizes across heterogeneous observation patterns.

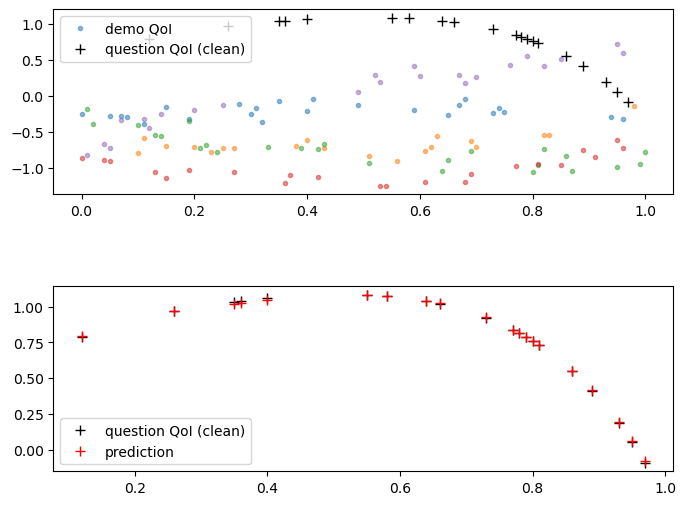
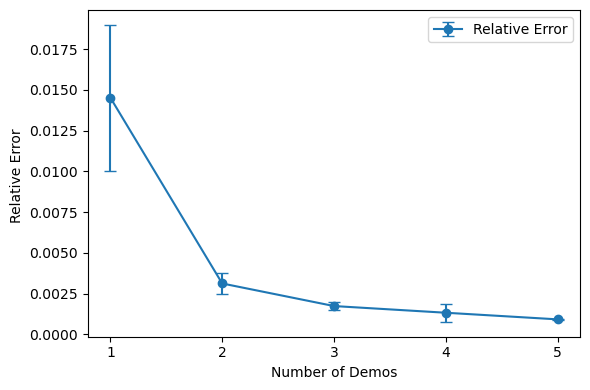
Figure 5: Visualization of ICON predictions for reaction-diffusion tasks with noisy QoIs, showing alignment with noise-free solutions.

• Generative ICON for Uncertainty Quantification: GenICON is trained on elliptic PDEs with varying noise levels and random boundary conditions. The model accurately recovers both the mean and variance of the posterior predictive, with empirical variances matching the prescribed noise levels. GenICON captures operator uncertainty due to random boundary conditions, producing diverse solution samples consistent with the underlying physics.

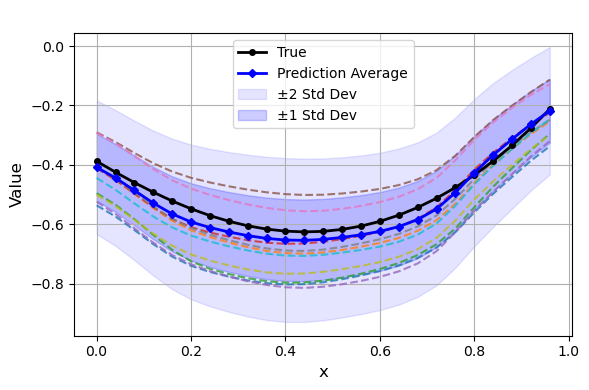
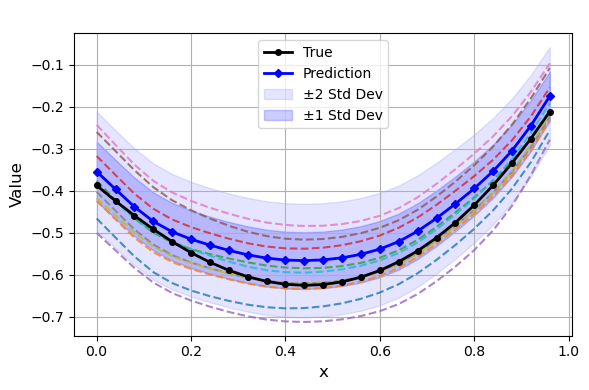
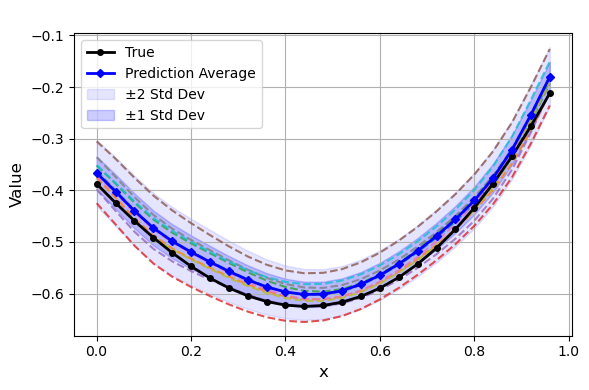
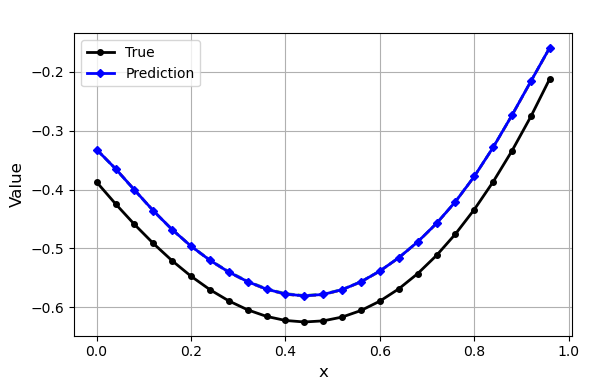
Figure 6: GenICON posterior predictive samples for $\sigma = 0.1$, showing calibrated uncertainty bands.

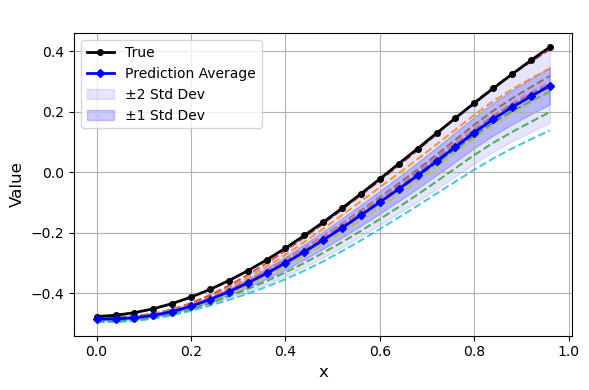
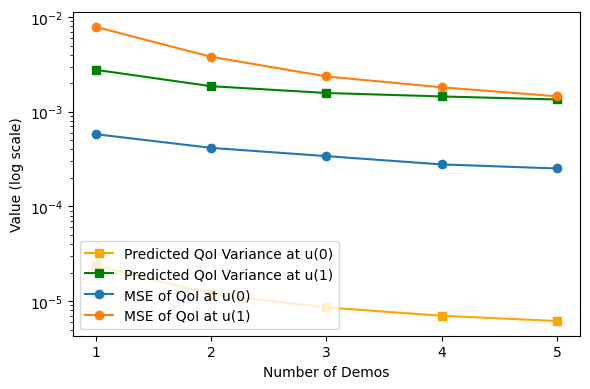
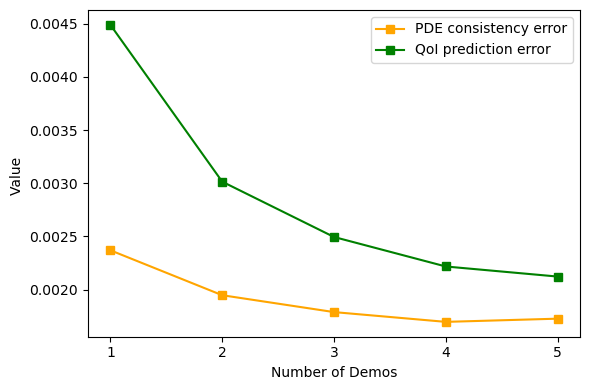
Figure 7: Example of QoI predictions for elliptic PDEs with random right boundary, illustrating GenICON's ability to capture output diversity.

Theoretical and Practical Implications

The probabilistic operator learning framework provides a rigorous foundation for understanding and extending operator learning methods, including multi-operator and foundation models. The Bayesian perspective explains ICON's robustness to non-identifiability, noise, and partial observations, and enables principled uncertainty quantification via generative modeling. The infinite-dimensional setting is essential for scientific applications, and the framework is compatible with advanced neural architectures and generative modeling techniques.

The generative extension (GenICON) is particularly relevant for applications requiring predictive uncertainty, such as inverse problems, model calibration, and scientific discovery. The existence theorem for conditional generative models in infinite dimensions is a significant theoretical contribution, with implications for future work in probabilistic scientific machine learning.

Conclusion

The paper establishes a comprehensive probabilistic framework for operator learning, demonstrating that ICON implicitly performs Bayesian inference and that its generative extension (GenICON) enables uncertainty quantification in infinite-dimensional settings. The framework is robust to non-identifiability, noise, and partial observations, and is compatible with modern neural architectures. Future directions include quantifying approximation errors in GenICON, exploring mode-seeking generative models, developing structure-preserving architectures, and extending the probabilistic formalism to other foundation models for differential equations. The results provide a principled basis for trustworthy and scalable scientific machine learning.