What Really Matters in Matrix-Whitening Optimizers? (2510.25000v1)
Abstract: A range of recent optimizers have emerged that approximate the same "matrix-whitening" transformation in various ways. In this work, we systematically deconstruct such optimizers, aiming to disentangle the key components that explain performance. Across tuned hyperparameters across the board, all flavors of matrix-whitening methods reliably outperform elementwise counterparts, such as Adam. Matrix-whitening is often related to spectral descent -- however, experiments reveal that performance gains are not explained solely by accurate spectral normalization -- particularly, SOAP displays the largest per-step gain, even though Muon more accurately descends along the steepest spectral descent direction. Instead, we argue that matrix-whitening serves two purposes, and the variance adaptation component of matrix-whitening is the overlooked ingredient explaining this performance gap. Experiments show that variance-adapted versions of optimizers consistently outperform their sign-descent counterparts, including an adaptive version of Muon. We further ablate variance adaptation strategies, finding that while lookahead style approximations are not as effective, low-rank variance estimators can effectively reduce memory costs without a performance loss.
Summary
- The paper demonstrates that matrix-whitening optimizers reduce training steps to 66–83% of Adam’s steps, highlighting superior efficiency over elementwise methods.
- It reveals that accurate spectral normalization is insufficient alone, with variance adaptation emerging as the key ingredient for performance improvement.
- The study offers practical insights on trade-offs, suggesting selective preconditioning and low-rank variance techniques to balance computational cost and memory usage.
Deconstructing Matrix-Whitening Optimizers: Spectral Normalization and Variance Adaptation
Introduction
This paper presents a systematic empirical and theoretical analysis of matrix-whitening optimizers for deep neural network training, focusing on disentangling the contributions of spectral normalization and variance adaptation. The authors establish a controlled experimental framework to compare a suite of matrix-whitening optimizers, including Shampoo, SOAP, Muon, AdaMuon, SPlus, and PSGD, against elementwise baselines such as Adam and Signum. The paper reveals that while matrix-whitening optimizers consistently outperform elementwise methods, the performance gains are not solely attributable to accurate spectral normalization. Instead, variance adaptation emerges as a critical, and previously underappreciated, component driving optimizer efficacy.
Figure 1: The experimental setup isolates the effects of matrix-whitening optimizers on Transformer training, with hyperparameter sweeps for each method.
Experimental Framework and Benchmarking
The authors employ a rigorous experimental protocol using a GPT-2 "Base" Transformer (162M parameters) trained on OpenWebText for next-token prediction. All optimizer variants are tuned over four key hyperparameters: learning rate, weight decay, , and . Nonstandard parameters (embedding, output, layernorm) are optimized with Adam using fixed hyperparameters to control for confounding factors. Each optimizer is benchmarked for wall-clock time, steps-to-convergence, and final validation loss.
Figure 2: Matrix-whitening optimizers maintain relative performance gains across local hyperparameter adjustments, centered at each method's optimum.
The results demonstrate that matrix-whitening optimizers reach equivalent validation loss in 66–83% of the steps required by Adam, with SOAP and AdaMuon achieving the strongest per-step and wall-clock performance, respectively. These gains persist even under suboptimal hyperparameter settings, indicating robustness to tuning.
Spectral Normalization: Insufficient for Explaining Performance
A central hypothesis in prior work is that matrix-whitening optimizers derive their advantage from more accurate spectral normalization, i.e., descending along the steepest direction under the spectral norm. The paper rigorously tests this by comparing SOAP (explicit eigendecomposition and elementwise normalization in the rotated basis) and Muon (Newton-Schulz iteration for orthogonalization).
Figure 3: Left: Muon achieves tighter singular value spread than SOAP/SPlus, but does not match SOAP's empirical performance. Right: Increasing computation for Muon/SPlus does not close the gap to SOAP.
Empirical analysis shows that Muon achieves a singular value ratio close to 1, outperforming SOAP in spectral normalization accuracy. However, SOAP consistently yields better validation loss, even when its eigenbasis is cached for 100 steps or when only one side is preconditioned. Increasing computational budget for Muon or SPlus does not bridge the performance gap. These findings refute the notion that spectral normalization alone explains the superiority of matrix-whitening optimizers.
Variance Adaptation: The Key Ingredient
The authors identify variance adaptation—elementwise normalization by historical (uncentered) variance—as a decisive factor in optimizer performance. By constructing optimizer pairs that differ only in their use of sign-descent versus variance-adapted descent (e.g., Signum vs. Adam, SPlus vs. SOAP, Muon vs. AdaMuon), they show that variance-adapted variants consistently outperform their sign-descent counterparts, with performance differences comparable to those between Adam and Muon.
Figure 4: Variance-adapted optimizer variants outperform strictly signed-descent counterparts across families; low-rank variance estimators retain performance.
Variance adaptation is shown to be effective regardless of the basis in which it is performed (rotated eigenbasis in SOAP, elementwise in AdaMuon). Theoretical analysis connects variance adaptation to dynamic trust region adjustment proportional to the signal-to-noise ratio, as in adaptive learning rate schemes. The authors further demonstrate that low-rank (rank-1) factorization of the variance buffer, as in Adafactor, reduces memory cost without degrading performance, and sometimes even improves it due to bias-variance tradeoffs.
Ablations: Basis, Parameter Subsets, and Memory Efficiency
The paper includes fine-grained ablations to assess the impact of preconditioning basis and parameter subsets:
- Preconditioning only the input basis in SOAP recovers most of the performance of full SOAP, reducing memory overhead to 41%.
- Applying matrix-whitening only to specific parameter groups (e.g., MLP-In) yields additive performance gains, with the largest benefit observed for highly correlated activations.
Figure 5: SOAP-100 with matrices preconditioned using only one side demonstrates that input-basis preconditioning is nearly as effective as full preconditioning.
Figure 6: Performance gains from SOAP are additive across parameter groups, with MLP-In preconditioning contributing the most.
Trade-offs and Implementation Considerations
The paper provides practical guidance for implementing matrix-whitening optimizers:
- Computational Cost: SOAP and Shampoo require explicit eigendecomposition and matrix power operations, which can be amortized by caching or using low-rank approximations.
- Memory Footprint: Full-matrix variance buffers can be replaced with rank-1 factorizations (Adafactor) for large models.
- Hyperparameter Sensitivity: Matrix-whitening optimizers are robust to local hyperparameter variations but require careful tuning for optimal performance.
- Deployment: For large-scale models, preconditioning only critical parameter groups (e.g., MLP-In) and using low-rank variance adaptation can yield most of the benefits with reduced resource requirements.
Implications and Future Directions
The findings have both practical and theoretical implications:
- Optimizer Design: Matrix-whitening should be viewed as a composition of spectral normalization and variance adaptation, which can be decoupled and recombined for new optimizer variants.
- Theory: The spectral-descent perspective is incomplete; variance adaptation is equally fundamental and should be incorporated into future theoretical analyses.
- Scalability: Efficient implementations (e.g., low-rank variance buffers, selective preconditioning) enable matrix-whitening optimizers to scale to very large models.
- Open Questions: The underlying reason for variance adaptation's effectiveness remains unresolved. Further work is needed to understand its role in deep network generalization and optimization dynamics.
Conclusion
This paper provides a comprehensive deconstruction of matrix-whitening optimizers, demonstrating that both spectral normalization and variance adaptation are essential for strong performance. The empirical evidence refutes the sufficiency of spectral normalization and highlights variance adaptation as a critical, composable ingredient. The work opens new avenues for optimizer design, suggesting that future advances may arise from novel combinations of these components and more efficient implementations. The challenge remains to discover preconditioning schemes that can further double the observed gains, pushing validation loss below current limits.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper studies how to better train large neural networks by improving the “optimizer,” which is the rule that decides how the model’s parameters change during learning. The authors focus on a family of optimizers that use a trick called “matrix whitening.” They ask: what parts of this trick actually make training faster and better?
Key questions
The paper explores three main questions:
- Why do “matrix-whitening” optimizers tend to beat popular methods like Adam?
- Is their advantage mainly because they make all directions of change balanced (“spectral normalization”), or is something else important?
- Can we get the same benefits with simpler, less memory-hungry versions?
How did they test it?
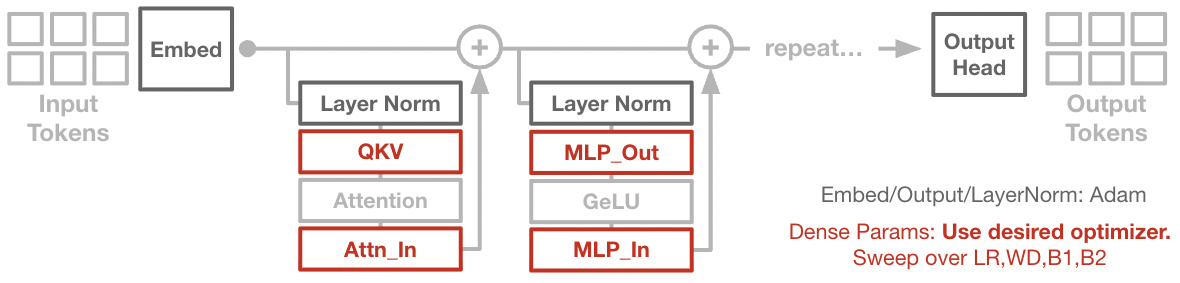
The authors run controlled experiments on a standard LLM (a GPT-2–style Transformer with about 162 million parameters) trained to predict the next word on a real dataset. To make the comparison fair, they:
- Use the same model, data order, random seed, and training setup for each optimizer.
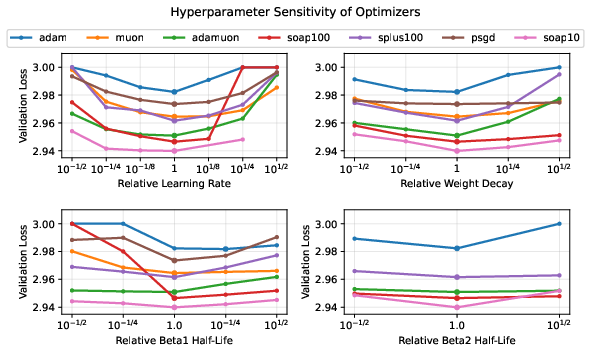
- Tune four key “knobs” (hyperparameters) for every optimizer: learning rate, weight decay, momentum strength (β₁), and variance tracking strength (β₂).
- Strip away extra features so they compare the core behavior of each optimizer.
Everyday analogy:
- Think of training like walking downhill to reach the lowest point (best performance).
- Different optimizers are different kinds of “shoes” and “walking strategies.”
- Matrix whitening is like first stretching and straightening the map so hills tilt evenly, then picking step sizes that match how reliable your direction is.
Terms in simple words:
- Matrix whitening: For weight matrices in a neural network, it adjusts updates so the model doesn’t change too much along directions that are highly linked or “correlated.” It both balances directions and scales steps based on how noisy they are.
- Spectral normalization: Making the “strength” of updates even across directions (like setting all speed limits equal), which helps avoid over-correcting in any one direction.
- Variance adaptation: Shrinking steps when the gradient is noisy and growing steps when it’s stable; similar to trusting calm signals more than jittery ones.
- Adam: A popular optimizer that adapts step sizes per parameter using a simple estimate of variance.
- SOAP, Shampoo, Muon, Signum, AdaMuon: Different ways of doing whitening and/or adapting variance.
Main findings
Here is what they discovered and why it matters:
- Matrix-whitening methods consistently beat Adam when both are properly tuned. That means handling the matrix structure of neural networks really helps.
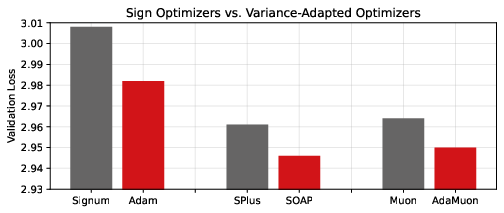
- The optimizer called SOAP gave the biggest improvement per training step, even though Muon was the best at pure spectral normalization. In other words, simply making all directions perfectly balanced was not enough to explain the performance gains.
- The “secret sauce” is variance adaptation. Across three pairs of methods, the versions that adapt to variance (like Adam, SOAP, and AdaMuon) beat their “sign-only” partners (like Signum, SPlus, and Muon). The boost from variance adaptation is large—almost as big as the boost from doing matrix whitening at all.
- “Lookahead” tricks (which try to adjust signs using a peek at the next step) helped a little, but did not replace proper variance adaptation.
- Good news for memory: you can use low-rank variance estimates (a cheaper summary per row and column instead of a full matrix) and still get almost the same performance, sometimes even better. This makes variance adaptation more practical.
Why it matters
- Matrix whitening has two key ingredients: balancing directions (spectral normalization) and adapting to noise (variance adaptation). Both matter, and they can be combined or even done in different stages.
- Methods that only focus on making directions balanced can be improved by adding variance adaptation.
- Saving memory with low-rank variance tracking keeps most of the benefits, making advanced optimizers more accessible.
Potential impact and next steps
This work encourages designing optimizers as mix-and-match components rather than entirely new, separate algorithms. If future methods combine strong spectral normalization with smart variance adaptation—possibly with low memory cost—they could train big models faster and better.
The authors also pose a challenge: can we find a new preconditioning method (a smarter way to scale directions) that doubles these gains and pushes performance even lower under the same budget? Exploring why variance adaptation works so well in deep networks—and how to do it most effectively—looks like a promising path forward.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, actionable list of what remains missing, uncertain, or unexplored in the paper.
- Generality beyond the single setting: Results are limited to GPT‑2 Base on OpenWebText for 10k steps with a specific batch/sequence length; it remains unknown whether the conclusions (especially the primacy of variance adaptation) hold across larger/smaller models, longer trainings, different data ratios, modality changes (vision, speech), and other tasks (e.g., classification, RL, retrieval).
- Long-horizon behavior: The paper focuses on 10k steps; how spectral normalization and variance adaptation influence convergence, stability, and final performance over much longer training (e.g., 100k–1M steps) is untested.
- Hyperparameter coverage gaps: Key knobs like Adam’s ε, warmup length, LR schedules beyond cosine, decoupled vs L2 weight decay, gradient clipping, and momentum variants (e.g., Nesterov) were not explored; their interactions with whitening and variance adaptation could change the conclusions.
- Why SOAP > Muon despite tighter spectral normalization: A concrete mechanistic explanation is missing; design targeted experiments to isolate how SOAP’s rotated elementwise variance adaptation yields superior loss reduction despite Muon’s closer adherence to steepest spectral descent.
- Basis choice for variance adaptation: The paper shows adaptation helps in both rotated (SOAP) and unrotated (AdaMuon) bases, but does not identify when and why one basis is superior; develop criteria or algorithms to select/adapt the variance-adaptation basis per layer and training phase.
- Theoretical reconciliation of trust-region view: Formalize when variance adaptation after orthogonalization (AdaMuon) is equivalent or superior to adaptation in the eigenbasis (SOAP) under the whitening metric; derive conditions under which the signal-to-noise trust-region interpretation predicts performance differences.
- Robustness and failure modes of Shampoo/SOAP: Shampoo-100 “fails to converge” in this setting; the root causes (numerical instability, damping/ε choice, inversion frequency, factor-conditioning) are not identified; perform controlled diagnostics and propose stabilization techniques.
- Dynamic schedules for preconditioner updates: Frequency choices (eigenbasis caching in SOAP, Newton–Schulz iterations in Muon) are static; investigate adaptive schedules (based on curvature change, gradient variance, or compute budget) to optimize wall-clock vs performance trade-offs.
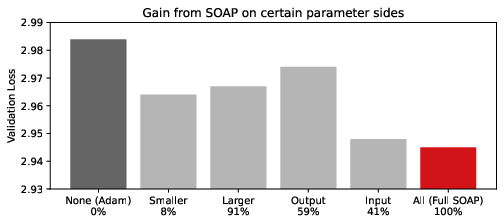
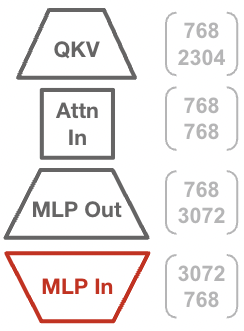
- One-sided vs two-sided preconditioning: Input-side-only preconditioning recovered most SOAP gains in this Transformer; assess whether this asymmetry generalizes across architectures (e.g., attention Q/K/V/O, convolutions, embeddings) and explain the structural reasons (e.g., activation correlation and rank bottlenecks).
- Layerwise contribution and activation correlation: The finding that “MLP In” contributes disproportionately is speculative; quantify input-feature correlation and singular-value structure across layers to predict where whitening helps most, and validate across model sizes and datasets.
- Low-rank variance estimators: Factorized rank‑1 variance often matched (or exceeded, for Muon) full-matrix performance; systematically explore rank selection (rank‑k), dynamic rank, and bias–variance trade-offs to minimize memory without sacrificing accuracy.
- Interaction with weight decay and regularization: Only limited WD sweeps were run; analyze how decoupled weight decay, L2 penalties, dropout, and other regularizers interact with whitening and variance adaptation, including their effects on effective learning rates and curvature.
- Non-matrix parameter treatment: Embeddings, output heads, and layernorm scales were always optimized with Adam; test matrix-whitening or variance adaptation for these subsets (or structured variants), and quantify the net impact and interactions.
- Precision and numerical stability: Optimizer/model precision choices (fp32 optimizer, bf16 activations) may affect spectral operations and variance buffers; paper mixed-precision stability, scaling, and error accumulation across different hardware (GPU/TPU) and kernels.
- Measurement gaps in curvature and noise: The paper uses singular-value ratios of updates but does not measure Hessian/Fisher alignment, curvature spectra over training, or gradient noise scales; add these diagnostics to link optimizer behavior with loss improvements mechanistically.
- Generalization metrics: Only validation loss is reported; evaluate perplexity, out-of-distribution behavior, calibration, and downstream task transfer to ensure whitening/variance adaptation improvements are not narrowly overfitting the benchmark.
- Lookahead alternatives: “Lookahead” sign methods underperform but were explored narrowly; investigate richer memory-efficient second-moment approximations (e.g., sketching, diagonal‑plus‑low‑rank, blockwise statistics) and adaptive β3 schemes before dismissing lookahead as a viable substitute.
- Scheduling β1 and β2: The paper notes benefits of variance adaptation but does not explore time-varying β1/β2 (e.g., annealing, layerwise β’s, coupling to batch size/noise scale); test whether dynamic schedules yield further gains or reduce sensitivity.
- Cross-layer or cross-parameter whitening: Current methods whiten per-layer matrices independently; evaluate whether coupling across layers (e.g., block-diagonal or cross-layer Kronecker structures) yields larger gains or harms stability.
- Gradient clipping and safety: Interactions between whitening, variance adaptation, and clipping (norm or adaptive) were not studied; assess whether clipping helps control rare spikes in spectral operations or undermines variance-adapted trust regions.
- Adaptive basis selection and partial updates: The paper suggests output-side preconditioning can be skipped; explore algorithms that learn which side(s) or subspaces to precondition and when, possibly guided by activation/gradient statistics.
- Compute–accuracy frontier: Wall-time comparisons are informative but hardware-dependent; build a standardized cost model (FLOPs, memory traffic, kernel fusion) for each optimizer to guide deployment under different accelerator constraints.
- Extending to alternative architectures: Test conclusions in models with different parameter structures (e.g., CNNs, state-space models, mixture-of-experts), where Kronecker factors and spectral properties differ; identify domains where whitening is most beneficial.
- Formal link to natural gradient and Fisher: The whitening metric is related to Fisher/Hessian approximations, but the paper does not quantify proximity; measure and exploit this link to design more principled preconditioners that combine spectral normalization with variance adaptation.
- The “< 2.90” challenge: The paper sets an open performance target but offers no concrete pathways; propose and test candidate directions (e.g., cross-layer whitening, curvature‑aware trust-region schedules, hybrid Fisher–Kronecker preconditioning, adaptive rank variance) to systematically pursue the targeted improvement.
Practical Applications
Immediate Applications
The paper’s findings and ablations translate into several actionable improvements for model training workflows today. The core takeaways to deploy now are: (1) replace elementwise optimizers (e.g., Adam) with matrix-whitening variants, (2) ensure variance adaptation is present (not just signed descent), and (3) use low-rank/frequency/basis approximations to control compute and memory.
- Sector: Software/AI Infrastructure, Cloud/ML Platforms
- Optimizer upgrades in training stacks
- Replace Adam with:
- SOAP-100 for best per-step progress with modest wall-clock overhead (≈1.2× per-step cost vs Adam; ≈11–15% faster time-to-target loss vs Adam due to needing only ~71–74% of Adam’s steps).
- AdaMuon for the best speed/quality trade-off (≈1.07× per-step cost; ≈18–21% faster time-to-target loss).
- When time-to-target matters, prefer AdaMuon or SOAP-100; avoid SOAP-10 unless step budgets (not wall-clock) are the primary constraint.
- Assumptions/dependencies: benefits measured on a 162M GPT-2 model; results likely but not guaranteed to transfer—verify with a brief sweep on your models/tasks/hardware.
- Low-memory variance adaptation drop-in
- Use rank-1 (Adafactor-style) variance buffers with matrix-whitening optimizers to reduce memory from O(mn) to O(m+n) with negligible (often zero) loss degradation; sometimes improves stability and performance.
- Assumptions/dependencies: factorized estimators work well in tested transformer blocks; confirm on convs/attention variants.
- Basis/side selection for preconditioning
- Precondition only the input side (one-sided SOAP/Shampoo) to recover most of the gains at ~41% of the memory cost of full two-sided whitening.
- Assumptions/dependencies: asymmetry depends on architecture; input-side advantage observed on GPT-2-base.
- Practical hyperparameter sweeps
- Adopt the paper’s four-parameter sweep template (LR, weight decay, β1, β2) with coarse logarithmic resolutions to reach near-optimal settings quickly.
- Tools/workflow: add a routine in AutoML/Bayesian tuning pipelines that locks non-matrix params to Adam while sweeping matrix-whitening hyperparameters; store “known good” defaults for each optimizer flavor to minimize tuning burden.
- Assumptions/dependencies: the reported step-size resolutions (e.g., 101/8 LR) are sufficient to resolve optimizer gaps in similar regimes; adapt if your loss landscape is sharper/flatter.
- Training observability
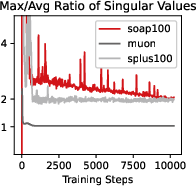
- Monitor the “spectral max/mean” ratio of update singular values and the variance buffers; trigger dynamic reconfiguration (e.g., shorten eigenbasis cache interval or switch to input-only preconditioning) if ratios drift.
- Tools: add optimizer telemetry panels (spectral spread, EMA variances) to MLFlow/W&B dashboards.
- Sector: LLM Fine-Tuning/Instruction Tuning, RL/Robotics, Multimodal
- Budget-limited training
- Use AdaMuon or SOAP-100 to improve final quality within fixed step budgets (consistent ~0.02–0.04 validation loss improvements over Adam in the tested setup).
- For high-variance gradients (common in RL and small-batch fine-tuning), enable variance adaptation explicitly (avoid pure signed-descent like Signum/SPlus).
- Assumptions/dependencies: step-to-quality gain extrapolates to low-data/finetuning settings; verify on-task.
- Parameter-subset targeting
- If you cannot switch the entire model to matrix-whitening, prioritize MLP input matrices (where gains are largest) to capture a disproportionate share of the benefit.
- Workflow: conditional optimizer routing—route MLP-In params to SOAP-100 or AdaMuon; keep others on Adam/Adafactor.
- Assumptions/dependencies: the predominance of MLP-In benefits may vary across architectures and widths.
- Edge and on-device fine-tuning
- Use low-rank variance adapters + one-sided preconditioning to fit memory constraints while retaining most gains.
- Tools/products: mobile-friendly AdaMuon-FA (factorized variance) variants for LoRA/adapter-based fine-tuning.
- Sector: Energy/Green AI, Finance (Cost Optimization), Ops
- Cost and carbon reduction
- Expect fewer steps to reach a target loss (≈66–83% of Adam’s steps in the reported setup); choose variants (AdaMuon/SOAP-100) that also improve wall-clock to cut compute cost and CO2.
- Workflow: cost-aware optimizer selection—benchmark AdaMuon vs Adam for your largest spend training jobs; adopt where time-to-target shows ≥10% improvement.
- Assumptions/dependencies: speedups are hardware/implementation dependent; measure on your stack (BLAS kernels, GPU gen, distributed communication).
- Sector: Academia/Research
- Component-based optimizer research methodology
- Use the paper’s decomposition to test interchangeable components: spectral normalization method (NS vs eigensolvers), variance adaptation (full vs factorized), basis choice (one- vs two-sided), update frequency (N=10 vs 100).
- Tools: reuse the provided GitHub code to build standardized, component-level ablations in new domains (vision, speech, RL).
- Teaching and reproducibility
- Adopt the paper’s controlled comparison design (shared seeds, same non-matrix optimizer, identical data order) in coursework and publications to reduce confounders.
- Policy for labs/venues: require disclosure of per-optimizer hyperparameter sweeps and non-matrix parameter handling.
- Sector: MLOps/Tooling Vendors
- Productize “Optimizer-as-a-Feature”
- Add SOAP-100/AdaMuon presets with automatic memory-saving modes (factorized variance, input-only) and scheduler knobs (eigenbasis refresh interval).
- Provide “adaptive mode” that toggles between signed/variance-adapted updates when noise estimates justify it.
- Assumptions/dependencies: stable kernel performance for repeated eigendecompositions; robust numerical handling in bf16/fp16.
- Sector: Daily Life (indirect)
- Better AI-powered apps through faster/better training
- Shorter iteration loops in companies mean faster feature delivery and improved model quality for translation, recommendations, and personalization.
- On-device personalization benefits from low-memory variance-adapted optimizers (longer battery, less heat during brief training bursts).
- Assumptions/dependencies: depends on downstream adoption in model providers and mobile frameworks.
Long-Term Applications
These opportunities build on the paper’s insight that whitening has two separable roles—spectral normalization and variance adaptation—and that low-rank techniques can preserve performance. They require further scaling, validation beyond the tested regime, and deeper systems integration.
- Sector: Software/AI Infrastructure, Hardware Co-Design
- Optimizer-aware compiler/runtime integration
- Fuse eigendecompositions/Newton–Schulz steps with gradient pipelines (e.g., CUDA Graphs, Triton kernels) to bring SOAP-10’s per-step gains without the wall-clock penalty.
- Hardware features (tensor-core modes) specialized for frequent small/medium eigen/singular-factor updates.
- Dependencies: kernel engineering, vendor support; validation on very large models (billions of params).
- Dynamic optimizer switching
- Train-time controllers that switch between signed, variance-adapted, and fully whitened modes based on measured signal-to-noise, curvature proxies, or spectral spread.
- Potential tools: RL-based or bandit schedulers for optimizer state transitions.
- Dependencies: robust online metrics; low-latency control loops; guardrails to prevent instability.
- Sector: Foundation Models, Safety/Alignment
- Trust-region and noise-aware training policies
- Embed variance-adapted learning-rate modulation as an explicit, auditable trust-region constraint across large-scale training runs to reduce catastrophic spikes and improve stability.
- Dependencies: standards for logging noise estimates; integration with safety monitors and early-stopping logic.
- Sector: Robotics/Autonomy, RL at Scale
- High-variance regime optimizers
- Optimizers tuned for stochastic, nonstationary gradients (RL, sim2real), combining orthogonalization with factorized variance adaptation and schedule-aware β1/β2.
- Products: “AdaMuon-RL” with entropy/advantage-aware noise estimates; curricula that modulate variance adaptation strength over training phases.
- Dependencies: empirical validation in on-policy/off-policy pipelines; interplay with target networks and critic-stability tricks.
- Sector: Healthcare, Finance, Scientific ML
- Efficient training under data and compute constraints
- Domain-tuned whitening strategies for tabular transformers, time-series models, and graph nets where correlated features are prominent; one-sided preconditioning aligned with domain-specific layer asymmetries.
- Products/workflows: “input-basis-first” recipes for EHR time-series transformers; low-rank variance adaptation defaults for privacy-preserving/federated settings.
- Dependencies: regulatory validation; robustness under distribution shift.
- Sector: Education, Open Science, Standards
- Benchmarking standards for optimizer comparisons
- Community frameworks that enshrine component-level ablations, uniform seeds/data order, and multi-resolution hyperparameter sweeps, preventing misleading optimizer claims.
- Policies: venues and consortia recommend reporting spectral spread and variance metrics, and require tuning parity across methods.
- Dependencies: agreement among benchmark maintainers; compute sponsorship for fair sweeps.
- Sector: Energy/Green AI, Policy
- Compute-efficiency incentives
- Grant and procurement guidelines that score proposals based on demonstrated optimizer efficiency (step-to-target and wall-clock-to-target), not just final quality.
- Carbon accounting that attributes savings to optimizer choice and publishes “optimizer efficiency reports” with models.
- Dependencies: standardized measurement protocols; buy-in from funding bodies and cloud providers.
- Sector: New Optimizer Families
- Decoupled designs beyond whitening
- Novel preconditioners that separately target correlation structure (spectral/orthogonalization) and noise structure (variance/trust-region) with different bases and ranks, potentially surpassing current gains.
- Tools/products: libraries offering “optimizer composers” letting users choose basis (identity/eigen/NS), variance rank (full/factorized), update cadence, and side(s).
- Dependencies: theory to guide basis selection; large-scale empirical validation.
- Sector: Edge/Federated ML
- Communication- and memory-efficient training
- Factorized variance adaptation paired with infrequent, one-sided whitening to fit mobile and federated constraints while maintaining training quality.
- Products: federated SDKs with AdaMuon-FA and adaptive preconditioner refresh schedules to minimize uplink/downlink.
- Dependencies: secure aggregation compatible with optimizer state; resilience to heterogeneous client hardware.
Notes on assumptions and transferability
- The strongest evidence comes from a 162M-parameter GPT-2 trained on OpenWebText for 10k steps. While whitening plus variance adaptation is broadly motivated, expect to retune LR/WD/β1/β2 and eigenbasis refresh cadences for:
- Very large models, different batch sizes, alternate modalities (vision/audio/graphs), and non-language objectives.
- Different numeric precisions (bf16/fp16), kernel libraries, and distributed settings (data/pipeline/tensor parallel).
- Wall-clock benefits depend on your hardware and eigendecomposition/Newton–Schulz implementations; measure per-step overhead and step-reduction jointly.
- Low-rank variance estimators and one-sided whitening are robust in this paper; verify layerwise on your architecture, especially for atypical shapes (depthwise convs, MoEs).
Glossary
- AdaMuon: A Muon variant that applies elementwise variance normalization to post-orthogonalized updates. "AdaMuon \citep{si2025adamuon}, a variant on Muon where a variance buffer is estimated over post-orthogonalized updates, and is used for elementwise normalization."
- Adafactor: An optimizer that uses low-rank (factorized) second-moment estimates to reduce memory. "We utilize the following scaled Adafactor \citep{shazeer2018adafactor} update:"
- Adam: A widely used optimizer combining momentum with elementwise adaptive preconditioning via second moments. "Adam \citep{kingma2014adam}, a baseline optimizer that is the current standard for training deep neural networks."
- Chinchilla ratio: A compute-optimal training ratio relating model size and dataset size. "which is roughly a 1x Chinchilla ratio \citep{hoffmann2022training}."
- cosine learning rate schedule: A learning-rate decay scheme that follows a cosine curve. "We use a fixed warmup of 200 steps and a cosine learning rate schedule afterwards."
- Dion: An orthogonalization-focused optimizer proposed as an alternative to Muon-like methods. "pure orthogonalization methods -- such as Muon, Dion \citep{ahn2025dion} and Polargrad \citep{lau2025polargrad}, among others -- can be further improved."
- eigenbasis: The basis formed by a matrix’s eigenvectors used to rotate and normalize updates. "SOAP \citep{vyas2024soap}, a variant of Shampoo where updates are rotated onto the eigenbasis of the left/right factors."
- eigendecomposition: The factorization of a matrix into its eigenvectors and eigenvalues. "the explicit eigendecomposition used in Shampoo-style methods."
- exponential moving average (EMA): A recursive average that weights recent observations more heavily. "i.e. an exponential moving average of the centered variance of gradients."
- Fisher information matrix: A matrix capturing the curvature of the loss landscape in parameter space under probabilistic models. "to natural gradient descent over a form of the Fisher information matrix \citep{amari1998natural, sohl2012natural, kunstner2019limitations}"
- Gauss-Newton approximation: A positive semi-definite approximation to the Hessian used in second-order optimization. "related to second-order descent over the Hessian (in particular, the Gauss-Newton approximation) \citep{martens2010deep, korbit2024exact, bottou2018optimization, schraudolph2002fast, li2017preconditioned, pooladzandi2024curvature, lecun2002efficient, liu2023sophia}"
- GELU activation: A smooth nonlinearity commonly used in Transformers. "a 3072-dimensional vector modulated by the
geluactivation" - K-FAC: An optimizer that uses Kronecker-factored approximations to curvature matrices. "K-FAC \citep{martens2015optimizing} introduced a dimension-wise Kronecker factorization scheme, which was further refined in Shampoo \citep{gupta2018shampoo} and its variants."
- Kronecker approximation: Approximating a large covariance/moment matrix with the Kronecker product of smaller factors. "The key benefit of Kronecker approximation is that we can precondition via the inverted Kronecker factors directly, without ever actually forming the full product."
- Kronecker factors: The small matrices whose Kronecker product approximates a larger structured matrix. "we can represent the per-layer whitening metric in terms of its Kronecker factors."
- Kronecker factorization: Decomposing a large structured matrix into a Kronecker product of smaller matrices. "introduced a dimension-wise Kronecker factorization scheme"
- Kron variety: A PSGD variant that applies Kronecker-factorized curvature approximations. "PSGD \citep{li2017preconditioned, li2018preconditioner} also utilizes this scheme in its Kron variety."
- Lion: A lookahead-style signed optimizer that reduces memory by eschewing second moments. "Signed methods employing \"lookahead\" techniques (e.g. Lion \cite{chen2023symbolic} and under loose interpretations MARS \cite{yuan2024mars} or Cautious optimizers \citep{liang2024cautious})"
- lookahead: A technique that forms an update using a convex combination of momentum and current gradient to stabilize signs. "Signed methods employing \"lookahead\" techniques (e.g. Lion \cite{chen2023symbolic}...)"
- Matrix-whitening: A family of methods that normalize gradients using matrix-based second-moment structure. "A range of recent optimizers have emerged that approximate the same matrix-whitening transformation in various ways."
- Muon: An optimizer that orthogonalizes updates via Newton–Schulz iteration to enforce unit singular values. "Muon \citep{jordanmuon}, which orthogonalizes updates via Newton-Shulz iteration, and can be seen as descending under the spectral norm"
- natural gradient descent: Optimization that rescales gradients by an information-geometric metric (often Fisher). "to natural gradient descent over a form of the Fisher information matrix \citep{amari1998natural, sohl2012natural, kunstner2019limitations}"
- Newton-Schulz iteration: An iterative method to compute matrix inverses or square roots used for orthogonalization. "Newton-Schulz iteration to implicitly orthogonalize the momentum buffer"
- non-Euclidean metric: A parameter-space distance measure defined by a positive-definite matrix rather than the standard Euclidean norm. "Gradient descent on non-Euclidean metrics."
- orthogonalization: Transforming a matrix (or update) to have orthonormal singular vectors and unit singular values. "the term above is equivalent to the orthogonalization of "
- Polargrad: An orthogonalization-based optimizer proposed as an alternative to Muon-like methods. "pure orthogonalization methods -- such as Muon, Dion \citep{ahn2025dion} and Polargrad \citep{lau2025polargrad}, among others -- can be further improved."
- preconditioner: A matrix (often an inverse curvature or moment estimate) used to transform gradients before the parameter update. "where and is sometimes referred to as a preconditioner."
- PSGD: A preconditioned SGD method that learns Kronecker-factored preconditioners iteratively. "PSGD (Fisher-Kron) \citep{li2017preconditioned, li2018preconditioner}, which keeps track of a left/right preconditioner that is learned via iterative gradient descent."
- rank-1 approximation: An approximation of a matrix by the outer product of two vectors to reduce memory and computation. "utilize a rank-1 approximation of the variance buffer, reducing memory usage from to ."
- Shampoo: A matrix optimizer that maintains Kronecker-factored second moments and applies matrix powers for whitening. "Shampoo \citep{gupta2018shampoo, shi2023distributed}, a matrix optimizer which explicitly tracks Kronecker factors as in \cref{eq:kronecker}."
- Signum: A signed-gradient optimizer that updates using only the sign of the momentum/gradient. "Signum \citep{bernstein2018signsgd}, which updates via the elementwise sign rather than normalizing by second-moment."
- SPlus: A signed variant of SOAP that rotates into the eigenbasis but uses elementwise sign instead of second moments. "SPlus \citep{frans2025stable}, which similarly to SOAP rotates updates onto the eigenbasis, but takes the elementwise sign rather than normalizing by an explicit second moment buffer."
- SOAP: A Shampoo-style optimizer that rotates into the eigenbasis and applies elementwise variance normalization before rotating back. "SOAP \citep{vyas2024soap}, a variant of Shampoo where updates are rotated onto the eigenbasis of the left/right factors."
- spectral descent: Optimization that follows the steepest descent direction under a spectral norm geometry. "its interpretation as steepest spectral descent \citep{bernstein2024old}"
- spectral norm: The largest singular value of a matrix, measuring its operator norm. "the solution to steepest descent under the spectral norm of the matrix."
- spectral normalization: Rescaling updates so singular values are controlled (often driven toward unity). "performance gains are not explained solely by accurate spectral normalization"
- singular-value decomposition (SVD): Factorization of a matrix into orthogonal matrices and singular values. "singular-value decomposition, "
- signal-to-noise trust region: A perspective that bounds step sizes based on gradient signal-to-noise. "to a signal-to-noise trust region \citep{balles2018dissecting, orvieto2025search}"
- uncentered variance: A second moment estimate without subtracting the mean, used for elementwise normalization. "normalized via an elementwise uncentered variance (i.e. an inner Adam update), then rotated back."
- variance adaptation: Elementwise scaling of updates by estimated variance to modulate step sizes. "the variance adaptation component of matrix-whitening is the overlooked ingredient explaining this performance gap."
- whitening metric: A metric that rescales gradients by the square root of their covariance to decorrelate and normalize. "which we refer to as the whitening metric following \citep{yang2008principal}."
Collections
Sign up for free to add this paper to one or more collections.