Fantastic Pretraining Optimizers and Where to Find Them (2509.02046v1)

Abstract: AdamW has long been the dominant optimizer in LLM pretraining, despite numerous claims that alternative optimizers offer 1.4 to 2x speedup. We posit that two methodological shortcomings have obscured fair comparisons and hindered practical adoption: (i) unequal hyperparameter tuning and (ii) limited or misleading evaluation setups. To address these two issues, we conduct a systematic study of ten deep learning optimizers across four model scales (0.1B-1.2B parameters) and data-to-model ratios (1-8x the Chinchilla optimum). We find that fair and informative comparisons require rigorous hyperparameter tuning and evaluations across a range of model scales and data-to-model ratios, performed at the end of training. First, optimal hyperparameters for one optimizer may be suboptimal for another, making blind hyperparameter transfer unfair. Second, the actual speedup of many proposed optimizers over well-tuned baselines is lower than claimed and decreases with model size to only 1.1x for 1.2B parameter models. Thirdly, comparing intermediate checkpoints before reaching the target training budgets can be misleading, as rankings between two optimizers can flip during training due to learning rate decay. Through our thorough investigation, we find that all the fastest optimizers such as Muon and Soap, use matrices as preconditioners -- multiplying gradients with matrices rather than entry-wise scalars. However, the speedup of matrix-based optimizers is inversely proportional to model scale, decreasing from 1.4x over AdamW for 0.1B parameter models to merely 1.1x for 1.2B parameter models.

• The paper shows that rigorous hyperparameter tuning reduces alternative optimizer speedup claims to a maximum of 1.4× for small models.
• Matrix-based optimizers outperform scalar methods at low data-to-model ratios, but their advantage decreases with increased model scale and data budgets.
• Early-stage evaluations can mislead; only final checkpoint comparisons accurately reflect optimizer performance differences.

Systematic Benchmarking of Pretraining Optimizers: Insights and Implications

Introduction

The paper "Fantastic Pretraining Optimizers and Where to Find Them" (2509.02046) presents a comprehensive empirical paper of optimizer performance in LLM pretraining. The authors address two pervasive methodological flaws in prior optimizer research: insufficient hyperparameter tuning and limited evaluation regimes. By rigorously benchmarking eleven optimizers—including both scalar- and matrix-based methods—across multiple model scales and data-to-model ratios, the paper provides a robust assessment of optimizer efficacy, scaling behavior, and practical speedup claims.

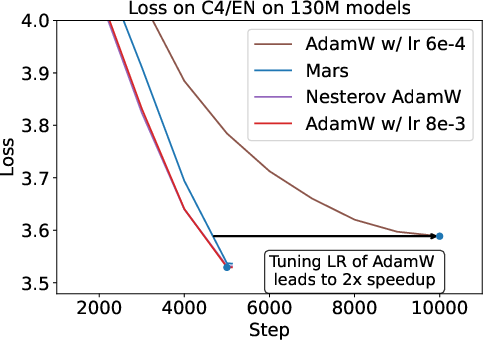
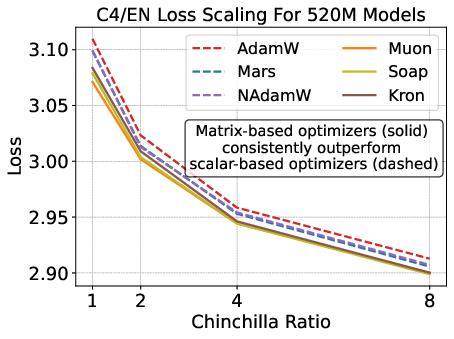
Figure 1: The commonly used AdamW baseline for optimizer design is under-tuned; proper hyperparameter optimization can yield up to 2× speedup for small models.

Experimental Design and Methodology

The paper employs a three-phase hyperparameter tuning protocol:

• Phase I: Exhaustive coordinate descent sweeps for each optimizer across six regimes (three model sizes, four data-to-model ratios), identifying scaling-sensitive hyperparameters.
• Phase II: Focused sweeps on scaling-sensitive hyperparameters, enabling efficient extrapolation to larger models and higher data budgets.
• Phase III: Fitting scaling laws to predict optimal hyperparameters for 1.2B parameter models and beyond.

All experiments use the Llama 2 architecture (0.1B–1.2B parameters) and a large-scale, diverse pretraining corpus. The primary evaluation metric is final validation loss on C4/EN, with downstream performance tracked on a suite of standard benchmarks.

Main Empirical Findings

1. Hyperparameter Tuning is Critical

The paper demonstrates that prior claims of 1.4–2× speedup for alternative optimizers are largely artifacts of under-tuned AdamW baselines. Rigorous sweeps reveal that the true speedup over a well-tuned AdamW is at most 1.4× for small models, diminishing to 1.1× for 1.2B parameter models.

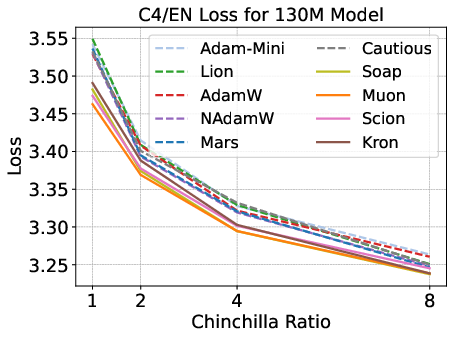
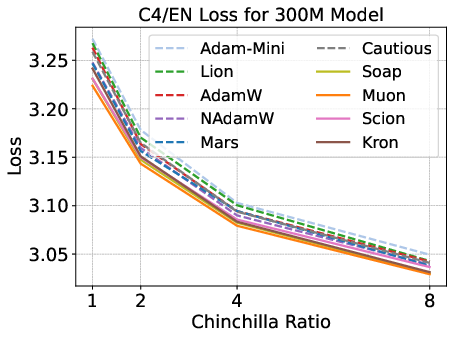
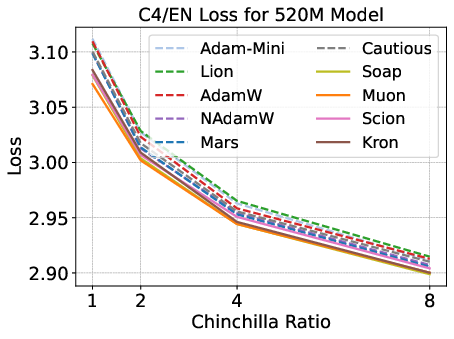
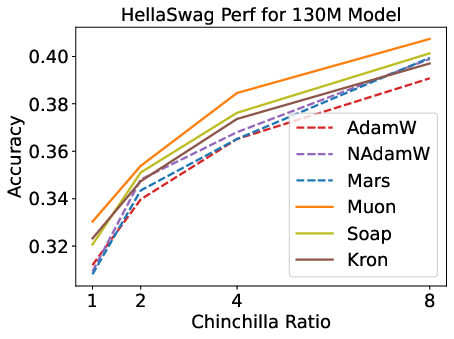
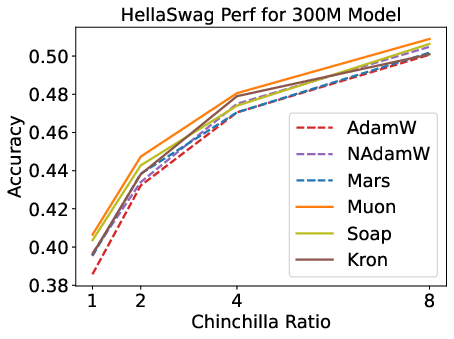
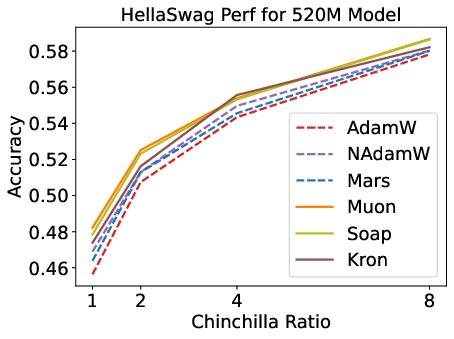
Figure 2: Validation loss and HellaSwag performance for optimizers across model scales and Chinchilla ratios; matrix-based optimizers outperform scalar-based methods, but speedup is modest.

2. Matrix-Based Optimizers: Scaling and Regime Dependence

Matrix-based optimizers (e.g., Muon, Soap, Kron) consistently outperform scalar-based methods (AdamW, Lion, Mars) for small models and low data-to-model ratios. However, their advantage diminishes with increasing model size and data budget. Notably, Muon is optimal at 1–4× Chinchilla ratios, but Soap and Kron surpass Muon at higher ratios (≥8×).

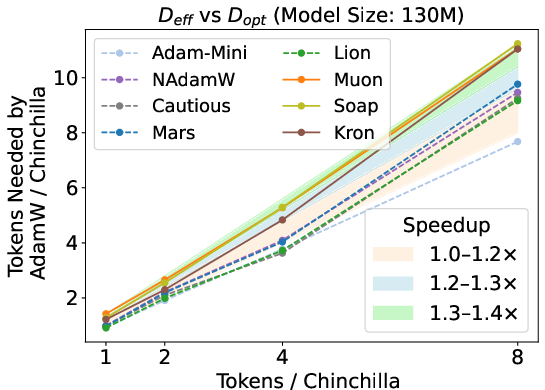
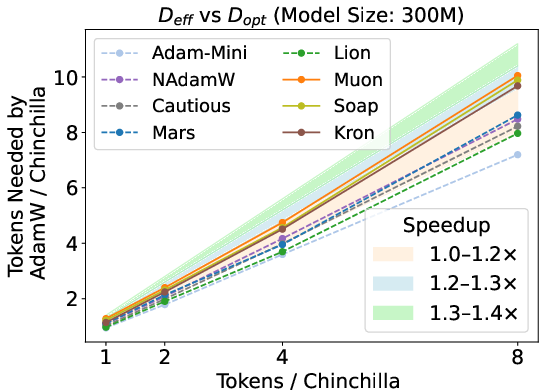
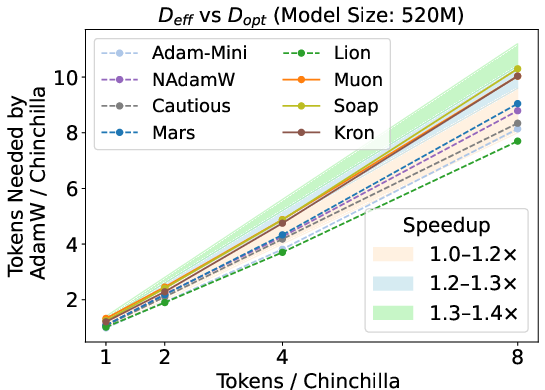
Figure 3: Estimated speedup of optimizers by mapping loss to equivalent data budget; matrix-based methods show increasing speedup with data budget, but the highest speedup is capped at 1.4×.

3. Early-Stage Evaluation is Misleading

Optimizer rankings can flip during training due to learning rate decay and other schedule effects. Intermediate checkpoint comparisons are unreliable; only end-of-training evaluations yield valid conclusions.

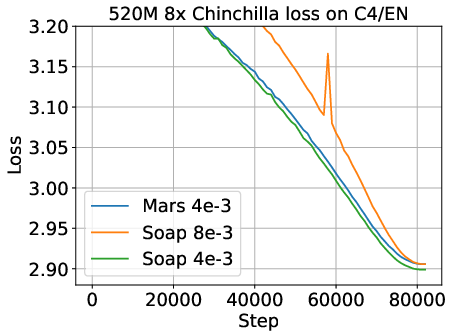
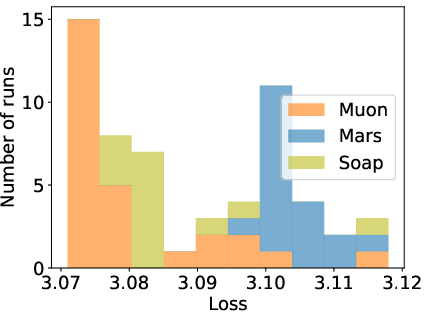
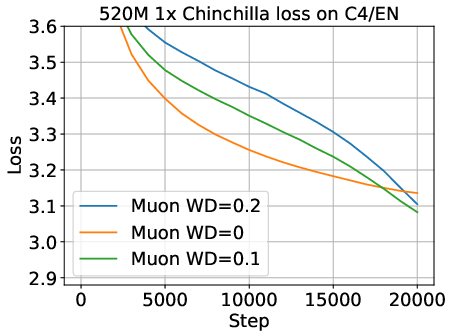
Figure 4: Hyperparameter sensitivity and early-stage loss curves; suboptimal tuning or premature evaluation can arbitrarily flip optimizer rankings.

4. Common Optimization Phenomena

Across all optimizers, parameter norms track learning rate schedules, and gradient norms increase during learning rate decay without corresponding loss increases. Generalization behavior is similar for all optimizers at the tested scales.

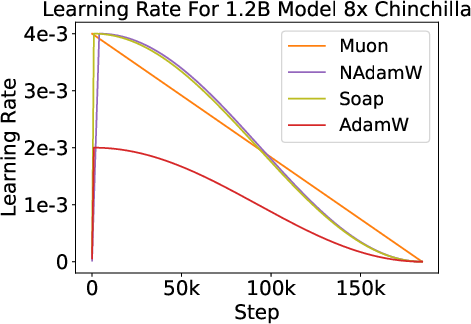
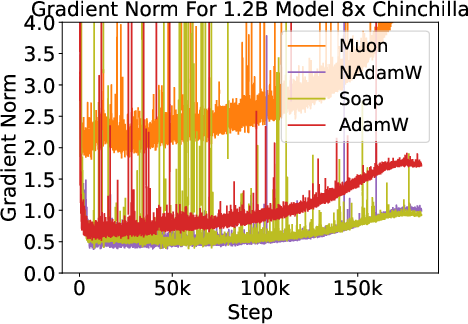
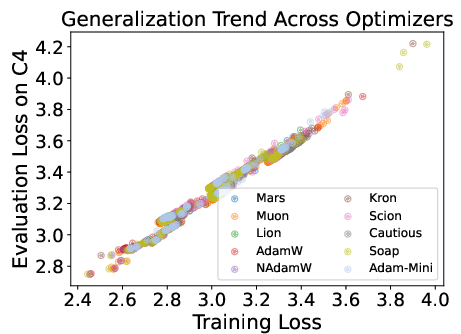
Figure 5: Shared phenomena across optimizers—parameter and gradient norm evolution, and similar generalization trends.

Case Studies and Scaling Law Extrapolation

Scaling laws fitted from the empirical data predict that matrix-based optimizers' speedup vanishes at larger scales (e.g., 7B parameters), with Muon potentially underperforming AdamW in the 1× Chinchilla regime. In high data-to-model ratio settings (16× Chinchilla), Soap outperforms Muon, indicating that second-order momentum and adaptivity to parameter heterogeneity become increasingly important.

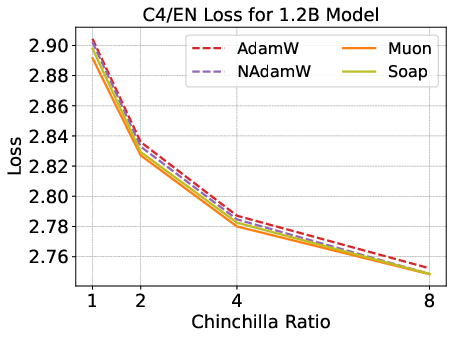
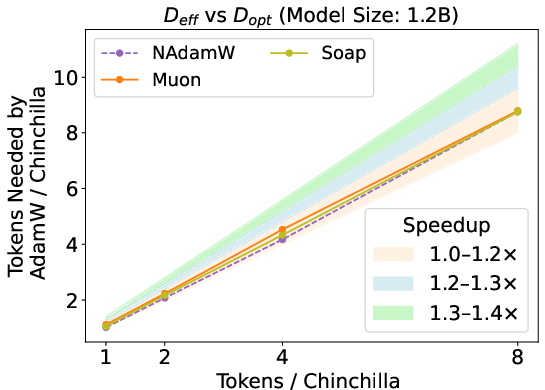
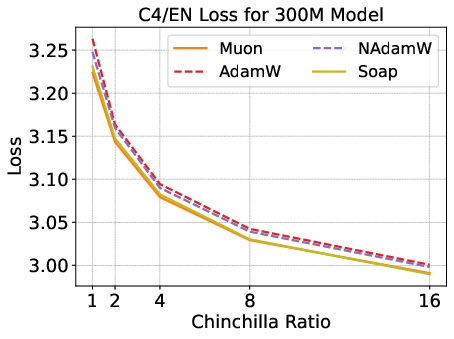
Figure 6: Validation loss scaling and speedup ratios for 1.2B models; matrix-based optimizers' speedup decays to 1.1×, with no significant downstream improvements.

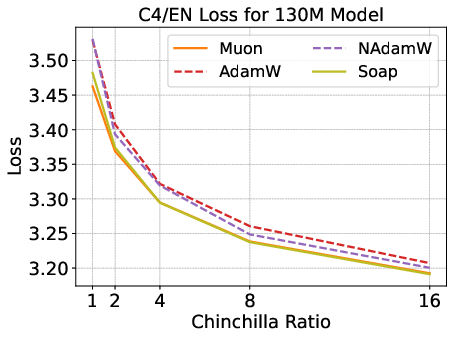
Figure 7: In the 130M 16× Chinchilla regime, SOAP outperforms Muon in overtraining settings.

Implementation Considerations

• Hyperparameter Transfer: Optimal hyperparameters are optimizer-specific; blind transfer leads to unfair comparisons.
• Computational Overhead: Matrix-based optimizers can be implemented with <10% step-wise overhead using blocking and efficient matrix operations.
• Evaluation Protocol: Only final checkpoints should be used for optimizer comparison; intermediate losses are unreliable.
• Scaling Law Fitting: Nonlinear least-squares fitting of hyperparameter scaling laws enables extrapolation to larger models and data budgets.

Implications and Future Directions

The paper refutes strong speedup claims for alternative optimizers in LLM pretraining, showing that rigorous benchmarking yields modest improvements over AdamW. The diminishing returns with scale suggest that optimizer design must account for scaling laws to remain effective at frontier model sizes. Future research should extend benchmarking to models beyond 1.2B parameters and explore optimizers with scale-invariant efficiency.

Conclusion

This work establishes that optimizer benchmarking in LLM pretraining requires exhaustive hyperparameter tuning and principled evaluation protocols. Matrix-based optimizers offer consistent but modest speedups over AdamW for small models and low data-to-model ratios, but their advantage diminishes with scale. The findings underscore the necessity of rigorous methodology in optimizer research and highlight open challenges in designing optimizers that maintain efficiency under scaling laws.