Ax-Prover: A Deep Reasoning Agentic Framework for Theorem Proving in Mathematics and Quantum Physics (2510.12787v2)

Abstract: We present Ax-Prover, a multi-agent system for automated theorem proving in Lean that can solve problems across diverse scientific domains and operate either autonomously or collaboratively with human experts. To achieve this, Ax-Prover approaches scientific problem solving through formal proof generation, a process that demands both creative reasoning and strict syntactic rigor. Ax-Prover meets this challenge by equipping LLMs, which provide knowledge and reasoning, with Lean tools via the Model Context Protocol (MCP), which ensure formal correctness. To evaluate its performance as an autonomous prover, we benchmark our approach against frontier LLMs and specialized prover models on two public math benchmarks and on two Lean benchmarks we introduce in the fields of abstract algebra and quantum theory. On public datasets, Ax-Prover is competitive with state-of-the-art provers, while it largely outperforms them on the new benchmarks. This shows that, unlike specialized systems that struggle to generalize, our tool-based agentic theorem prover approach offers a generalizable methodology for formal verification across diverse scientific domains. Furthermore, we demonstrate Ax-Prover's assistant capabilities in a practical use case, showing how it enabled an expert mathematician to formalize the proof of a complex cryptography theorem.

• The paper demonstrates that Ax-Prover integrates a multi-agent workflow leveraging Lean tools via MCP to achieve robust automated theorem proving.
• It employs specialized agents—Orchestrator, Prover, and Verifier—that work collaboratively to iteratively synthesize and verify proofs in both mathematics and quantum theory.
• Experimental results highlight significant performance gains on math and quantum benchmarks, underscoring Ax-Prover’s efficiency, generalization, and practical applicability.

Ax-Prover: Agentic Theorem Proving Across Mathematics and Quantum Physics

Introduction

The paper introduces Ax-Prover, a multi-agent system for automated theorem proving in Lean, designed to operate both autonomously and collaboratively with human experts. Ax-Prover leverages general-purpose LLMs, equipped with Lean tools via the Model Context Protocol (MCP), to address the limitations of specialized provers—namely, poor generalization, brittleness to library changes, and high deployment costs. The system is evaluated on established mathematics benchmarks and two new datasets in abstract algebra and quantum theory, demonstrating strong performance and domain generalization.

System Architecture

Ax-Prover is structured as a multi-agent workflow comprising three specialized agents: Orchestrator, Prover, and Verifier. Each agent is instantiated as an LLM with tailored prompts and responsibilities. The Orchestrator manages task assignment and feedback routing, the Prover constructs proofs via iterative reasoning and tool calls, and the Verifier certifies correctness using Lean diagnostics.

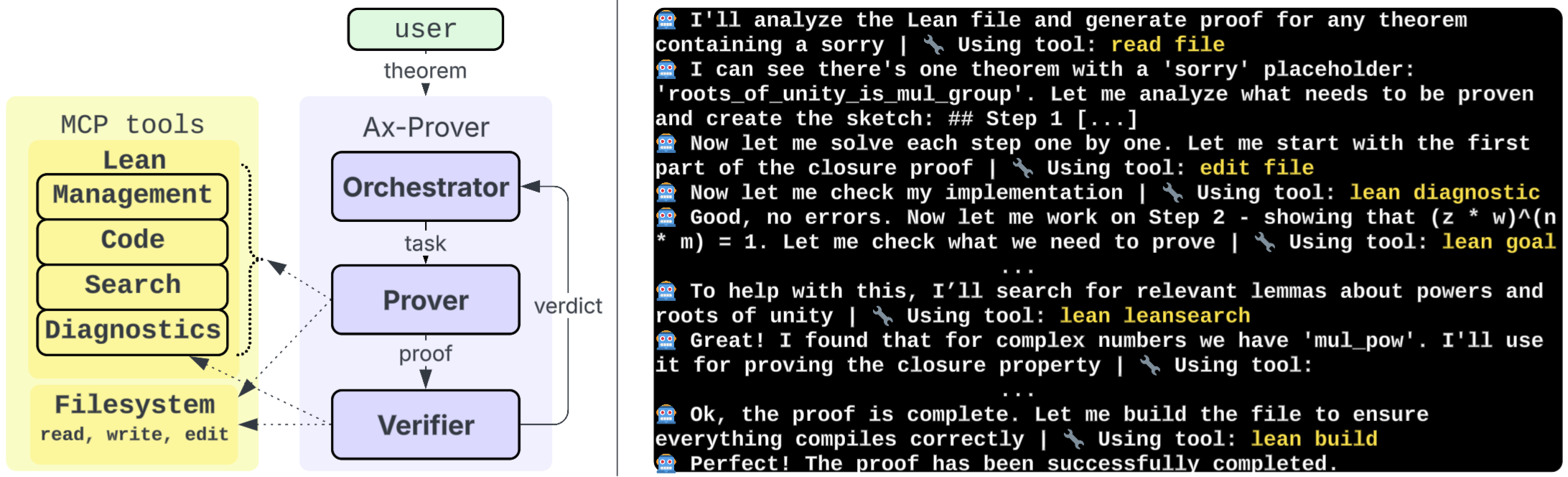
Figure 1: Left: the multi-agent workflow of Ax-Prover. Right: the tool-enhanced reasoning of the Prover.

The Prover agent employs an incremental, stepwise approach to proof synthesis. It identifies unfinished theorems, generates proof sketches, formalizes intermediate steps, and iteratively applies Lean tactics, leveraging MCP tools for goal inspection, theorem search, and error diagnosis. The Verifier independently compiles and checks the proof, ensuring robustness against premature termination or incomplete reasoning.

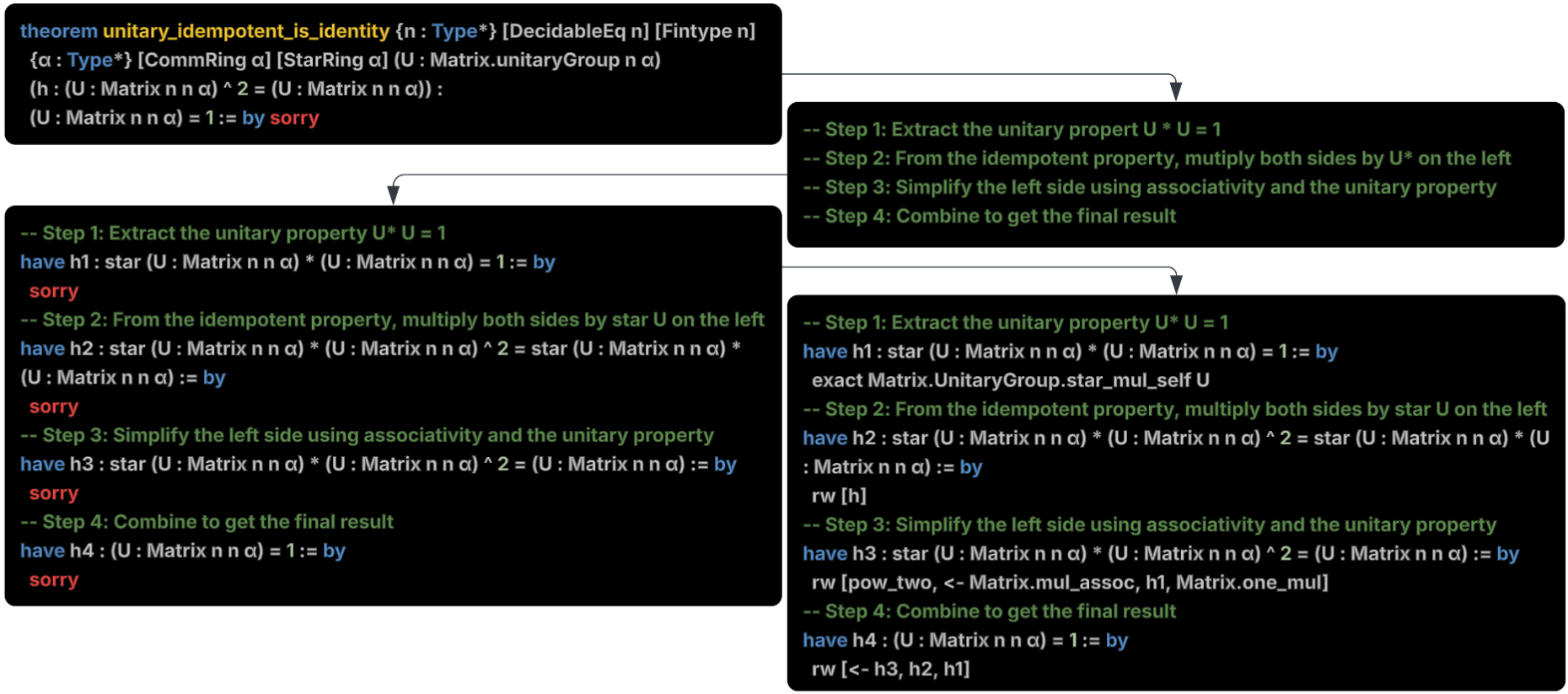
Figure 2: The main steps performed by the Prover to prove a theorem.

Tool integration is central to Ax-Prover’s architecture. The MCP interface exposes a suite of Lean tools for file management, diagnostics, code assistance, and theorem search, enabling the agents to operate on the latest Mathlib version and adapt to evolving libraries without retraining.

Datasets and Benchmarking

Ax-Prover is evaluated on four datasets:

• NuminaMath-LEAN: 104k competition-level math problems in Lean, stratified by difficulty and source (human or autoformalized).
• AbstractAlgebra (AA): 100 research-level problems from standard algebra texts, emphasizing deep conceptual reasoning.
• QuantumTheorems (QT): 134 problems in quantum mechanics, integrating linear algebra, complex analysis, and quantum postulates.
• PutnamBench: 660 undergraduate competition problems, serving as a high-value testbed for state-of-the-art provers.

The AA and QT datasets are newly introduced, targeting domains underrepresented in existing benchmarks and enabling evaluation of cross-disciplinary formal reasoning.

Experimental Results

Ax-Prover is benchmarked against Claude Sonnet 4 (general-purpose LLM), DeepSeek-Prover-V2-671B, and Kimina-Prover-72B (specialized Lean provers). Pass@1 is used for all models, reflecting practical constraints on repeated attempts.

NuminaMath-LEAN: Ax-Prover achieves 51% accuracy, outperforming DeepSeek-Prover (28%) and Kimina (31%), with Claude Sonnet at 5%. On the hardest subset (Unsolved), Ax-Prover solves 26% of problems, demonstrating robustness to ill-posed statements via early contradiction detection.

AbstractAlgebra: Ax-Prover attains 64% accuracy, exceeding DeepSeek-Prover (24%) and Kimina (13%) by a substantial margin. The performance gap is attributed to the out-of-distribution nature of AA for specialized models.

QuantumTheorems: Ax-Prover achieves 96% overall accuracy (100% on easy, 92% on intermediate), surpassing DeepSeek-Prover (61%) and Kimina (57%). The system demonstrates systematic, type-theoretic reasoning and effective use of library theorems, outperforming models that rely on shortcut tactics.

PutnamBench: Ax-Prover ranks third (14% accuracy, pass@1), behind Hilbert (72%, avg. pass@1840) and Seed-Prover (51%, medium parallelization). Notably, Ax-Prover’s result is obtained at a fraction of the computational cost, highlighting efficiency and accessibility.

Tool Usage and Deployment Analysis

Ax-Prover’s agentic workflow is characterized by frequent and autonomous tool calls—averaging over 100 per run on challenging problems. The most used tools are edit_file, lean_diagnostic_messages, lean_goal, and theorem search utilities. The system employs a broader set of Lean tactics than specialized models, supporting greater creativity and adaptability.

Deployment analysis reveals that specialized provers require high-spec GPU infrastructure and significant MLOps expertise, with prohibitive costs for large-scale or parallelized runs. Ax-Prover, by contrast, operates via API calls and can be executed locally or in lightweight containers, lowering barriers to adoption and reproducibility.

Researcher Collaboration and Use Cases

Ax-Prover is designed for interactive collaboration with human researchers, supporting verification of intermediate steps, structured feedback, and guided proof strategies. In a case paper, Ax-Prover assisted in formalizing and verifying a cryptography theorem, identifying a critical error in the original proof and producing a 2000-line Lean certificate in two days on a standard laptop. This contrasts with multi-week, multi-agent efforts required for comparable formalizations in prior work.

In quantum cryptography, Ax-Prover enabled machine-checked proofs of foundational results (e.g., Lo–Chau’s entropy bound), facilitating compositional security arguments in QKD and bridging formal reasoning with quantitative quantum information theory.

Implications and Future Directions

Ax-Prover demonstrates that agentic workflows, integrating general-purpose LLMs with formal toolchains, can overcome the domain rigidity and deployment challenges of specialized provers. The system’s superior generalization, tool-driven creativity, and collaborative capabilities position it as a candidate for deep formal reasoning assistants in scientific AI.

Future work includes parallelizing agentic exploration for increased creativity and success rates, integrating long-term memory for sustained research collaboration, and extending evaluation to additional scientific domains. These developments aim to advance verifiable scientific AI, where formal validation is integral to discovery and application.

Conclusion

Ax-Prover represents a significant advance in agentic theorem proving, combining multi-agent orchestration, tool-enhanced reasoning, and domain generalization. Its performance across mathematics and quantum physics benchmarks, efficient deployment, and collaborative utility underscore the potential of agentic LLM frameworks for rigorous, cross-disciplinary scientific reasoning. The introduction of new datasets and demonstration of practical use cases further establish Ax-Prover as a versatile platform for formal verification in evolving research landscapes.