Beyond Log Likelihood: Probability-Based Objectives for Supervised Fine-Tuning across the Model Capability Continuum (2510.00526v1)

Abstract: Supervised fine-tuning (SFT) is the standard approach for post-training LLMs, yet it often shows limited generalization. We trace this limitation to its default training objective: negative log likelihood (NLL). While NLL is classically optimal when training from scratch, post-training operates in a different paradigm and could violate its optimality assumptions, where models already encode task-relevant priors and supervision can be long and noisy. To this end, we study a general family of probability-based objectives and characterize their effectiveness under different conditions. Through comprehensive experiments and extensive ablation studies across 7 model backbones, 14 benchmarks, and 3 domains, we uncover a critical dimension that governs objective behavior: the model-capability continuum. Near the model-strong end, prior-leaning objectives that downweight low-probability tokens (e.g., $-p$, $-p^{10}$, thresholded variants) consistently outperform NLL; toward the model-weak end, NLL dominates; in between, no single objective prevails. Our theoretical analysis further elucidates how objectives trade places across the continuum, providing a principled foundation for adapting objectives to model capability. Our code is available at https://github.com/GaotangLi/Beyond-Log-Likelihood.

• The paper introduces probability-based objectives that leverage strong model priors to refine predictions and outperform negative log likelihood in Model-Strong settings.
• It demonstrates that NLL remains effective in Model-Weak scenarios while highlighting the need for adaptive strategies in Model-Intermediate cases.
• Experiments in domains such as mathematical and medical reasoning validate the continuum approach, offering actionable insights for fine-tuning large language models.

Beyond Log Likelihood: Probability-Based Objectives for Supervised Fine-Tuning across the Model Capability Continuum

Introduction

The paper addresses limitations in the traditional approach of using negative log likelihood (NLL) as the objective for supervised fine-tuning (SFT) of LLMs. It proposes probability-based objectives as a more effective alternative, particularly when the models have been pre-trained on vast datasets, already encoding substantial prior knowledge.

Model-Capability Continuum

The effectiveness of different objectives depends on the model-capability continuum—a spectrum defining model strength based on how well pre-trained models can leverage prior knowledge. This continuum is divided into three categories:

1. Model-Strong (MS) End: Models in this category have strong prior knowledge. Probability-based objectives that down-weight low-probability tokens, such as $-p$ and $-p^{10}$, significantly outperform NLL.
2. Model-Weak (MW) End: For models with weak priors, NLL remains favorable due to its ability to broadly learn from all tokens.
3. Model-Intermediate (MI) Region: No single objective dominates, highlighting the need for adaptive approaches.

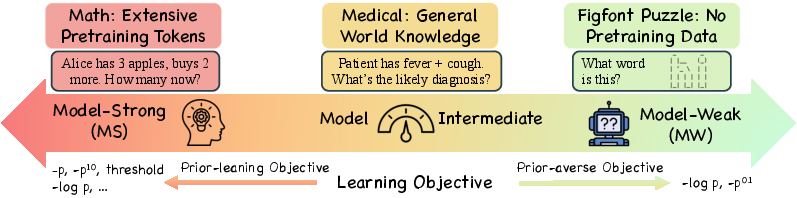
   Figure 1: The model capability continuum of SFT objectives in Post-Training. At the model-strong (MS) end, where base models already encode extensive priors, prior-leaning objectives consistently outperform NLL. The standard NLL dominates in the model-weak (MW) end.

Experimental Setup

The experiments validate the continuum view across domains like mathematical reasoning, medical reasoning, and textual puzzles. Various models, such as LLaMA-3.1-8B and Qwen2.5-Math-7B, were trained using AdamW with results showcasing distinct performance patterns along the continuum.

Main Experimental Results

Model-Strong End: In this scenario, $-p$ consistently outshines NLL by leveraging strong priors to make informed predictions, focusing on refining high-probability tokens and diminishing the influence of noise from low-probability predictions.

Model-Intermediate Results: There is no significant difference between $-p$ and NLL in medical reasoning tasks. This neutrality suggests that when priors are balanced, improvements in performance may depend more on other factors such as data quality.

Model-Weak End: NLL's emphasis on low-probability tokens helps correct errors by spreading learning broadly across predictions, essential in domains with weak prior support, such as textual puzzles.

Theoretical Insights

A theoretical analysis establishes the conditions under which prior-leaning and prior-averse objectives outperform each other. The paper shows that prior-leaning objectives excel when strong priors exist, while prior-averse objectives are preferable where priors are inadequate.

Conclusion and Future Directions

The paper suggests a shift from fixed objectives to adaptive strategies that cater to the model's prior knowledge, capable of dynamically evolving during training. Future work could focus on integrating domain-specific supervision and exploring curriculum-style adaptation techniques.

Figures for Visual Reference

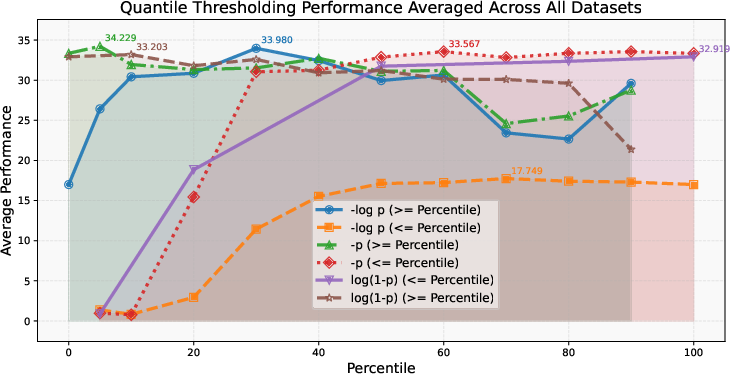
Figure 2: Performance under quantile thresholding for $-\log(p)$, $-p$, and $\log(1-p)$. $Q_{\text{percentile}}$ is the predicted probability threshold used for experimenting with the emphasis on probability ranges.

Figure 3: Analysis of MS and MW ends in terms of objective convexity and likelihood estimation. Highlights the contrasting performances of concave versus convex objectives across model capability spectrum.