On the Generalization of SFT: A Reinforcement Learning Perspective with Reward Rectification (2508.05629v1)

Abstract: We present a simple yet theoretically motivated improvement to Supervised Fine-Tuning (SFT) for the LLM, addressing its limited generalization compared to reinforcement learning (RL). Through mathematical analysis, we reveal that standard SFT gradients implicitly encode a problematic reward structure that may severely restrict the generalization capabilities of model. To rectify this, we propose Dynamic Fine-Tuning (DFT), stabilizing gradient updates for each token by dynamically rescaling the objective function with the probability of this token. Remarkably, this single-line code change significantly outperforms standard SFT across multiple challenging benchmarks and base models, demonstrating greatly improved generalization. Additionally, our approach shows competitive results in offline RL settings, offering an effective yet simpler alternative. This work bridges theoretical insight and practical solutions, substantially advancing SFT performance. The code will be available at https://github.com/yongliang-wu/DFT.

• The paper demonstrates that SFT overfits due to high-variance gradients from sparse, inverse-token probability rewards, motivating the need for a rectified approach.
• The paper introduces Dynamic Fine-Tuning (DFT), which dynamically reweights losses based on token probabilities to yield stable and uniformly weighted policy gradient updates.
• Empirical results show that DFT outperforms SFT and RL-based methods, achieving faster convergence and improvements of up to +15.66 points on challenging mathematical reasoning benchmarks.

Dynamic Fine-Tuning: A Reinforcement Learning Perspective on SFT Generalization

Introduction

This paper presents a rigorous theoretical and empirical investigation into the generalization limitations of Supervised Fine-Tuning (SFT) for LLMs, and introduces Dynamic Fine-Tuning (DFT) as a principled remedy. The authors demonstrate that SFT, when viewed through the lens of reinforcement learning (RL), implicitly encodes a reward structure that is both sparse and inversely proportional to the model's confidence in expert actions. This leads to high-variance gradients and overfitting, particularly in low-probability regions of the output space. DFT addresses this by dynamically reweighting the SFT loss with the model's own token probabilities, resulting in a stable, uniformly-weighted update mechanism. The empirical results show that DFT consistently outperforms SFT and even surpasses several RL-based fine-tuning methods on challenging mathematical reasoning benchmarks.

Theoretical Analysis: SFT as Policy Gradient with Implicit Reward

The core theoretical contribution is the formal equivalence between the SFT gradient and a policy gradient update with a specific, ill-posed reward structure. The SFT objective minimizes the negative log-likelihood of expert demonstrations, but its gradient can be rewritten as:

$$\nabla_\theta \mathcal{L}_{\mathrm{SFT}} = -\mathbb{E}_{x\sim\mathcal D_x,\,y\sim\pi_\theta(\cdot|x)} \left[ \frac{\mathbf{1}[y=y^*]}{\pi_\theta(y|x)} \nabla_\theta \log \pi_\theta(y|x) \right]$$

This is equivalent to a policy gradient with reward $r(x, y) = \mathbf{1}[y = y^*]$ and importance weight $1/\pi_\theta(y|x)$. The sparsity of the reward (nonzero only for exact matches) and the unbounded nature of the importance weight when $\pi_\theta(y^*|x)$ is small, result in high-variance, unstable updates. This explains SFT's tendency to overfit and its poor generalization compared to RL methods that use denser or more informative reward signals.

Dynamic Fine-Tuning: Reward Rectification via Dynamic Reweighting

DFT is introduced as a direct solution to the identified pathology. The method modifies the SFT loss by multiplying each token's loss by its own model probability (with stop-gradient to prevent gradient flow through the scaling term):

$$\mathcal{L}_{\mathrm{DFT}} = \mathbb{E}_{(x, y^*) \sim \mathcal{D}} \left[ -\sum_{t=1}^{|y^*|} \operatorname{sg}(\pi_\theta(y^*_t|y^*_{<t}, x)) \log \pi_\theta(y^*_t|y^*_{<t}, x) \right]$$

This simple modification cancels the problematic inverse-probability weighting, resulting in a stable, unbiased, and uniformly-weighted update. Theoretically, this aligns the SFT update with a policy gradient using a uniform reward for all expert trajectories, eliminating the over-concentration on rare, low-probability tokens.

Empirical Results: Robust Generalization and Efficiency

Main SFT Experiments

DFT is evaluated on multiple state-of-the-art LLMs (Qwen2.5-Math-1.5B/7B, LLaMA-3.2-3B, LLaMA-3.1-8B, DeepSeekMath-7B) and a suite of mathematical reasoning benchmarks (Math500, Minerva Math, Olympiad Bench, AIME24, AMC23). Across all models and datasets, DFT yields substantial improvements over both the base models and SFT. For example, on Qwen2.5-Math-1.5B, DFT achieves an average gain of +15.66 points over the base model, compared to +2.09 for SFT—a nearly 6x improvement. DFT also demonstrates resilience on challenging datasets where SFT degrades performance, such as Olympiad Bench and AIME24.

DFT exhibits superior learning efficiency, achieving faster convergence and higher sample efficiency than SFT. The accuracy progression curves show that DFT reaches peak performance within the first 120 training steps and often surpasses SFT's best final accuracy within the first 10–20 steps.

Figure 1: Accuracy progression for Qwen2.5-MATH-1.5B across mathematical benchmarks, illustrating faster convergence and better performance achieved by DFT relative to SFT.

Token Probability Distribution Analysis

A detailed analysis of token probability distributions reveals that SFT uniformly increases token probabilities, primarily targeting low-probability tokens, while DFT induces a bimodal distribution—boosting some tokens and suppressing others. This suggests that DFT encourages the model to focus on semantically meaningful tokens and deprioritize grammatical or connective tokens, potentially contributing to its improved generalization.

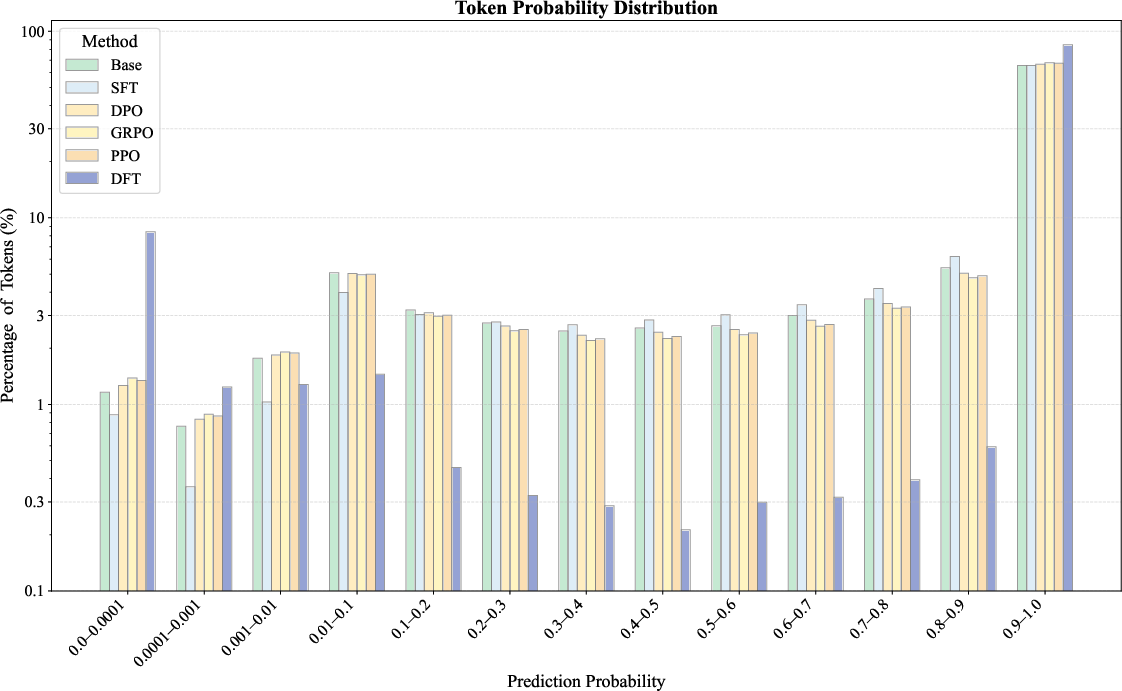
Figure 2: Token probability distributions on the training set before training and after fine-tuning with DFT, SFT, and various RL methods including DPO, PPO, and GRPO. A logarithmic scale is used on the y-axis to improve visualization clarity.

Hyperparameter Robustness

An ablation paper on learning rate and batch size demonstrates that DFT consistently outperforms SFT across a wide range of hyperparameter settings. Both methods are sensitive to learning rate, with intermediate values yielding the best results, but batch size has minimal impact on final accuracy.

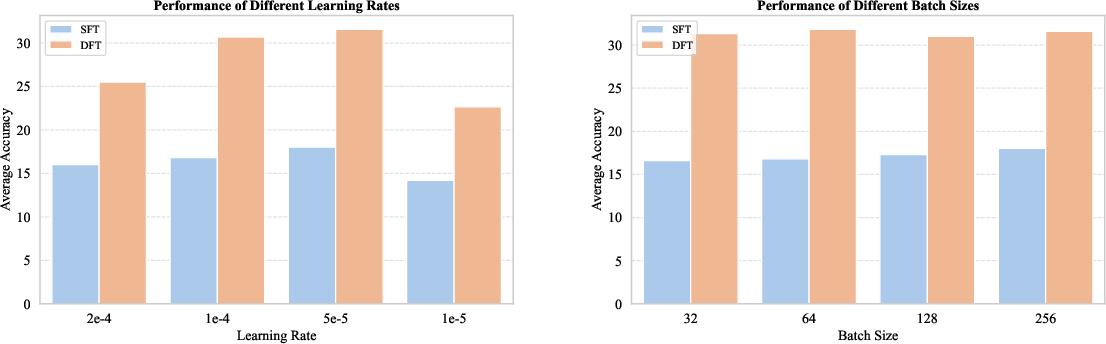
Figure 3: Ablation paper of training hyper-parameters, learning rates and batch size, for DFT and SFT on Qwen2.5-Math-1.5B model.

Offline RL Setting

DFT is further evaluated in an offline RL setting, where reward signals are available via rejection sampling. DFT outperforms both offline (DPO, RFT) and online (PPO, GRPO) RL baselines, achieving the highest average accuracy across all benchmarks. Notably, DFT surpasses the best online RL method (GRPO) by +3.43 points and the best offline method (RFT) by +11.46 points, despite its simplicity and lack of iterative reward modeling.

Practical Implications and Future Directions

The findings have significant implications for LLM post-training. DFT provides a theoretically grounded, computationally efficient, and empirically validated alternative to both SFT and RL-based fine-tuning, especially in settings where only positive expert demonstrations are available. The method is trivial to implement (a one-line change to the loss function), requires no additional models or reward signals, and is robust to hyperparameter choices.

Theoretically, the work clarifies the connection between SFT and RL, highlighting the importance of reward structure and variance in policy optimization. Practically, DFT offers a scalable solution for improving generalization in LLMs, particularly for tasks with sparse or ill-defined rewards.

Future research should explore the applicability of DFT to other domains (e.g., code generation, commonsense reasoning), larger model scales, and multimodal settings. Further investigation into the interaction between DFT and other alignment techniques, as well as its integration with hybrid SFT-RL pipelines, is warranted.

Conclusion

This paper provides a rigorous theoretical and empirical analysis of the generalization limitations of SFT for LLMs, identifying the implicit reward structure as the root cause of overfitting and instability. The proposed DFT method rectifies this by dynamically reweighting the loss with token probabilities, resulting in stable, robust, and efficient fine-tuning. Extensive experiments demonstrate that DFT consistently outperforms SFT and several RL-based methods across challenging mathematical reasoning tasks. The simplicity, effectiveness, and theoretical grounding of DFT make it a compelling alternative for LLM post-training, with broad implications for future research and deployment.