Pretrain-Test Task Alignment Governs Generalization in In-Context Learning (2509.26551v1)

Abstract: In-context learning (ICL) is a central capability of Transformer models, but the structures in data that enable its emergence and govern its robustness remain poorly understood. In this work, we study how the structure of pretraining tasks governs generalization in ICL. Using a solvable model for ICL of linear regression by linear attention, we derive an exact expression for ICL generalization error in high dimensions under arbitrary pretraining-testing task covariance mismatch. This leads to a new alignment measure that quantifies how much information about the pretraining task distribution is useful for inference at test time. We show that this measure directly predicts ICL performance not only in the solvable model but also in nonlinear Transformers. Our analysis further reveals a tradeoff between specialization and generalization in ICL: depending on task distribution alignment, increasing pretraining task diversity can either improve or harm test performance. Together, these results identify train-test task alignment as a key determinant of generalization in ICL.

• The paper presents an explicit alignment measure that quantifies the impact of pretraining task information on in-context learning generalization.
• It rigorously derives an exact high-dimensional expression linking pretrain-test covariance mismatch with ICL error using linear regression and linear attention.
• Empirical validation shows that the alignment measure robustly predicts generalization error in nonlinear Transformers, guiding optimal pretraining curricula.

Pretrain-Test Task Alignment Governs Generalization in In-Context Learning

Introduction and Motivation

This paper presents a rigorous theoretical and empirical analysis of how the alignment between pretraining and test task distributions governs generalization in in-context learning (ICL) for Transformer models. The authors focus on a solvable model: ICL of linear regression using linear attention, and derive an exact high-dimensional expression for ICL generalization error under arbitrary pretrain-test covariance mismatch. The central contribution is the identification and validation of a new alignment measure that quantifies the utility of pretraining task information for test-time inference, and the demonstration that this measure robustly predicts ICL performance in both linear and nonlinear Transformer architectures.

Model Setup and Analytical Framework

The analysis is grounded in a linear regression ICL task, where the model receives a context sequence $\{x_1, y_1, \ldots, x_\ell, y_\ell, x_{\ell+1}\}$ and must predict $y_{\ell+1}$, with $y_i = \langle x_i, w \rangle + \epsilon_i$. Pretraining consists of $n$ such contexts, each associated with a task vector $w^\mu$ sampled from a distribution with covariance $train$, and test-time tasks are drawn from a potentially different covariance $test$. The linear attention model is reduced to an analytically tractable form, enabling explicit computation of the optimal parameter matrix $\Gamma^*$ via ridge regression in the high-dimensional limit.

The key data parameters are token dimension $d$, context length $\ell$, pretraining batch size $n$, and task diversity $k$, with proportional scaling $\alpha = \ell/d$, $\tau = n/d^2$, $\kappa = k/d$. The analysis leverages random matrix theory to characterize the sample covariance $R_k$ and its deterministic equivalents $F_\kappa(z)$ and $\mathcal{M}_\kappa(z)$, which encode the recoverable signal from finite pretraining samples.

Main Theoretical Results: Alignment Measure and Generalization Error

The principal result is an explicit formula for the ICL test error in terms of pretraining and test covariances, context length, batch size, and task diversity:

$\mathcal{E}_\mathrm{ICL}(\Gamma^*) \simeq e_{\text{scalar}(\bm{\lambda}_\mathrm{train},test) + misalign(train,test)$

where the misalignment term is

$$misalign(train,test) = \langle test,\,\, \mathcal{K} \rangle$$

with

$$\mathcal{K} \equiv qF_\kappa(\sigma) + (q\tilde{\lambda}-\sigma^2)F'_\kappa(\sigma)$$

and $\tilde{\lambda}$, $\sigma$ are self-consistently defined by the data parameters and pretraining covariance. This alignment measure generalizes classical notions of covariate shift and spectral bias in kernel regression, capturing both eigenvector and eigenvalue mismatches as well as finite-sample effects.

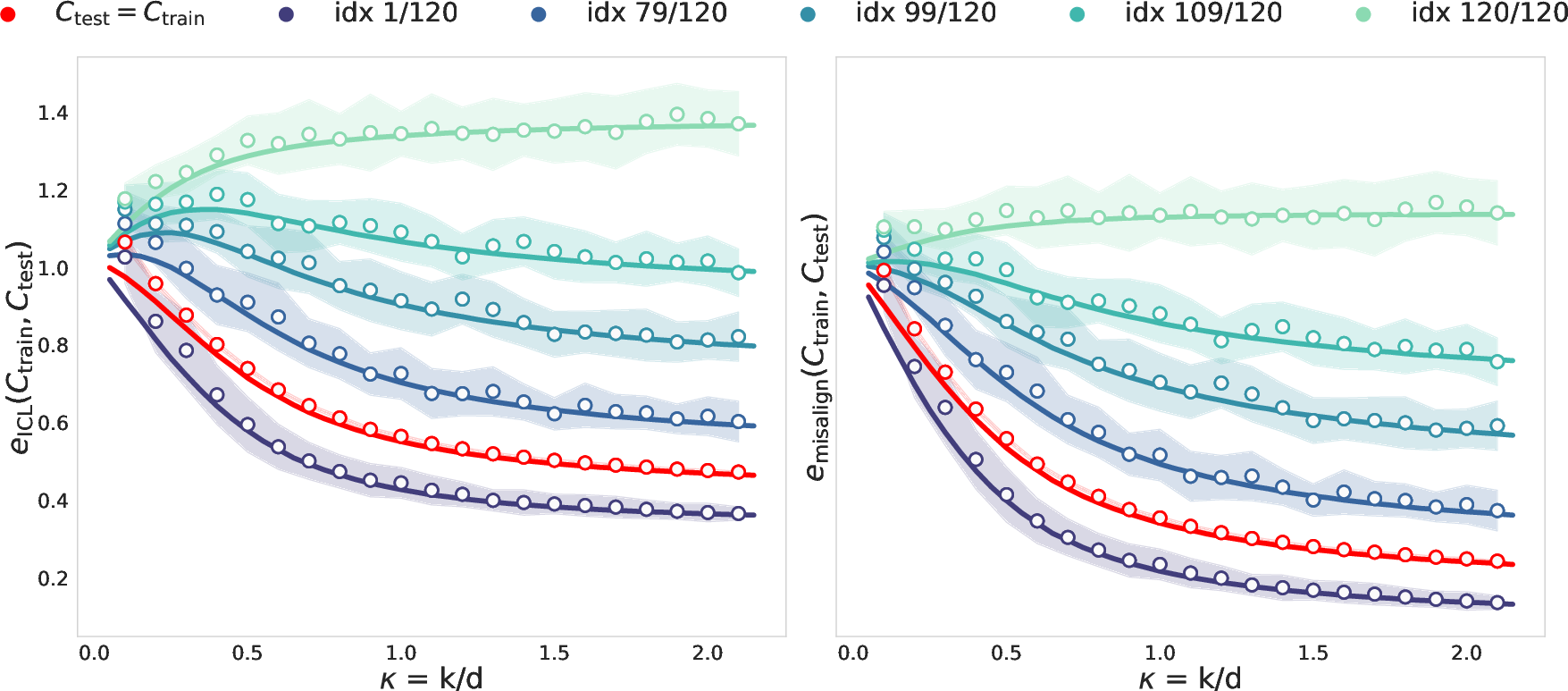
Figure 1: Theoretical ICL and misalign curves compared to numerical simulations, illustrating the dependence of generalization error on pretrain-test alignment and task diversity $\kappa$.

The analysis reveals that ICL error is not always minimized by matching pretraining and test distributions; rather, the optimal pretraining curriculum may involve deliberate misalignment, especially under limited task diversity. The misalignment term is shown to be a monotonic predictor of ICL error, outperforming alternative measures such as $\langle test\, train^{-1} \rangle$ and Centered Kernel Alignment (CKA).

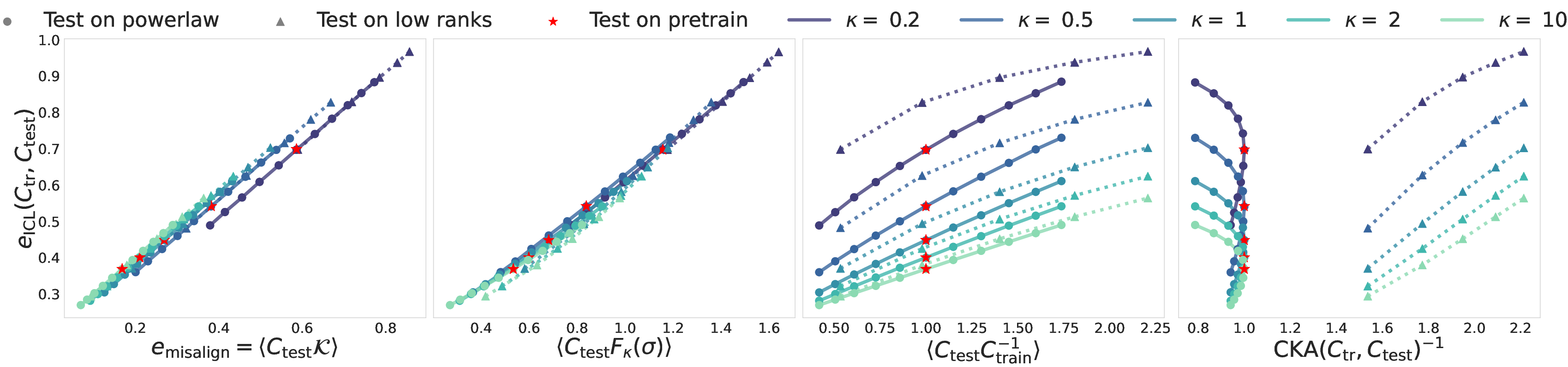
Figure 2: ICL error plotted against various alignment measures, demonstrating the superior predictive power of the proposed misalign metric across a range of test covariances.

Empirical Validation in Nonlinear Transformers

The alignment measure, derived for linear attention, is empirically validated in nonlinear Transformer architectures with softmax attention and MLP layers. The monotonic relationship between misalign and ICL error persists, with Spearman correlation coefficients exceeding 0.99, indicating that the theoretical insights extend beyond the linear regime.

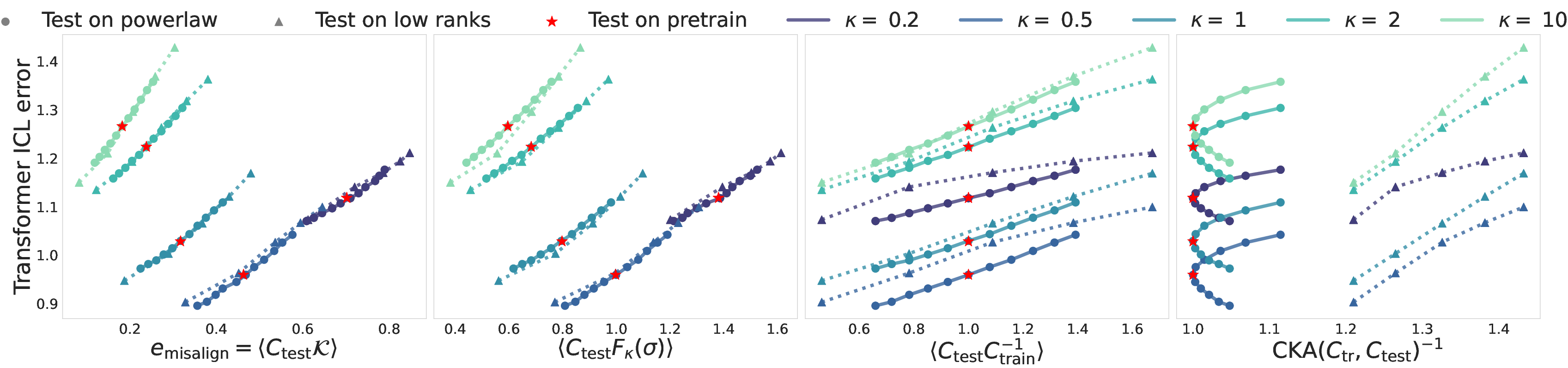
Figure 3: ICL test loss of a nonlinear Transformer versus alignment measures, confirming the robustness of the misalign metric in predicting generalization error.

Trade-offs: Specialization, Generalization, and Task Diversity

A central claim of the paper is that increasing pretraining task diversity $\kappa$ does not universally improve ICL performance; its effect depends critically on pretrain-test alignment. For well-aligned distributions, higher diversity reduces error, but for misaligned cases, it can be detrimental. The authors rigorously prove that the misalignment error is extremized when pretraining and test covariances are co-diagonalizable, and that the optimal test covariance for fixed pretraining is often low-rank and highly aligned with the dominant pretraining directions.

Moreover, the paper demonstrates that pretraining on a distribution with higher spectral power (i.e., more concentrated signal) than the test distribution can yield lower ICL error when task diversity is limited, but this advantage diminishes as $\kappa$ increases.

Figure 4: Heatmap of theoretical ICL error for powerlaw task covariances, showing that increased spectral power in pretraining can markedly improve generalization under low task diversity.

Phase Transitions and Scaling Behavior

The analysis recovers and generalizes known phase transitions in ICL as a function of task diversity, showing that the transition point depends on the rank of the pretraining covariance. The error exhibits a sharp drop when $\kappa$ exceeds the effective rank, consistent across a variety of test structures.

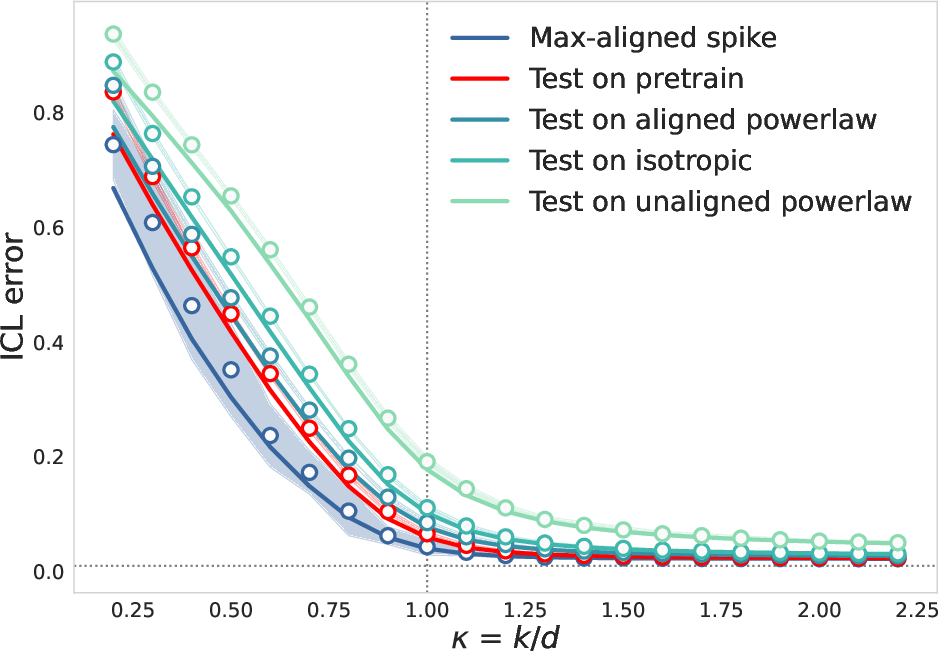
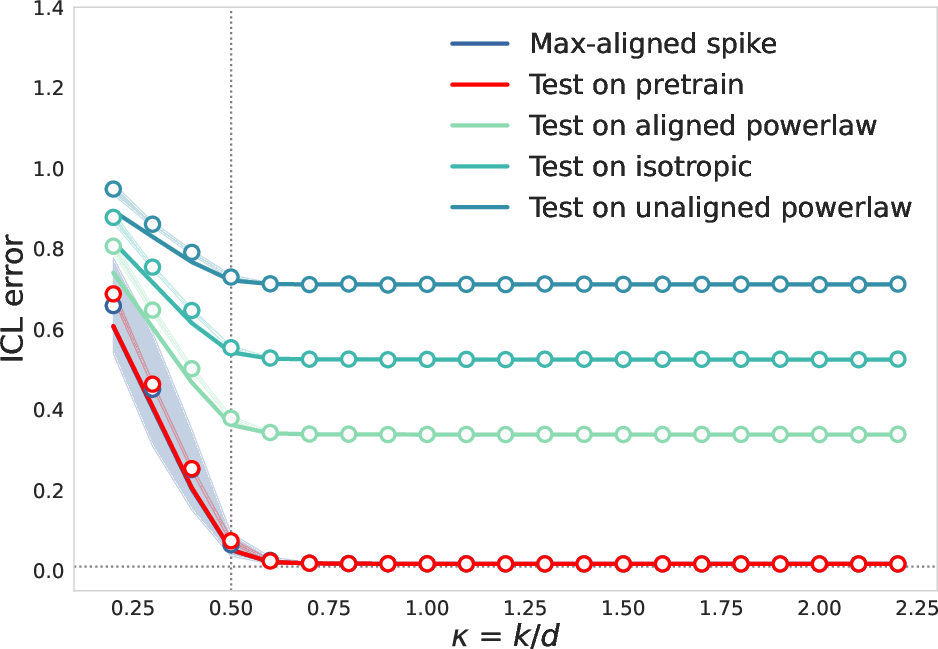
Figure 5: Full-rank phase transition in ICL error as a function of task diversity $\kappa$.

Additionally, the paper establishes that increasing test-time context length monotonically decreases ICL error, as longer contexts provide better estimates of the underlying token distribution.

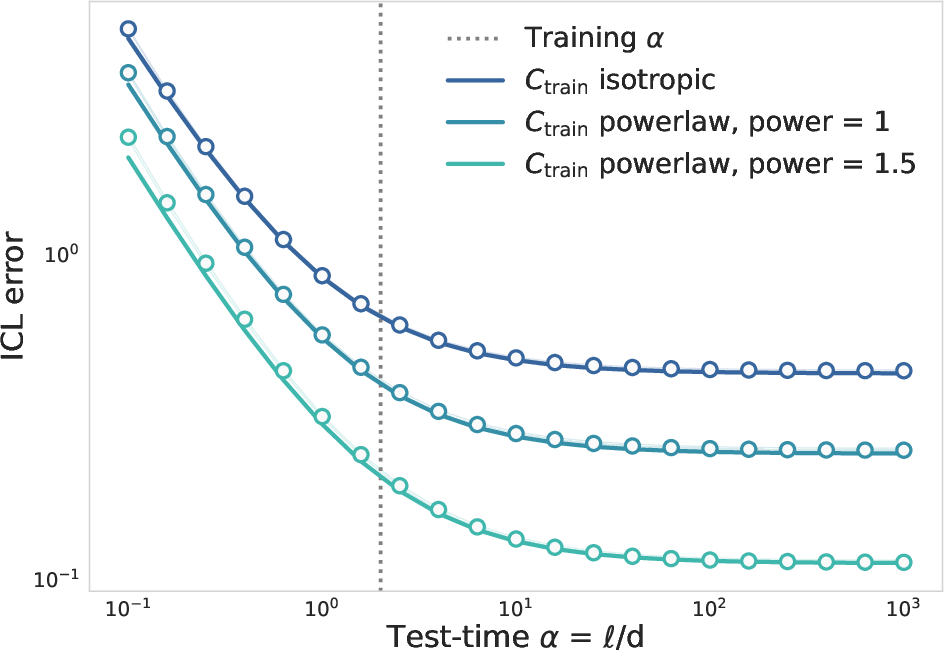
Figure 6: Monotonic decrease of ICL error with increasing test-time context length, across different task structures.

Implications and Future Directions

The findings have significant implications for the design of pretraining curricula and the deployment of in-context learners. The identification of a precise alignment measure enables principled selection of pretraining tasks to optimize generalization for anticipated test distributions. The results challenge the conventional wisdom of "teaching to the test," suggesting that, under certain regimes, optimal generalization requires intentional misalignment and specialization.

The theoretical framework opens avenues for further research, including the derivation of heuristics for optimal pretraining under resource constraints, exploration of learning transitions in task diversity, and investigation of test-time adaptation strategies. The extension of these results to more complex, structured tasks and broader model classes remains an important direction.

Conclusion

This work provides a comprehensive theoretical and empirical account of how pretrain-test task alignment governs generalization in in-context learning. The derived alignment measure is shown to be a robust predictor of ICL performance, even in nonlinear Transformer architectures, and the analysis elucidates nuanced trade-offs between specialization and generalization. The results inform both the theory and practice of meta-learning with Transformers, highlighting the critical role of task structure and diversity in shaping emergent learning algorithms.