Knapsack RL: Unlocking Exploration of LLMs via Optimizing Budget Allocation (2509.25849v1)
Abstract: LLMs can self-improve through reinforcement learning, where they generate trajectories to explore and discover better solutions. However, this exploration process is computationally expensive, often forcing current methods to assign limited exploration budgets to each task. This uniform allocation creates problematic edge cases: easy tasks consistently succeed while difficult tasks consistently fail, both producing zero gradients during training updates for the widely used Group Relative Policy Optimization (GRPO). We address this problem from the lens of exploration budget allocation. Viewing each task's exploration as an "item" with a distinct "value" and "cost", we establish a connection to the classical knapsack problem. This formulation allows us to derive an optimal assignment rule that adaptively distributes resources based on the model's current learning status. When applied to GRPO, our method increases the effective ratio of non-zero policy gradients by 20-40% during training. Acting as a computational "free lunch", our approach could reallocate exploration budgets from tasks where learning is saturated to those where it is most impactful. This enables significantly larger budgets (e.g., 93 rollouts) for especially challenging problems, which would be computationally prohibitive under a uniform allocation. These improvements translate to meaningful gains on mathematical reasoning benchmarks, with average improvements of 2-4 points and peak gains of 9 points on specific tasks. Notably, achieving comparable performance with traditional homogeneous allocation would require about 2x the computational resources.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper is about teaching LLMs—like the ones that help solve math problems—to learn better using reinforcement learning (RL). The main idea is simple: when the model practices, it has a limited “try” budget (how many answers it can generate per question). Instead of giving every question the same number of tries, the paper shows how to smartly split this budget so hard questions get more tries and easy ones get fewer. They use a classic “backpack” (knapsack) idea from math: your backpack has limited space, so pick items that give you the most value for their weight.
Key Questions
The paper asks:
- How can we use a fixed amount of computing power (the try budget) in a smarter way during training?
- Why do some common training methods fail to learn from very easy or very hard questions?
- Can we improve learning by giving different numbers of tries to different questions?
- What’s a good rule to decide how many tries each question should get?
Methods and Approach
Think of training the model like studying for a test with limited time:
- Exploration means “trying different ways to answer” (the model generates several responses per question).
- Exploitation means “using what you learned to do better next time” (updating the model based on feedback).
- A “rollout” is one try: the model writes a solution and gets checked if it’s correct.
A common RL method they use is called GRPO. GRPO learns best when, for a given question, the batch of tries contains some correct and some incorrect answers. That mixture gives a strong learning signal (called a “gradient”). If all tries are correct or all are incorrect for a question, GRPO gets almost no signal—like trying to improve with no feedback.
Here’s the problem with giving the same number of tries to every question:
- Easy questions often end up with all-correct tries.
- Hard questions often end up with all-wrong tries.
- In both cases, GRPO gets a zero learning signal and can’t improve from those questions.
To fix this, the authors treat each question like an “item” you might pack into a backpack:
- Cost = how many tries you give the question.
- Value = how much that helps learning.
- The backpack (computer) has a fixed capacity (total tries you can afford).
They then use a knapsack optimization to pick how many tries each question gets, aiming to maximize total learning value while staying within the overall budget.
Key ideas made simple:
- Success rate p: the chance the model solves a question correctly right now.
- Probability of getting a useful learning signal for a question with N tries is roughly:
- This is high when you’re likely to get a mix of correct and incorrect tries.
- Information gain: how much the model is expected to improve on that question after learning. They use a simple formula that depends on p and favors questions that are neither too easy nor too hard.
How they make it work in practice:
- Estimate each question’s current success rate p using recent training data.
- Use a fast knapsack solver to assign different numbers of tries to different questions.
- Always keep a small minimum number of tries for every question so none are ignored.
- If many questions become easy later in training, they shift saves tries to the hard ones.
Main Findings
Here are the most important results from their experiments on math and science benchmarks:
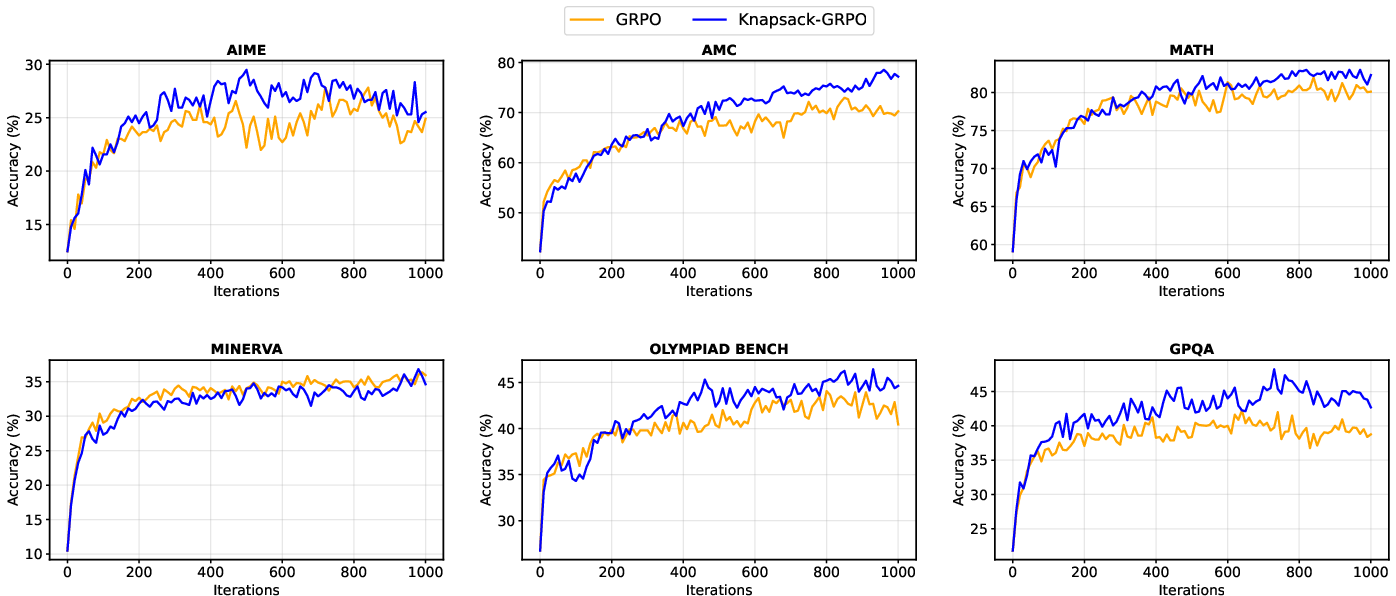
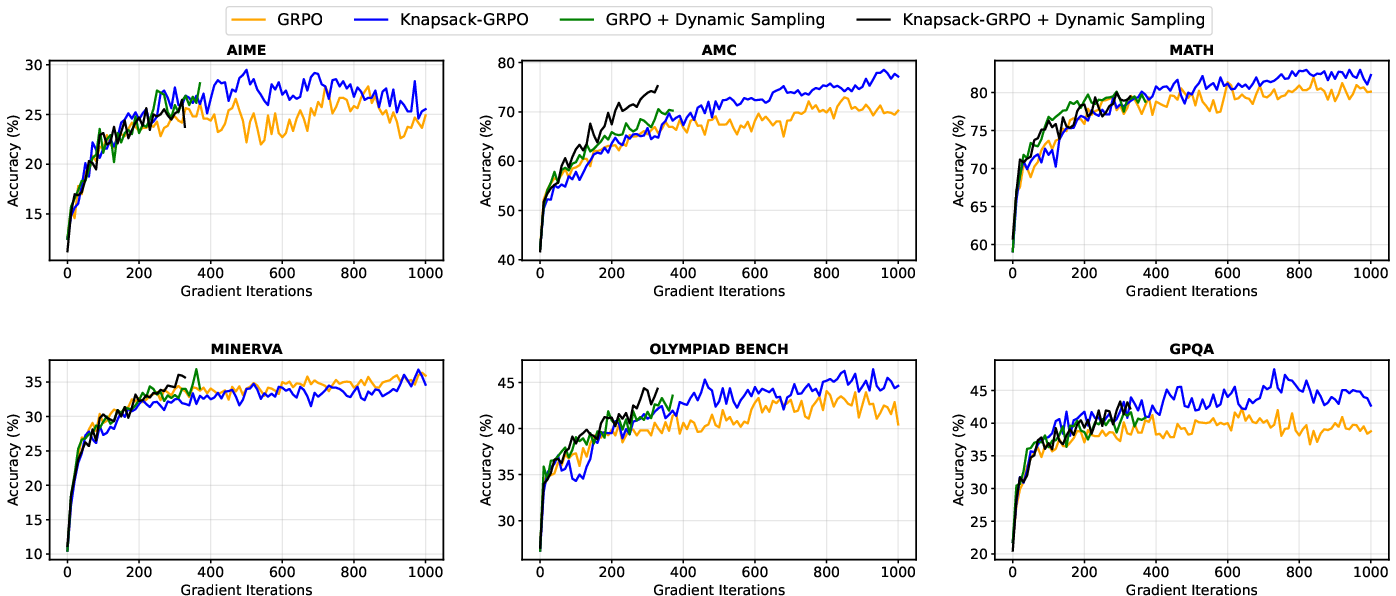
- More useful learning signals: The share of tries that actually help the model learn (the “effective gradient ratio”) increased by about 20–40% during training.
- Better scores: Average scores improved by around 2–4 points across several tests, with up to 9-point gains on some specific tasks (like AMC and AIME).
- Same performance with half the compute: To match their results using the old “same tries per question” method, you’d need roughly 2× more computing.
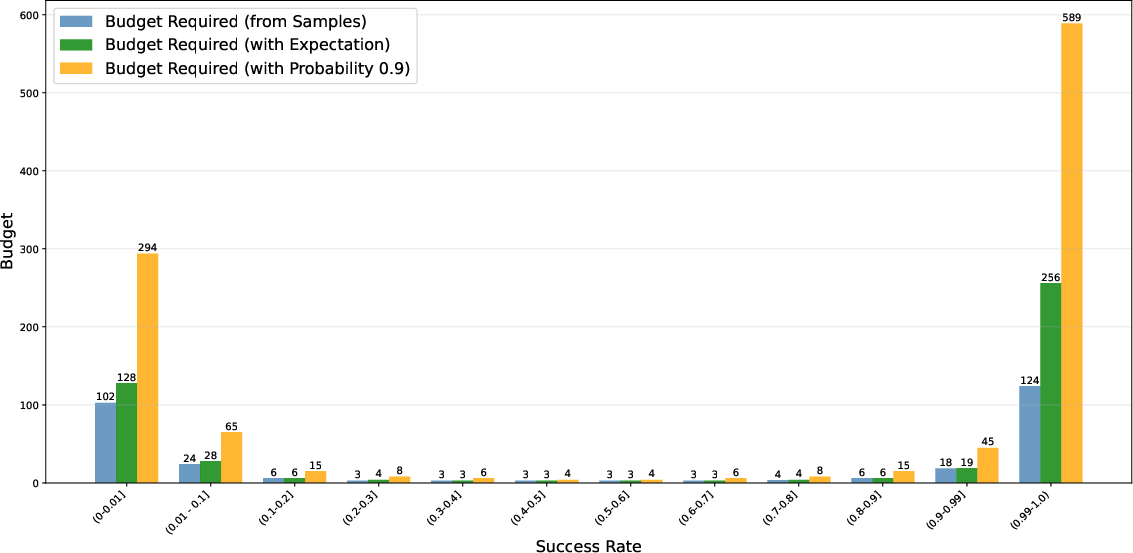
- Smarter budgets: Their method could give very hard questions up to 93 tries when needed, without increasing the total budget. This would be too expensive under the uniform approach.
- Works across models: Improvements were seen on different model sizes and families (e.g., Qwen and DeepSeek variants).
Why This Matters
- Efficiency: You get more learning out of the same amount of compute. That’s like studying smarter, not longer.
- Fair learning: Hard questions get the attention they need, so the model keeps improving on challenging problems instead of coasting on easy ones.
- Better training stability: By ensuring more mixed outcomes per question, the training method avoids “no feedback” cases and keeps progressing.
- Broad impact: While tested on math and some science questions, this idea can extend to coding and other tasks where you can check if an answer is correct.
Conclusion and Impact
This paper shows a practical way to make RL training for LLMs more effective: don’t give every question the same number of tries. Instead, treat your total compute like a backpack and pack it with the most valuable “items” by assigning tries where they matter most. The result is better learning signals, better scores, and better use of resources—often matching the performance of traditional methods that would need twice the compute.
In simple terms: if you have a fixed budget of attempts, spend them wisely. This approach helps LLMs learn faster and more reliably, especially on tough problems, and could be a building block for training smarter AI systems in many areas.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a single, concrete list of what remains missing, uncertain, or unexplored in the paper. Each item is framed to enable actionable follow-up by future researchers.
- Formal optimality and convergence: There is no theoretical link between the proposed knapsack objective (maximizing Value(N_i, p_i)) and improvements in the RL objective in Eq. (1). Provide convergence guarantees or bounds showing that knapsack allocation increases expected return or sample efficiency relative to uniform GRPO.
- Gradient-quality modeling: The value function only captures the probability of obtaining non-zero gradients times an approximate “info gain,” but ignores expected gradient magnitude, direction quality, and variance (e.g., E[||g_i||], Fisher information). Derive and validate a value function that predicts actual training progress (e.g., expected policy improvement per unit compute).
- InfoGain approximation validity: The Taylor-based approximation is heuristic. Its derivation is undocumented in the main text, and its applicability to GRPO (with group baselines and normalization) is unproven. Empirically test and compare alternative proxies (e.g., advantage variance, gradient norm, entropy) and provide theoretical justification.
- Independence and Bernoulli assumptions: The analysis assumes independent Bernoulli rewards with stationary success rate , but LLM rollouts under common decoding strategies (temperature, nucleus sampling, seeds) are correlated. Quantify the impact of correlation on non-zero gradient probabilities and revise theory accordingly.
- Non-stationarity of : Success rates change rapidly during training. The current approach uses previous-epoch estimates , which can be stale. Develop online, uncertainty-aware estimators (e.g., Beta-Bernoulli posteriors, Kalman filters, change-point detection) and knapsack formulations that incorporate confidence intervals or UCB-style exploration bonuses.
- Within-iteration adaptivity: Allocation is done per epoch, not within iterations. Investigate sequential, on-the-fly reallocation (racing/halting) where early partial outcomes trigger additional rollouts for promising prompts.
- Extreme-case handling is heuristic: The fallback for and minimum budgets for lack principled justification. Design and evaluate methods that treat these regimes explicitly (e.g., exploration bonuses, curricula, staged thresholds) and quantify their effect on forgetting and overfitting.
- Compute cost heterogeneity: The knapsack cost is “rollout count,” but rollout compute varies strongly across prompts (length, tool calls, external judges). Replace unit-cost budgets with token/FLOP-aware costs and evaluate whether compute-normalized allocation changes conclusions.
- System-level efficiency: The rollout balancing strategy may degrade vLLM prefix caching and GPU utilization for long prompts. Measure wall-clock throughput, idle rates, and end-to-end efficiency; explore cache-aware bin-packing or schedulers optimized for heterogeneous budgets.
- Scalability of the knapsack solver: The DP-based solver’s complexity and memory footprint for large M (e.g., 100k prompts), large , and wide are not analyzed. Provide complexity bounds, streaming/approximate solvers, or decomposition schemes.
- Bias and variance of the gradient estimator under heterogeneous sampling: Changing per-prompt sampling frequency implicitly alters the training distribution. Analyze whether Knapsack-GRPO remains unbiased or requires importance weighting; quantify variance effects and stability.
- Interplay with GRPO’s normalization (c_i = 1/(σ_i+ε)): The value function ignores how σ_i and group composition affect gradient scaling. Study how allocation influences σ_i, gradient stability, and learning dynamics.
- Overfitting and coverage: Allocating up to 93 rollouts to a small subset of prompts risks overfitting and reduced coverage. Track per-prompt overfitting, implement coverage constraints, and measure downstream generalization vs. specialization trade-offs.
- Catastrophic forgetting: Easy prompts receive minimal budgets (e.g., N_low=2), but forgetting is not assessed. Introduce safeguards or periodic rechecks to prevent drift on previously solved prompts and quantify retention.
- Hyperparameter sensitivity: No ablations for , , the epoch length of estimates, or status bin thresholds. Perform sensitivity analyses and provide practical guidelines for setting these parameters across datasets and models.
- Benchmarks and domains: Experiments mostly target math and a single OOD benchmark (GPQA). Validate generality on coding, logical reasoning, tool-using agents, and preference-based tasks to test whether gains transfer beyond verifiable binary rewards.
- Model scale: Results cover up to 7B parameters. Assess behavior and systems constraints (memory, throughput) at 30B–70B+ scales, and determine whether allocation policies need to change at larger model sizes.
- Alternative baselines: The paper does not compare against contemporary dynamic allocation/selection methods (e.g., DAPO’s dynamic sampling, RAFT/rejection-sampling allocation, curriculum learning, bandit-based adaptive N). Implement strong baselines to contextualize gains.
- Reward types beyond binary: The framework targets verifiable binary rewards. Extend to graded/numeric rewards, pairwise preferences (RLHF), sparse rewards, and noisy/ambiguous evaluators; redesign value functions accordingly.
- Decoding and sampling effects: Success rates depend on temperature, top-p, and sampling seeds. Optimize allocation jointly over decoding parameters and budgets, or include decoding choices in the “knapsack items.”
- Uncertainty-aware allocation: Incorporate estimator variance (e.g., wide confidence intervals for prompts with few observations) directly into the knapsack objective to avoid over/under-allocation due to noisy .
- Cross-prompt correlations: Prompts are not independent; many share structure or subskills. Use clustering/meta-features to predict and allocate at cluster-level; paper transfer where exploration on one prompt improves others.
- Token-level budget policies: Move beyond rollout counts to allocate token budgets, CoT length, number of self-consistency votes, tool invocations, or “thinking time” as distinct resource dimensions, and solve multi-dimensional knapsack variants.
- Theoretical characterization of when knapsack allocation is optimal: Identify conditions under which the proposed formulation maximizes learning progress (e.g., monotone value functions, submodularity) and when it may misallocate compute.
- Robustness to reward noise and checker errors: Binary verifiers (math solvers, code checkers) can be wrong. Analyze how reward noise biases estimates and devise robust allocation strategies (e.g., filtering, consensus checking).
- Fairness and starvation: Ensure no subset of prompts is persistently starved of exploration. Define fairness/coverage metrics and constraints, and examine long-term effects on diversity of learned skills.
- Experience replay for “unsolved” but solvable prompts: The paper notes many “extremely hard” prompts had occasional successes. Evaluate replay, prioritization, and curriculum mechanisms explicitly integrated with knapsack allocation.
- Train–test compute trade-offs: Quantify how train-time knapsack scaling interacts with test-time scaling (best-of-N, majority vote), and develop joint optimization strategies for a fixed overall compute budget.
- Reproducibility details: The paper lacks run-to-run variance, statistical significance tests, and seed/configuration disclosures. Provide comprehensive reproducibility artifacts (code, seeds, exact configs and hardware profiles) and uncertainty estimates for reported gains.
Practical Applications
Immediate Applications
The following items can be deployed now using the paper’s knapsack-based exploration allocator for RL with verifiable rewards (e.g., GRPO), with minimal engineering overhead and no additional compute.
- Software development (code generation with unit tests)
- Use case: In RL pipelines where code correctness is verifiable via unit tests, dynamically allocate rollouts to prompts near pass/fail boundaries to increase non-zero gradients and accelerate learning.
- Tools/workflows: Integrate a “Knapsack-GRPO” plugin into existing RLHF/RLAIF training stacks (e.g., Verl + vLLM + FSDP/Megatron). Add an MLOps dashboard tracking the effective-gradient-ratio and per-prompt success rates.
- Assumptions/dependencies: Requires automatic checkers (unit tests, static analysis, sandbox execution) and binary or near-binary reward signals. Success-rate estimates are computed from prior epochs.
- Education (mathematics reasoning tutors)
- Use case: Improve math LLMs (AIME/AMC/MATH-style benchmarks) by reallocating exploration budgets toward tasks with the highest expected info gain, achieving 2–4 average point improvements at constant compute.
- Tools/workflows: Drop-in replacement for homogeneous rollout counts in GRPO with knapsack DP. Batch-level rollout balancing to avoid GPU idle time.
- Assumptions/dependencies: Verifiable reward is available (ground-truth answers). Works best when prompts are of modest length or when caching/bin-packing is used.
- Agentic automation (task-oriented LLM agents with verifiable outcomes)
- Use case: Train web agents, form fillers, or API orchestration agents that receive binary success signals (e.g., “item acquired,” “form submitted”) by allocating more rollouts to borderline tasks rather than easy or impossible ones.
- Tools/workflows: Extend current GRPO-style agent training with a knapsack allocator; incorporate a rollout job queue that randomizes execution across workers.
- Assumptions/dependencies: Requires robust automatic validators for task completion; outcome reward must be reliably computed.
- Finance and data analytics (SQL/query correctness, data cleaning)
- Use case: Train LLMs to write correct SQL or cleaning rules where correctness is verifiable by executing queries/tests and comparing outputs with golden results; prioritize queries with mixed outcomes for maximal gradient yield.
- Tools/workflows: Connect the allocator to query validators in the pipeline; instrument effective-gradient-ratio as a training KPI.
- Assumptions/dependencies: Deterministic validators and access to ground-truth tables or checksums; binary reward or thresholds that approximate binary outcomes.
- MLOps and training efficiency (cluster-level utilization)
- Use case: Increase gradient effectiveness by 20–40% and cut cost (~50% to match the same performance) by replacing uniform rollout counts with knapsack-optimized budgets under the same total compute cap.
- Tools/workflows: A “budget-aware” scheduler that solves a small DP per epoch (Numba-accelerated) and dispatches per-prompt rollout jobs to workers to maintain utilization.
- Assumptions/dependencies: Stable success-rate estimation; compatibility with current inference engines; minor rollout balancing required.
- Open-source labs and small enterprises (cost-aware fine-tuning)
- Use case: Fine-tune small-to-mid LLMs (e.g., Qwen 1B–7B) on limited GPUs by reallocating exploration budgets to hard prompts rather than uniformly increasing N.
- Tools/workflows: A Python package providing
allocate_rollouts(p_i, N_total)and hooks for Verl/vLLM; prebuilt metrics for monitoring zero-gradient ratios by all-positive/all-negative groups. - Assumptions/dependencies: Binary rewards available; the value function matches GRPO (p·(1−p)2); minimal changes to the existing stack.
- Safety-aligned coding (linting/sandbox checks as rewards)
- Use case: Train models to avoid insecure patterns using binary verifiers (e.g., sandboxed execution, policy linting) by allocating exploration budgets to cases with mixed outcomes rather than extremes.
- Tools/workflows: Integrate knapsack allocation with secure code checkers and sandbox infrastructure.
- Assumptions/dependencies: High-quality verifiers; binary reward fidelity; careful fallback allocation for extremely hard/easy prompts.
- Research workflows (academia)
- Use case: Improve reproducibility and sample efficiency for RL research where verifiable rewards exist (math, algorithmic tasks, constrained planning). Report effective-gradient-ratio and budget distributions alongside accuracy.
- Tools/workflows: A research toolkit for systematic reporting (effective-gradient-ratio curves, transition matrices, final status distributions) to diagnose exploration quality.
- Assumptions/dependencies: Binary reward availability; accurate success-rate tracking; adequate logging.
Long-Term Applications
These items require further research, scaling, or development (e.g., new reward designs, generalized value functions, better estimation, domain-specific validators).
- RLHF/RLAIF with non-binary or human preference signals (product LLMs)
- Use case: Extend the knapsack allocator beyond binary rewards to preference-based feedback by redefining the “value” term to handle graded or noisy rewards and human rater variance.
- Tools/workflows: New info-gain proxies and confidence-aware success estimators; bandit-style variance modeling.
- Assumptions/dependencies: Reliable estimators of “learning value” under subjective feedback; policy-aware baselines; mitigation for human labeling latency.
- Robotics and simulation-based RL (industry/academia)
- Use case: Allocate episode budgets across tasks/goals/scenarios in high-cost simulators, prioritizing those with maximum learning value rather than uniform episode counts.
- Tools/workflows: Map episode cost to item “weight” and expected policy improvement to “value”; integrate with simulators and curriculum schedulers.
- Assumptions/dependencies: Verifiable objectives, task difficulty estimation, domain-consistent value approximations; handling long-horizon, continuous rewards.
- Carbon-aware compute governance (policy/energy)
- Use case: Couple knapsack allocation with energy-aware scheduling to respect carbon caps, allocating exploration budgets when grid intensity is low while preserving training efficacy.
- Tools/workflows: A carbon-aware allocator that treats energy/quota as knapsack capacity; reporting effective-gradient-ratio as an efficiency metric in compliance frameworks.
- Assumptions/dependencies: Access to energy telemetry and carbon intensity signals; cluster-level orchestration; policy buy-in for standardized efficiency metrics.
- Red-teaming and safety evaluation (security/policy)
- Use case: Allocate exploration to adversarial prompts most likely to produce informative failures, improving robustness testing and safety training.
- Tools/workflows: Adversarial prompt generators with automatic checkers; knapsack allocation to maximize failure-to-success conversion insights.
- Assumptions/dependencies: High-quality evaluators for safety policies; careful handling of harmful content; alignment oversight.
- AutoML and hyperparameter search (software/ML platforms)
- Use case: Treat candidate configurations as “items” and allocate trial budgets to those with highest expected improvement value under a global compute cap.
- Tools/workflows: Knapsack-driven trial schedulers; integration with Bayesian optimization/bandits; efficiency dashboards.
- Assumptions/dependencies: Good proxies for “value” (expected gain per trial); dynamic updates as results arrive; coordination with existing search algorithms.
- Budget-aware curriculum learning (education/software)
- Use case: Combine prompt selection with budget-aware exploration so that selected samples also get rollouts commensurate with their learning value, yielding a curriculum that optimizes both “which” and “how much.”
- Tools/workflows: Joint optimizer for sampling distribution and rollout budgets; curriculum visualizations (transition matrices).
- Assumptions/dependencies: Stable difficulty estimates; avoiding overfitting to narrow bands of p; balancing exploration vs. exploitation.
- Multi-tenant RL training services (cloud/SaaS)
- Use case: Offer “budget-optimized RL fine-tuning” to enterprise customers—meeting SLAs under fixed compute caps by maximizing effective-gradient-ratio and reallocating exploration away from saturated workloads.
- Tools/workflows: Tenant-aware knapsack allocators; rollout job queues; QoS/priority overlays.
- Assumptions/dependencies: Accurate per-tenant metrics; fairness policies; isolation and observability.
- Edge/on-device personalization (consumer/daily life)
- Use case: On-device micro-fine-tuning of assistants for tasks with verifiable outcomes (e.g., local code snippets, personal data queries), allocating limited rollouts intelligently to maximize learning under tight resource budgets.
- Tools/workflows: Lightweight DP allocator; local validators; fallback rules for extreme cases.
- Assumptions/dependencies: On-device validators and compute; privacy-preserving logging; energy constraints.
- Domain-specific validators (healthcare, law, engineering)
- Use case: Create automated checkers for narrowly scoped tasks (e.g., drug–dose math, legal citation formatting, engineering unit conversions) to unlock knapsack-based RL training in high-stakes domains.
- Tools/workflows: Validator development toolkits; reward design libraries; compliance wrappers.
- Assumptions/dependencies: High-fidelity validation pipelines; regulatory approval where needed; careful scoping to avoid unsafe generalization.
- Standardization and benchmarking (policy/academia)
- Use case: Adopt effective-gradient-ratio and zero-gradient ratios (all-positive/all-negative) as standard training efficiency metrics in benchmarks and reporting, driving industry-wide focus on exploration quality.
- Tools/workflows: Benchmark suites and reporting templates; third-party audits of training efficiency.
- Assumptions/dependencies: Community consensus; shared telemetry formats; alignment with emerging AI sustainability standards.
Glossary
- Autoregressive generation: Sequential token-by-token generation where each next token depends on previously generated tokens. "Exploration in RL is computationally expensive due to the sequential nature of autoregressive generation, often requiring substantial GPU memory and hours of computation, especially for reasoning tasks."
- Bernoulli random variables: Binary-valued random variables used to model success/failure outcomes. "We model reward outcomes as Bernoulli random variables to analyze the exploration budget required."
- Chain-of-Thought (CoT): Explicit intermediate reasoning steps included in model outputs to aid problem solving. "Chain-of-Thought (CoT) \citep{wei2022chain} reasoning steps"
- Dynamic programming: An algorithmic technique that solves optimization problems by breaking them into overlapping subproblems efficiently. "which can be solved in polynomial time using standard dynamic programming techniques."
- Effective-gradient-ratio: The proportion of sampled trajectories that produce non-zero gradients during training. "we introduce the metric effective-gradient-ratio, which measures the proportion of individual samples that contribute non-zero gradients:"
- Exploration budget: The amount of computational effort (e.g., number of rollouts) allocated to explore a task’s trajectories. "assign limited exploration budgets to each task."
- FSDP: Fully Sharded Data Parallel; a distributed training method that shards model states across devices to reduce memory. "training (e.g., FSDP \citep{zhao2023pytorch} and Megatron \citep{megatron-lm}) remain unchanged"
- GRPO (Group Relative Policy Optimization): A policy optimization method that computes advantages relative to responses within the same prompt group. "We adopt the widely used gradient estimator from Group Relative Policy Optimization (GRPO)"
- Indicator function: A function that returns 1 when a condition is true and 0 otherwise. "where is the indicator function and is binary (1 for correct, 0 for incorrect)."
- Information Gain (InfoGain): The expected increase in a prompt’s success probability due to a gradient update. "In this work, we define as a measure of the expected increase in success probability after a gradient update"
- Karmarkar–Karp bin-packing algorithm: A heuristic algorithm for partitioning items into balanced bins, used here for workload balancing across prompts. "we would consider using the KarmarkarâKarp bin-packing algorithm \citep{karmarkar1982efficient} to group prompts into approximately balanced batches"
- Knapsack problem: A classical optimization problem that selects items with values and weights to maximize total value under a capacity constraint. "This formulation is structurally identical to the {classical knapsack problem} \citep{pisinger1998knapsack}."
- Knapsack RL: The proposed approach that formulates exploration budget allocation across tasks as a knapsack optimization. "We refer to this approach as Knapsack RL; see \cref{fig:main_framework} for illustration."
- Majority voting: An aggregation strategy that selects the most common answer among multiple samples to improve reliability. "test-time scaling \citep{snell2024scaling, brown2024large}, which allocates additional computational resources (e.g., best-of- sampling, majority voting) to improve response quality."
- Megatron: A large-scale model-parallel training framework used for efficient training of LLMs. "training (e.g., FSDP \citep{zhao2023pytorch} and Megatron \citep{megatron-lm}) remain unchanged"
- Numba: A just-in-time compiler for Python that accelerates numerical computations. "With Numba \citep{lam2015numba} acceleration, it typically runs within 1â2 seconds."
- Policy gradient: A class of RL methods that optimize policies by taking the gradient of expected rewards with respect to policy parameters. "To optimize \cref{eq:reward_maximization}, policy gradient methods \citep{sutton1999policy} are commonly employed."
- RAFT: A training framework based on rejection sampling and variance reduction techniques. "which also investigates dynamic resource allocation but within rejection sampling and RAFT \citep{dong2023raft} frameworks, focusing on variance reduction."
- REINFORCE: A classic Monte Carlo policy gradient algorithm for estimating gradients from sampled returns. "Among these, REINFORCE \citep{williams1992simple}-style stochastic policy gradient methods have become standard since the work of \citep{li2024remax}."
- Relative advantage: The advantage computed relative to other samples in the same prompt group, used to update probabilities. "Technically, GRPO computes relative advantages within each response group (prompt), increasing likelihood of positive responses and decreasing likelihood of negative ones."
- Rollout: A sampled trajectory or generated response used for exploration in RL. "most RL pipelines use a small number of rollouts per prompt (e.g., 8) for exploration."
- Success rate: The probability that a model produces a correct response on a given prompt. "We define the success rate on a prompt as the probability that the model generates a correct response:"
- Test-time scaling: Increasing computational effort at inference (e.g., more samples) to improve output quality. "Our method resonates with the principle of test-time scaling \citep{snell2024scaling, brown2024large}, which allocates additional computational resources (e.g., best-of- sampling, majority voting) to improve response quality."
- vLLM: A high-throughput LLM inference engine that accelerates generation. "often leveraging efficient inference engines like vLLMs \citep{kwon2023efficient}."
- Verifiable rewards: An RL setting where rewards are determined by whether outputs can be automatically verified as correct or incorrect. "In this paper, we focus on RL with verifiable rewards \citep{lambert2024tulu}."
Collections
Sign up for free to add this paper to one or more collections.