The Flaw of Averages: Quantifying Uniformity of Performance on Benchmarks (2509.25671v1)

Abstract: Benchmarks shape scientific conclusions about model capabilities and steer model development. This creates a feedback loop: stronger benchmarks drive better models, and better models demand more discriminative benchmarks. Ensuring benchmark reliability is therefore essential for trustworthy evaluation and meaningful progress. In this work, we study benchmark reliability from a distributional perspective and introduce benchmark harmony, which measures how uniformly a model's performance is distributed across the subdomains of a benchmark. We posit that high harmony is a desirable benchmark property, indicating that the aggregate metric reflects uniform competence across subdomains. Across 19 multiple-choice benchmarks and five model families, we map each benchmark onto a mean-variance plane of harmony computed across models, where high mean and low variance signal more reliable evaluation. Our analysis shows that less harmonious benchmarks can give misleading results, since overall accuracy may be disproportionately influenced by specific subdomains. For instance, ARC-Easy is overwhelmed by questions on Biological Concepts, overshadowing other critical subdomains such as Geography, Physics, Chemistry, and Environmental Science. By recommending that harmony should be reported alongside accuracy, we reframe evaluation from simple performance averages to a more robust, distributionally reliable measurement of performance.

• The paper's main contribution is the introduction of Harmony, an entropy-based metric assessing uniform performance across benchmark subdomains.
• It employs spectral clustering with predictive similarity based on Kullback-Leibler divergence to partition benchmarks into semantic clusters.
• Findings show that higher Harmony correlates with reliable evaluations and reveal the impact of model architecture and training budgets on performance consistency.

Quantifying Uniformity of Performance on Benchmarks

The paper "The Flaw of Averages: Quantifying Uniformity of Performance on Benchmarks" explores how benchmarks are utilized to evaluate LLM capabilities and proposes a novel metric, called Harmony, to measure uniform performance across subdomains of a benchmark. This paper proposes that high Harmony is indicative of a reliable benchmark because it suggests that the benchmark reflects uniform competence across its various subdomains.

Introduction to Harmony in Benchmarks

Benchmarks are pivotal in determining the capability of LLMs and, consequently, guide the design and development of new models. Effective benchmarks should not only measure aggregate performance but also ensure that such performance is uniformly distributed across various subdomains or skills. Discrepancies in this uniformity may result in skewed perceptions of a model's competence, potentially allowing specialization in a particular subdomain to obscure weaknesses elsewhere.

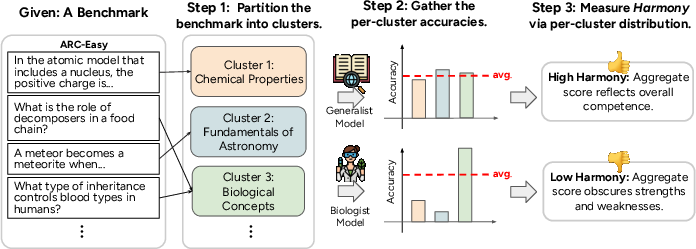
Figure 1: Pipeline of evaluating Harmony for a given benchmark. Performance is partitioned across subdomains to calculate Harmony.

To address this issue, the paper introduces the concept of Harmony, which utilizes an entropy-based metric to quantify the uniformity of performance distribution. Here, benchmarks are examined by partitioning into semantic clusters, collecting performance data for each cluster, and computing the Harmony, which denotes how evenly performance is distributed across subdomains.

Methodology and Implementation

Benchmark Harmony

Harmony is defined as the normalized Shannon entropy of performance distribution across subdomains of a benchmark. The partitioning of benchmarks into clusters is achieved via spectral clustering, grounded in a similarity function termed as predictive similarity. This function analyzes semantic similarities between data points based on Kullback-Leibler divergence across predictive distributions from LLMs.

Semantic Partition Methods

Predictive similarity serves as a robust method to discern semantic similarities by considering both the input representations and model-specific predictive outputs. Spectral clustering then leverages these similarity scores to define clusters representing specific subdomains or skills within a benchmark.

Validation

To validate the effectiveness of the proposed partitioning method, the paper introduces RedundantQA—a synthetic benchmark engineered to provide a clear, semantically structured dataset. The benchmarks CAMEO, AQUA-RAT, and MMLU were analyzed for their Harmony by evaluating different model families to assess the reliability of benchmark evaluations.

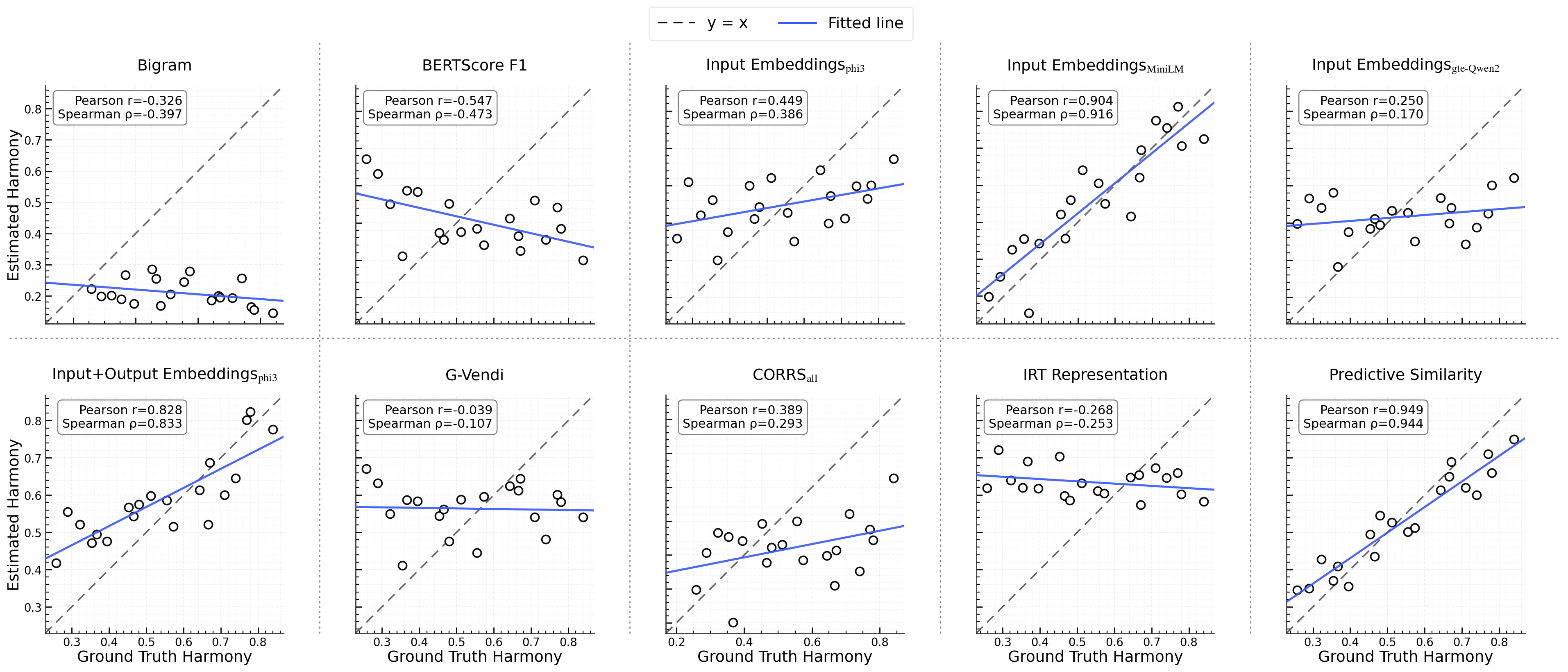
Figure 2: Validation of partition induction method on MMLU showing correlation between ground truth and estimated Harmony.

Results and Analyses

Harmony in Benchmarks

The paper places several standard benchmarks on a mean-variance plane of Harmony to assess their reliability. Benchmarks with higher Harmony (lower mean and variance) indicate more consistent evaluations, reliably reflecting model competencies across subdomains.

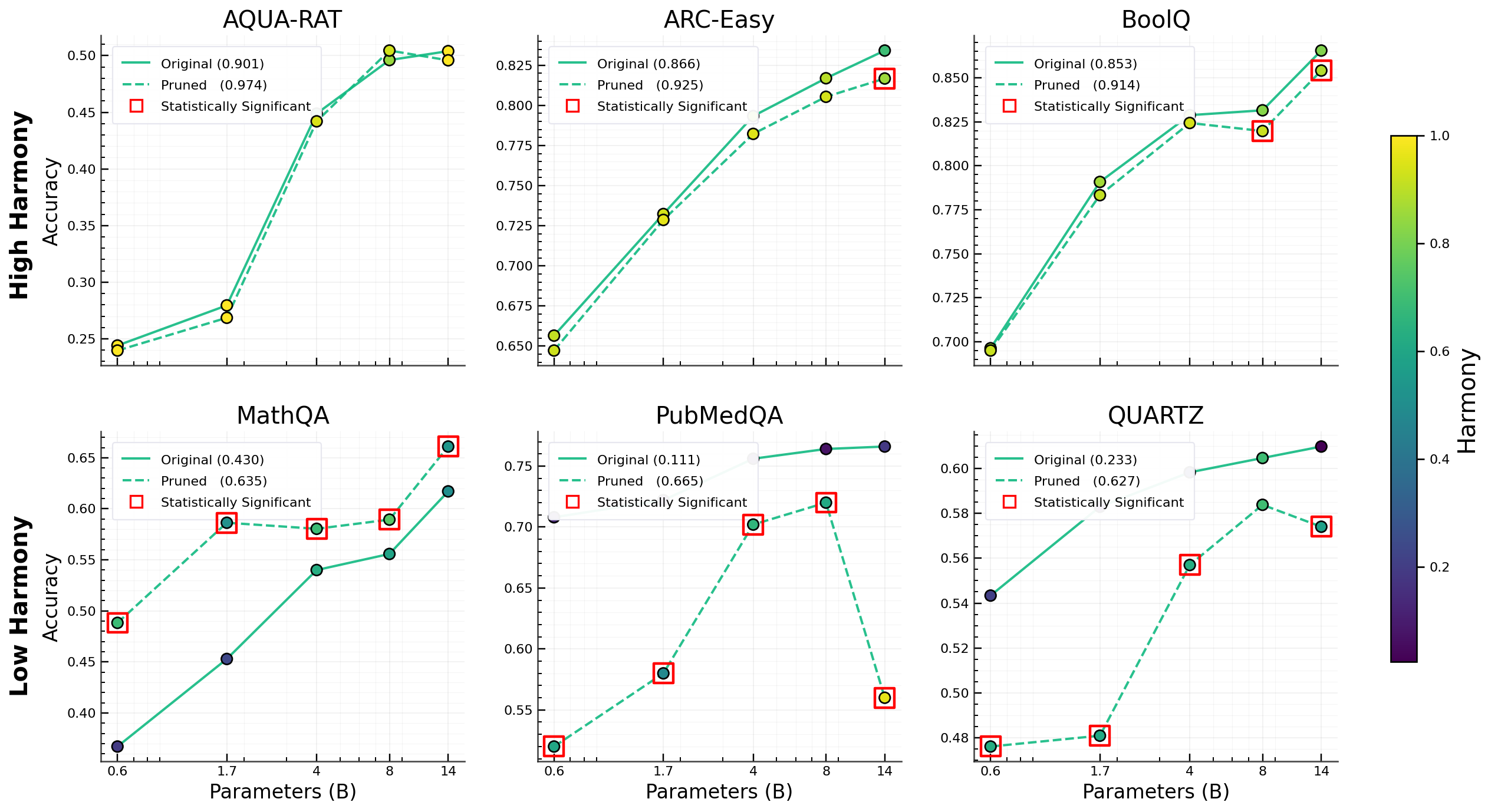
Figure 3: Balancing benchmarks via pruning to achieve stable aggregate metrics and improved Harmony.

Model-Specific Observations

The paper finds that Harmony varies not only by benchmark but by model family as well. Increasing model size and training budget could improve Harmony, but these effects are contingent on specific architectures and datasets, revealing the complexity inherent in truly assessing uniform competence.

Implications and Future Work

The introduction of Harmony represents a pivotal shift from relying solely on aggregate performance metrics to evaluations that also consider performance distribution across subdomains. Such a metric is crucial for realistic and robust evaluations of LLM capabilities.

Future research directions may involve refining the computation of Harmony through improved partitioning techniques and extending its application beyond LLMs to other domains within AI. Furthermore, continued exploration into the relationship between model architecture, training strategies, and Harmony could uncover deeper insights into model competence and evaluation.

In conclusion, the paper's contributions underscore the critical need for nuanced benchmark evaluations that offer a comprehensive understanding of a model's capabilities, thereby steering the development of stronger, more balanced models.