Signal and Noise: A Framework for Reducing Uncertainty in Language Model Evaluation (2508.13144v1)

Abstract: Developing LLMs is expensive and involves making decisions with small experiments, typically by evaluating on large, multi-task evaluation suites. In this work, we analyze specific properties which make a benchmark more reliable for such decisions, and interventions to design higher-quality evaluation benchmarks. We introduce two key metrics that show differences in current benchmarks: signal, a benchmark's ability to separate better models from worse models, and noise, a benchmark's sensitivity to random variability between training steps. We demonstrate that benchmarks with a better signal-to-noise ratio are more reliable when making decisions at small scale, and those with less noise have lower scaling law prediction error. These results suggest that improving signal or noise will lead to more useful benchmarks, so we introduce three interventions designed to directly affect signal or noise. For example, we propose that switching to a metric that has better signal and noise (e.g., perplexity rather than accuracy) leads to better reliability and improved scaling law error. We also find that filtering noisy subtasks, to improve an aggregate signal-to-noise ratio, leads to more reliable multi-task evaluations. We also find that averaging the output of a model's intermediate checkpoints to reduce noise leads to consistent improvements. We conclude by recommending that those creating new benchmarks, or selecting which existing benchmarks to use, aim for high signal and low noise. We use 30 benchmarks for these experiments, and 375 open-weight LLMs from 60M to 32B parameters, resulting in a new, publicly available dataset of 900K evaluation benchmark results, totaling 200M instances.

• The paper introduces a framework quantifying signal and noise to predict decision accuracy and scaling law error in language model evaluation.
• It employs extensive empirical analysis across 30 benchmarks and 465 models, demonstrating strong correlations with SNR achieving R=0.791 for decision accuracy.
• The study proposes practical interventions like noisy subtask filtering, checkpoint averaging, and metric reformulation to enhance benchmark reliability.

Signal and Noise: A Framework for Reducing Uncertainty in LLM Evaluation

Introduction

This paper presents a rigorous framework for quantifying and reducing uncertainty in LLM evaluation by introducing two key metrics: signal and noise. Signal is defined as a benchmark’s ability to distinguish between better and worse models, while noise captures the sensitivity of benchmark scores to random variability during training. The authors demonstrate that benchmarks with higher signal and lower noise yield more reliable predictions when extrapolating from small-scale experiments to large-scale model behavior. The work is grounded in extensive empirical analysis across 30 benchmarks and 465 models, spanning 60M to 32B parameters, and introduces practical interventions to improve benchmark reliability.

Formalization of Signal and Noise

The authors formalize two common experimental settings in LLM development: (1) decision accuracy, which measures the agreement in model ranking between small and large models, and (2) scaling law prediction error, which quantifies the error in predicting large model performance from scaling laws fit to small models. Signal is operationalized as the relative dispersion of model scores on a benchmark, while noise is measured as the relative standard deviation of scores across the final $n$ training checkpoints.

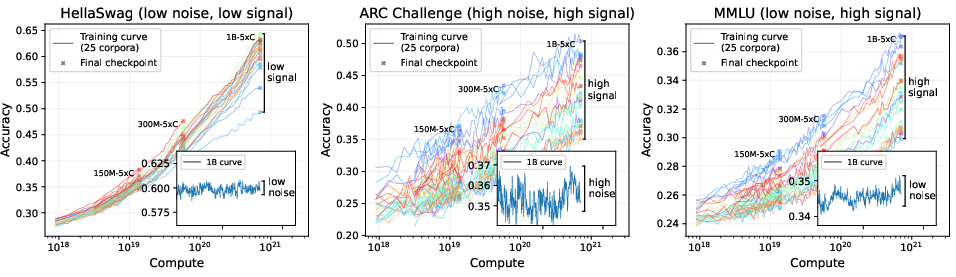
Figure 1: Training curves for 25 pretraining corpora on three benchmarks, illustrating the relationship between signal, noise, and decision accuracy across model scales.

The signal-to-noise ratio (SNR) is introduced as a composite metric, defined as the ratio of signal to noise, and shown to be highly predictive of both decision accuracy and scaling law prediction error.

Figure 2: Correlation between signal, noise, and SNR with decision accuracy; SNR is strongly predictive of decision accuracy, while signal or noise alone are not.

Empirical Findings

Signal Predicts Decision Accuracy

Benchmarks with higher SNR at small scales exhibit higher decision accuracy, meaning that the ranking of small models is more likely to generalize to large models. The authors report a strong correlation ($R=0.791$, $R^2=0.626$) between SNR and decision accuracy across the OLMES benchmarks.

Noise Predicts Scaling Law Error

Noise in the target model’s final checkpoints is shown to correlate with scaling law prediction error ($R=0.653$, $R^2=0.426$). Benchmarks with lower noise yield more reliable scaling law predictions, and the noise acts as a lower bound on achievable prediction error.

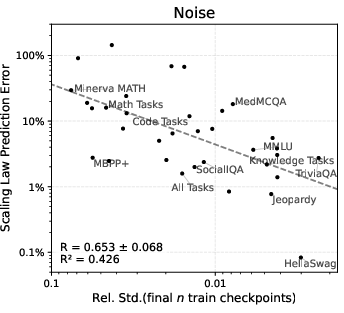
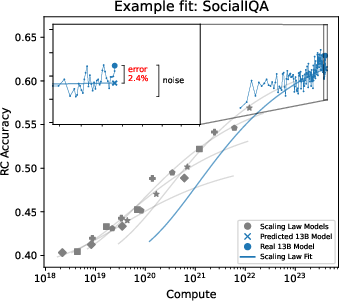
Figure 3: Correlation between noise and scaling law prediction error; lower noise benchmarks yield lower prediction error.

Interventions to Improve Benchmark Reliability

The authors propose and empirically validate three interventions to improve SNR and thus benchmark reliability:

1. Filtering Noisy Subtasks

By ranking subtasks within a benchmark by SNR and selecting high-SNR subsets, decision accuracy and scaling law prediction error are improved, even when the subset contains fewer instances than the full benchmark.

Figure 4: Subset selection by SNR for MMLU and AutoBencher; high-SNR subsets yield higher decision accuracy and lower noise.

2. Averaging Checkpoint Scores

Averaging scores across multiple final training checkpoints reduces noise and consistently improves both decision accuracy and scaling law prediction error. This is effective for both small and large models, and also improves early-stopping predictions.

Figure 5: Averaging checkpoint-to-checkpoint noise improves decision accuracy for early-stopping across multiple benchmarks.

3. Metric Reformulation: Bits-per-Byte

Switching from discontinuous metrics (e.g., accuracy, exact match) to continuous metrics such as bits-per-byte (BPB) increases SNR, reduces scaling law prediction error, and improves decision accuracy for the majority of benchmarks, especially for generative tasks.

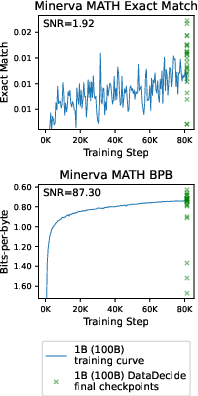
Figure 6: BPB metric yields higher SNR, lower scaling law error, and higher decision accuracy compared to primary metrics across benchmarks.

Scaling and Sample Size Analysis

The paper demonstrates that increasing benchmark size yields diminishing returns in SNR beyond a certain point, and that small, high-quality benchmarks can outperform larger, noisier ones. SNR is also shown to be a useful indicator of benchmark utility at larger model scales (up to 32B parameters), with some benchmarks saturating in SNR as model size increases.

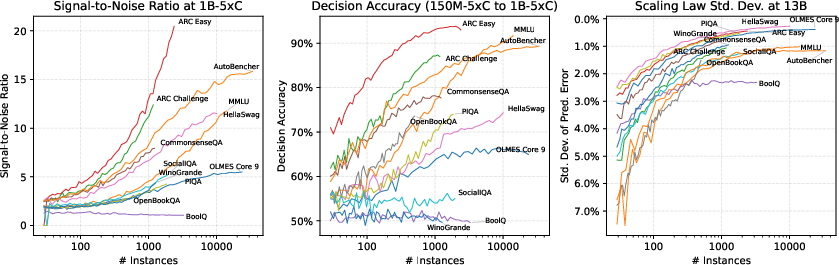
Figure 7: Increasing sample size does not guarantee improved signal; small, high-SNR benchmarks can outperform larger ones.

Practical Implications

The framework provides actionable guidance for benchmark developers and practitioners:

• Benchmark selection: Prefer benchmarks with high SNR for development decisions and scaling law extrapolation.
• Benchmark construction: Filter out low-SNR subtasks and consider continuous metrics to improve reliability.
• Evaluation protocol: Average scores across multiple checkpoints to reduce noise.
• Scaling law fitting: Use benchmarks with low noise for more accurate extrapolation.

The authors release a large, open dataset of 900K evaluation results to facilitate further research.

Theoretical Implications and Future Directions

The work establishes SNR as a principled, computationally efficient proxy for benchmark utility in LLM development. It highlights the limitations of relying solely on benchmark size or traditional metrics, and suggests that SNR should be a standard criterion in benchmark design and selection. Future research may extend the framework to other sources of modeling noise, emergent capabilities, and evaluation configurations.

Conclusion

This paper provides a robust framework for quantifying and reducing uncertainty in LLM evaluation via signal and noise metrics. The empirical results demonstrate that SNR is a reliable predictor of benchmark utility for both decision accuracy and scaling law extrapolation. The proposed interventions—subtask filtering, checkpoint averaging, and metric reformulation—offer practical methods to improve benchmark reliability. The findings have significant implications for benchmark development, model selection, and evaluation protocols in large-scale LLM research.