Advantage Weighted Matching: Aligning RL with Pretraining in Diffusion Models (2509.25050v1)

Abstract: Reinforcement Learning (RL) has emerged as a central paradigm for advancing LLMs, where pre-training and RL post-training share the same log-likelihood formulation. In contrast, recent RL approaches for diffusion models, most notably Denoising Diffusion Policy Optimization (DDPO), optimize an objective different from the pretraining objectives--score/flow matching loss. In this work, we establish a novel theoretical analysis: DDPO is an implicit form of score/flow matching with noisy targets, which increases variance and slows convergence. Building on this analysis, we introduce \textbf{Advantage Weighted Matching (AWM)}, a policy-gradient method for diffusion. It uses the same score/flow-matching loss as pretraining to obtain a lower-variance objective and reweights each sample by its advantage. In effect, AWM raises the influence of high-reward samples and suppresses low-reward ones while keeping the modeling objective identical to pretraining. This unifies pretraining and RL conceptually and practically, is consistent with policy-gradient theory, reduces variance, and yields faster convergence. This simple yet effective design yields substantial benefits: on GenEval, OCR, and PickScore benchmarks, AWM delivers up to a $24\times$ speedup over Flow-GRPO (which builds on DDPO), when applied to Stable Diffusion 3.5 Medium and FLUX, without compromising generation quality. Code is available at https://github.com/scxue/advantage_weighted_matching.

• The paper introduces AWM, a policy-gradient method that reweights the score matching loss with reward advantages to reduce variance in RL training.
• It demonstrates significant improvements, including up to 8× faster convergence on GenEval and 24× reduced compute for OCR tasks, without sacrificing quality.
• The study bridges RL post-training and pretraining by theoretically linking DDPO with noisy score matching, offering practical efficiency in diffusion models.

Advantage Weighted Matching: Unifying RL and Pretraining Objectives in Diffusion Models

Introduction

The paper "Advantage Weighted Matching: Aligning RL with Pretraining in Diffusion Models" (2509.25050) presents a rigorous theoretical and empirical analysis of reinforcement learning (RL) post-training for diffusion models, identifying a key source of inefficiency in existing approaches and introducing a new method, Advantage Weighted Matching (AWM), that achieves substantial improvements in training speed and conceptual alignment with pretraining. The work establishes that the widely adopted Denoising Diffusion Policy Optimization (DDPO) framework is an implicit form of denoising score matching (DSM) with noisy targets, which increases variance and slows convergence. AWM is proposed as a policy-gradient method that directly incorporates reward signals into the score/flow matching loss, reweighting samples by their advantage, and thereby unifying RL post-training and pretraining objectives.

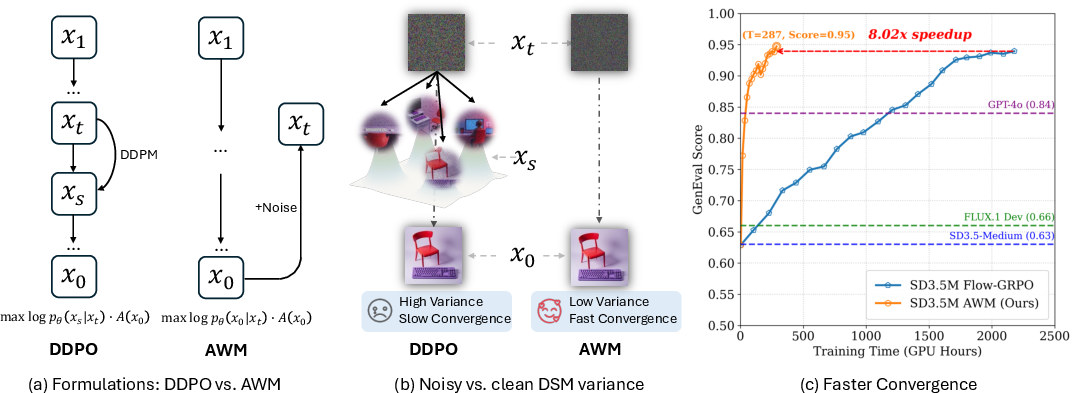
Figure 1: AWM reduces variance and speeds up RL for diffusion. (a) DDPO optimizes per-step Gaussian likelihood on $x_{t-1}$, while AWM applies reward-weighted score/flow matching on $x_0$. (b) DDPO's noisy conditioning increases variance. (c) AWM achieves up to $8\times$ faster convergence on GenEval.

Theoretical Analysis: DDPO as Noisy Score Matching

The paper provides a formal equivalence between DDPO and DSM with noisy data. DDPO, which frames the reverse-time denoising process as a multi-step Markov Decision Process (MDP), optimizes per-step Gaussian likelihoods conditioned on noisy intermediate states. The authors prove that this is equivalent to minimizing DSM with noisy data, regardless of score or velocity parameterization. While both DDPO and standard pretraining (which uses clean data) share the same population minimizer, conditioning on noisy data strictly increases the variance of the score function estimator. This variance inflation is quantified analytically and validated empirically.

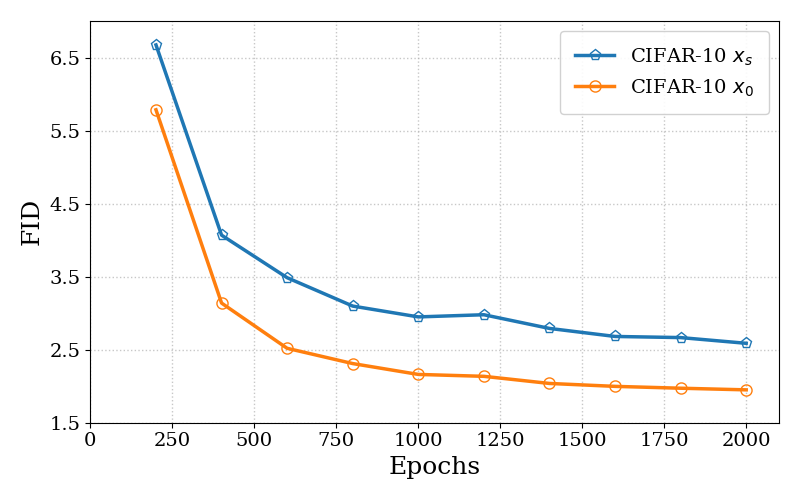
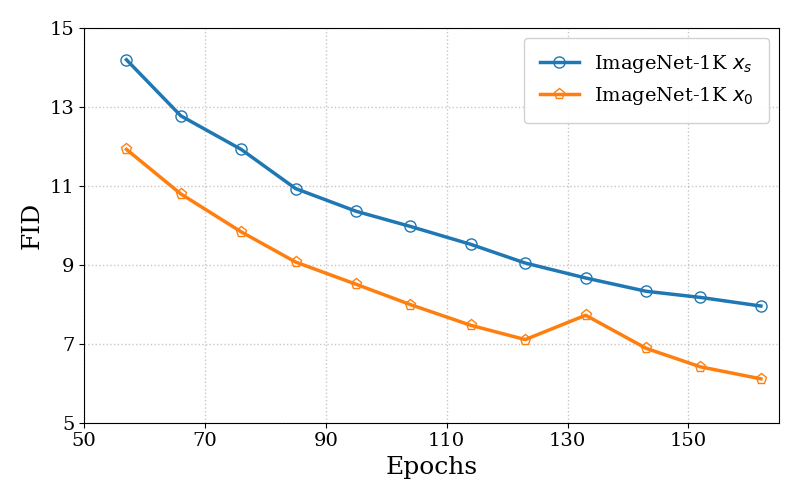
Figure 2: FID on CIFAR-10. Noisy conditioning (DDPO proxy) yields consistently worse FID and slower convergence than clean-data objectives.

The increased variance in DDPO's objective leads to slower stochastic optimization, as demonstrated in controlled pretraining experiments on CIFAR-10 and ImageNet-64. The noisy-DSM objective converges more slowly and achieves inferior FID scores under identical settings, confirming the theoretical predictions.

Advantage Weighted Matching: Methodology and Implementation

AWM is introduced to address the variance amplification in DDPO by evaluating the score/flow matching loss on clean data and reweighting each sample by its advantage. This approach preserves the original pretraining objective and amplifies the influence of high-reward samples, suppressing low-reward ones. AWM decouples training from sampling, allowing the use of arbitrary samplers (ODE/SDE) and noise levels, and restores conceptual symmetry between diffusion models and LLMs, where both pretraining and RL post-training optimize the same objective with reward-dependent weighting.

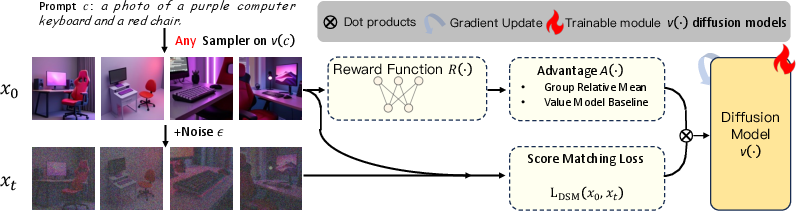
Figure 3: AWM pipeline. For each prompt, a group of sequences is sampled, rewards and advantages are computed, and the policy is updated via advantage-weighted score matching.

Pseudocode

The core AWM training loop is as follows:

for i in range(num_training_steps): samples = sampler(model, prompt) reward = reward_fn(samples) advantage = cal_adv(reward, prompt) noise = randn_like(samples) timesteps = get_timesteps(samples) noisy_samples = fwd_diffusion(samples, noise, timesteps) velocity_pred = model(noisy_samples, timesteps, prompt) velocity_ref = ref_model(noisy_samples, timesteps, prompt) # optional KL log_p = -((velocity_pred - (noise-samples))**2).mean() ratio = torch.exp(log_p - log_p.detach()) policy_loss = -advantage * ratio kl_loss = weight(timesteps)*((velocity_pred - velocity_ref)**2).mean() loss = policy_loss + beta * kl_loss

Key implementation details:

• Advantage Calculation: Group-relative mean is used for stable advantage estimation.
• KL Regularization: A velocity-space KL term stabilizes updates.
• Timesteps and Sampler: Training and sampling timesteps are decoupled; any sampler can be used.
• Data Reuse: On-policy and one-step off-policy updates yield similar performance, enabling efficient batch reuse.

Empirical Results

AWM delivers dramatic improvements in training efficiency across multiple benchmarks and model backbones, including Stable Diffusion 3.5 Medium (SD3.5M) and FLUX. On GenEval, AWM matches Flow-GRPO's overall score (0.95) with an 8.02× speed-up in GPU hours. For OCR and PickScore tasks, AWM achieves up to 24× faster convergence without compromising generation quality.

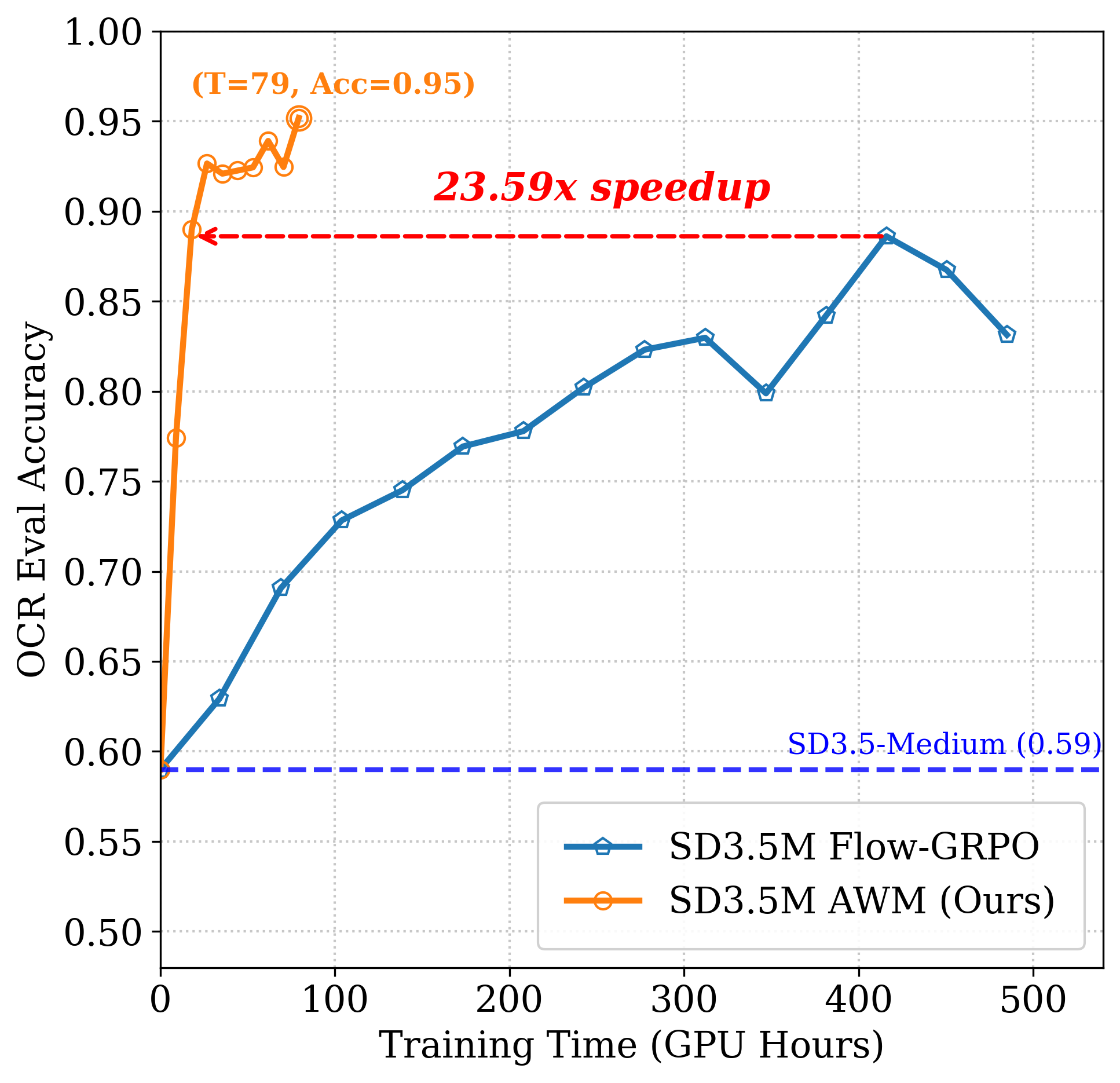
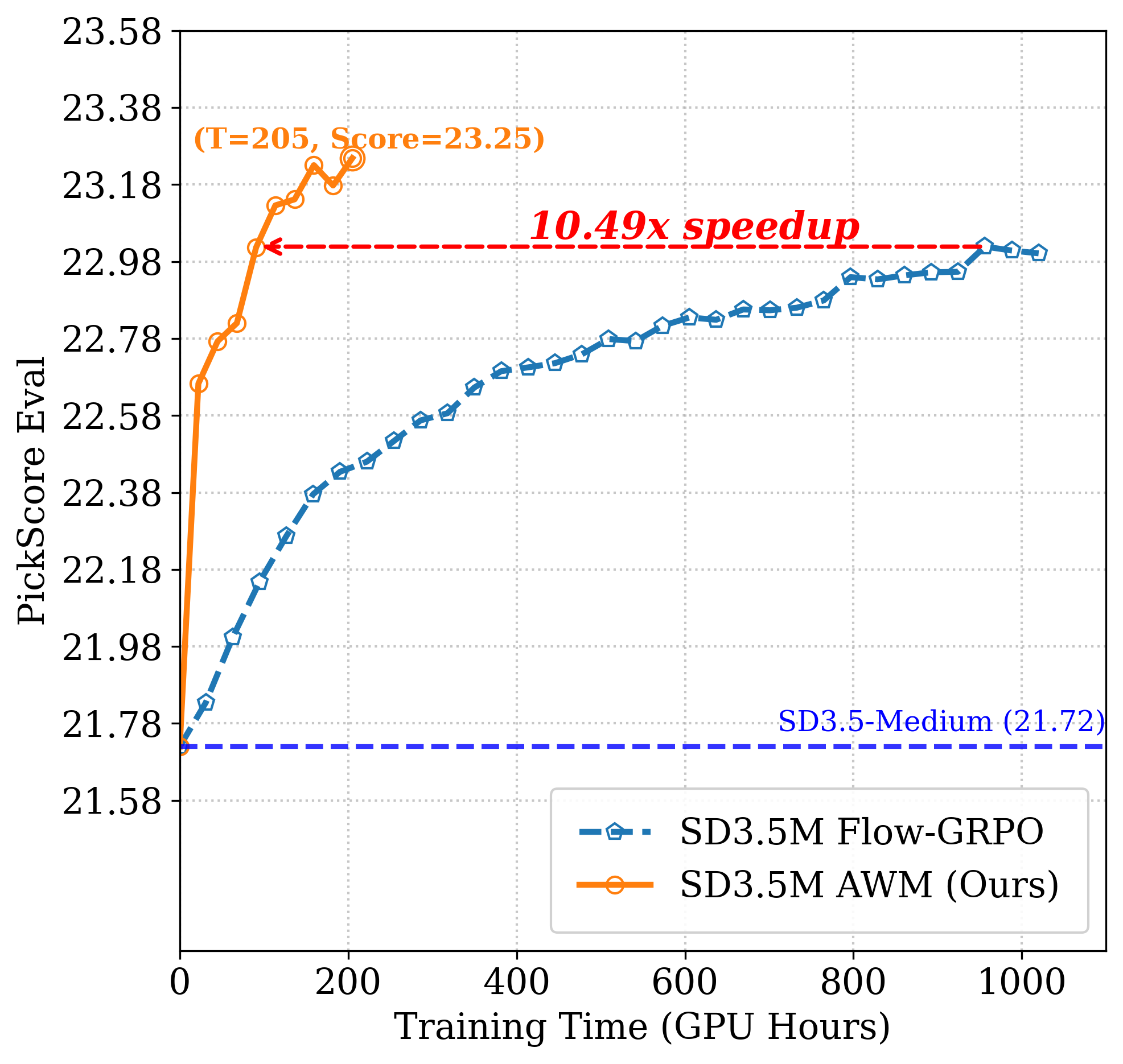
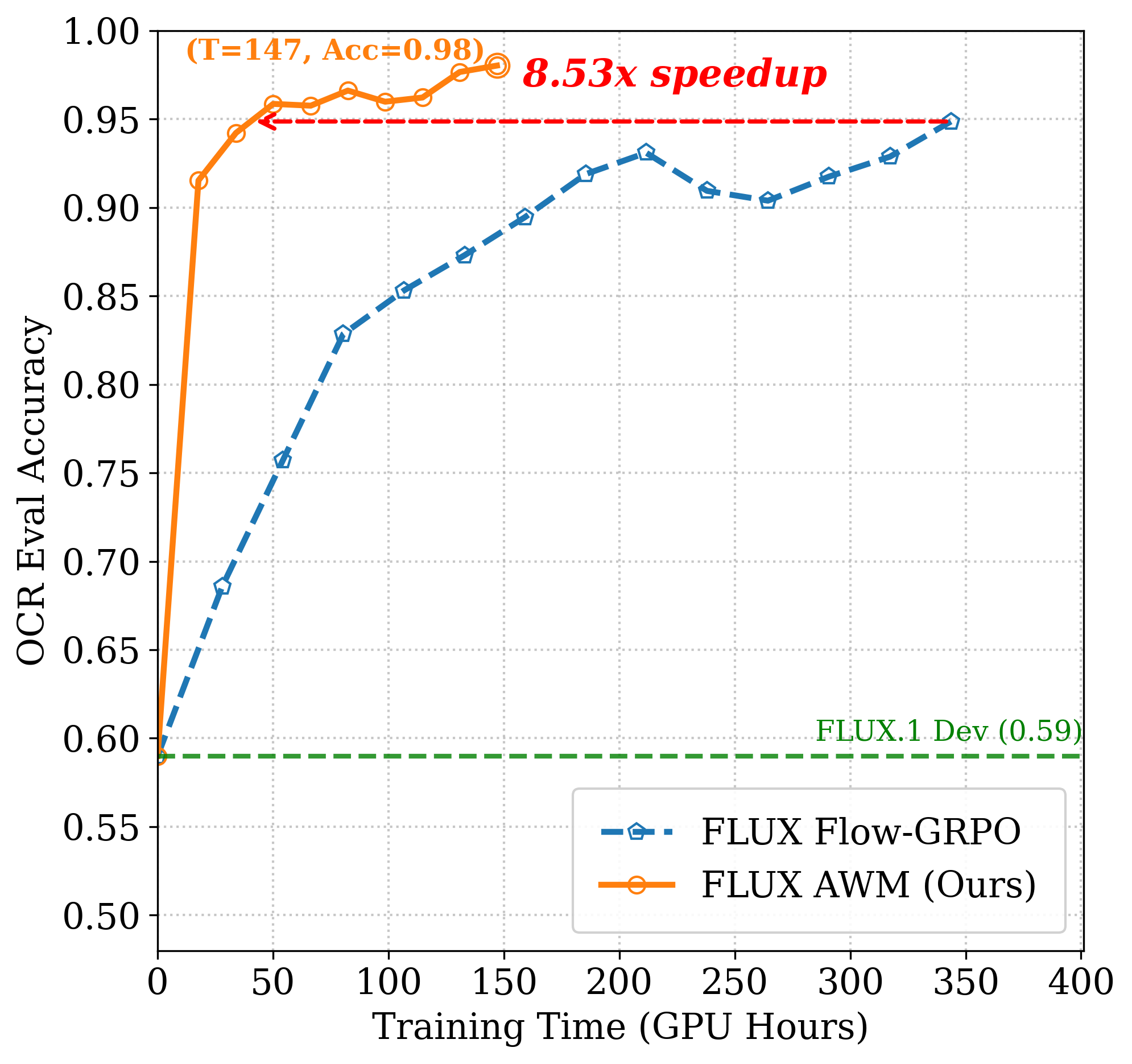
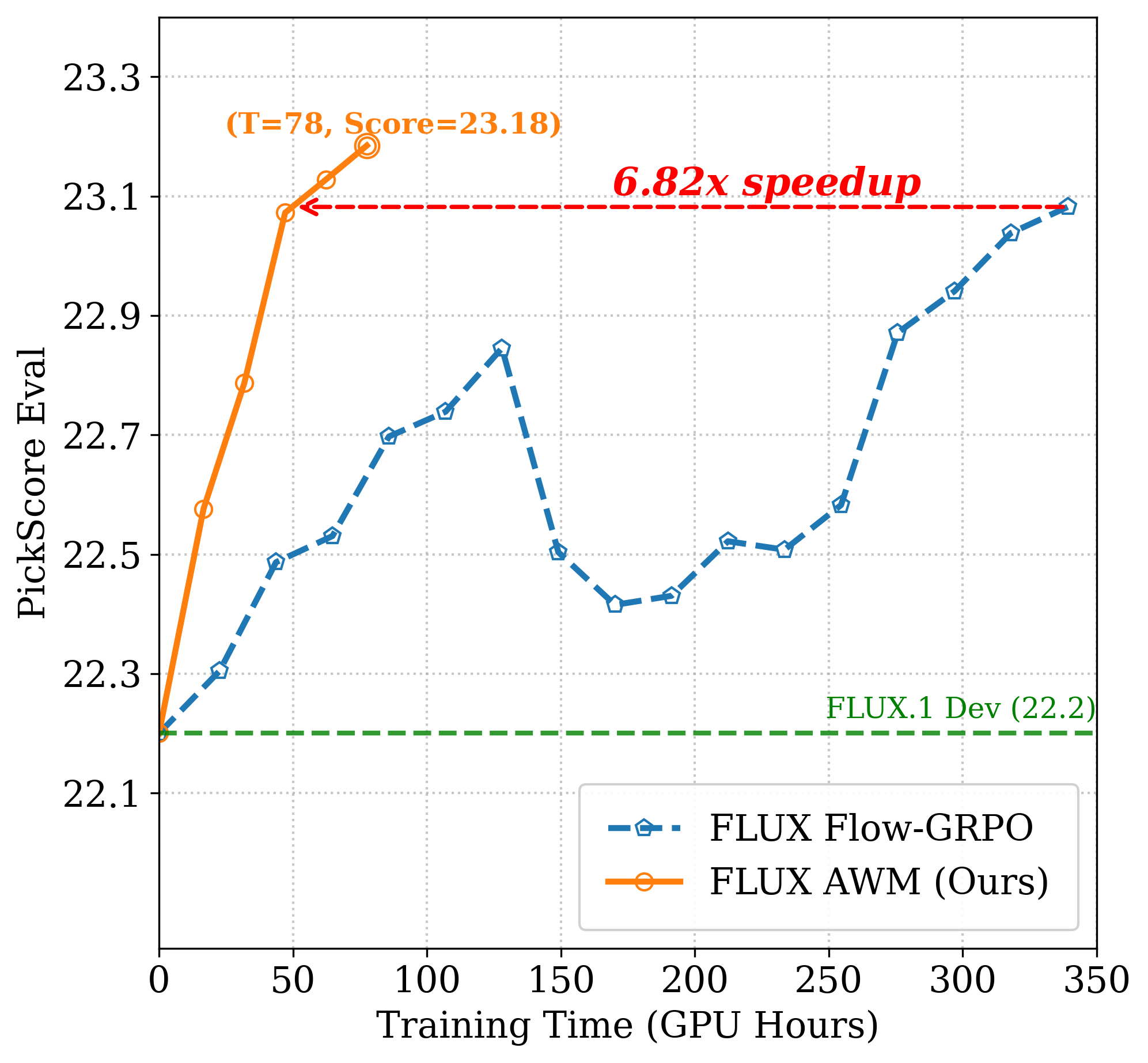
Figure 4: SD3.5M OCR. AWM achieves target accuracy with 23.6× less compute than Flow-GRPO.

Figure 5: Visual comparison before and after AWM training. AWM improves compositional and text rendering fidelity on GenEval and OCR prompts.

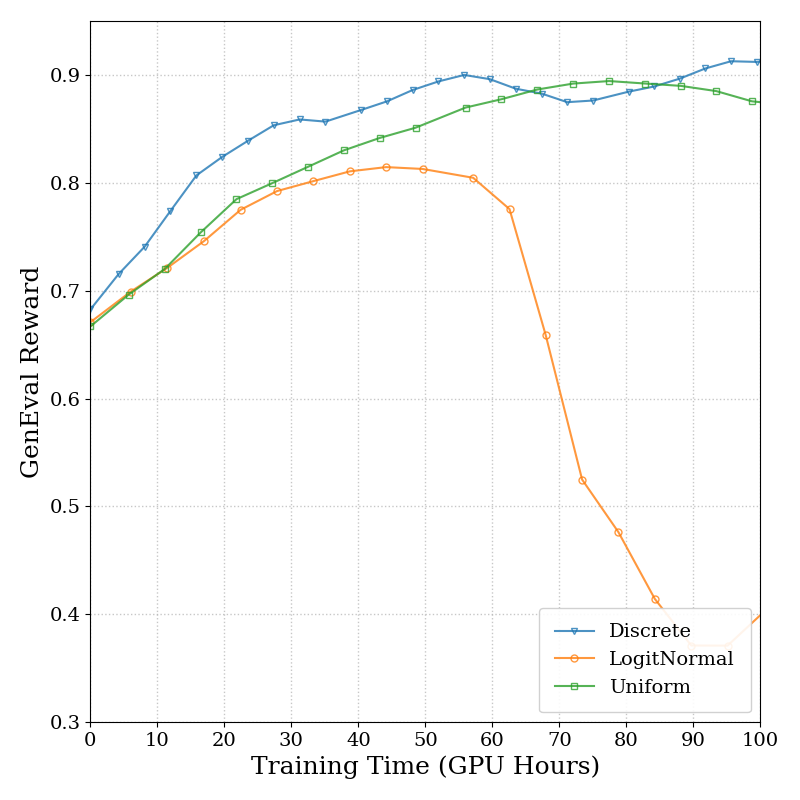
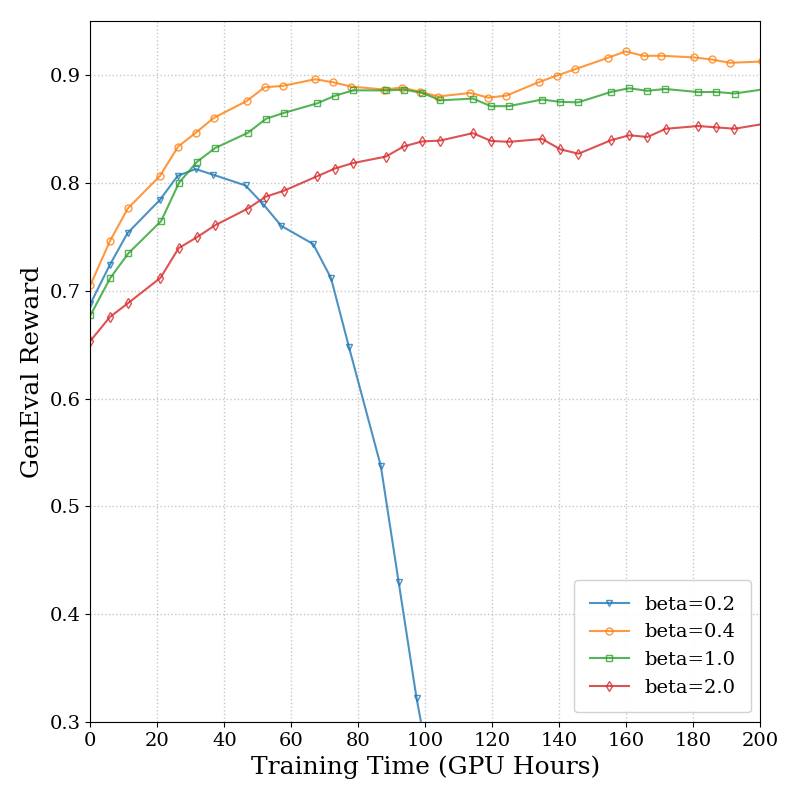
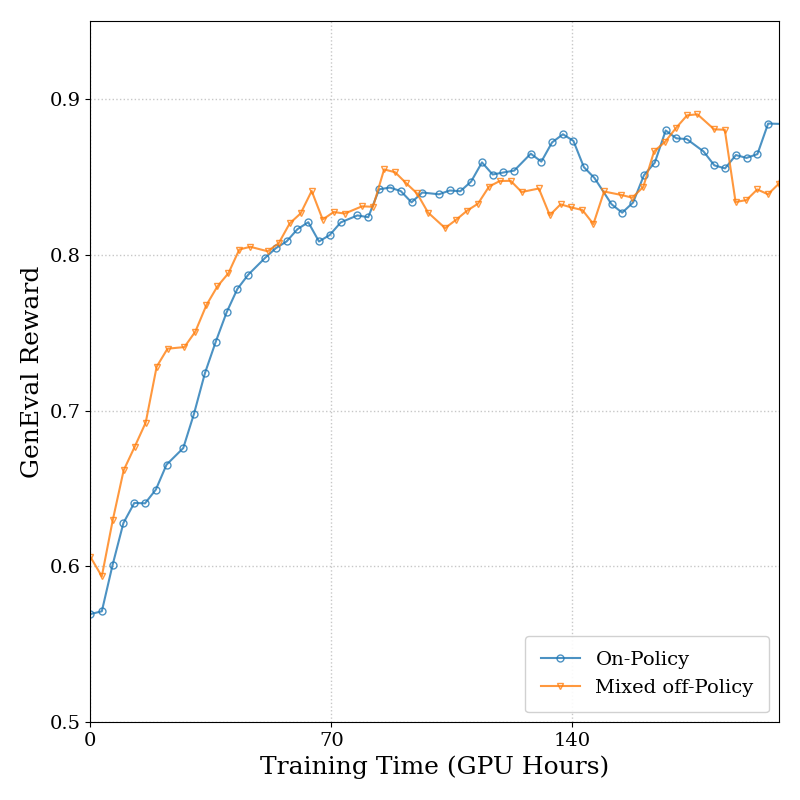
Figure 6: SD3.5M Time. Ablation on timestep sampling, KL strength, and data reuse shows robust performance and stable convergence.

AWM consistently outperforms DDPO-based methods in terms of wall-clock efficiency, with no degradation in sample quality. Visualizations confirm improved adherence to compositional and text rendering constraints after AWM training.

Ablation Studies

Ablations on timestep sampling distribution, KL regularization strength, and data reuse strategies demonstrate that AWM is robust to hyperparameter choices. Discrete and uniform timestep sampling yield similar results, while KL regularization in the range $[0.4, 1.0]$ is optimal for stability and speed. Mixed on-policy/off-policy updates enable efficient data reuse without loss of performance.

Practical and Theoretical Implications

AWM unifies RL post-training and pretraining for diffusion models under a single, policy-gradient–consistent objective, mirroring the alignment found in LLMs. This conceptual symmetry simplifies the training pipeline, reduces the need for custom sampling strategies, and enables the use of advanced ODE/SDE samplers. The variance reduction achieved by AWM translates directly into faster convergence and lower computational cost, making RL post-training practical for large-scale diffusion models.

Theoretically, the work clarifies the relationship between DDPO and score matching, quantifies the impact of noisy conditioning, and provides a foundation for future RL algorithms that maintain alignment with pretraining objectives. Practically, AWM enables efficient reward-driven fine-tuning of diffusion models for tasks requiring compositionality, text rendering, and human preference alignment.

Future Directions

Potential future developments include:

• Extending AWM to support deeper off-policy data reuse and more sophisticated advantage estimation.
• Leveraging advanced ODE/SDE samplers for further improvements in sample quality and speed.
• Applying AWM to other generative domains (e.g., video, 3D synthesis) and reward functions.
• Investigating the integration of AWM with step-distilled models for accelerated sampling.

Conclusion

The paper establishes a rigorous theoretical connection between DDPO and score matching, identifies variance amplification as a key bottleneck, and introduces AWM as a principled, efficient alternative. AWM achieves up to $24\times$ faster convergence than Flow-GRPO on SD3.5M and FLUX, with no loss in generation quality. The method unifies RL post-training and pretraining for diffusion models, providing both practical efficiency and conceptual clarity for future research and deployment.