A Unifying Framework for Parallelizing Sequential Models with Linear Dynamical Systems (2509.21716v1)

Abstract: Harnessing parallelism in seemingly sequential models is a central challenge for modern machine learning. Several approaches have been proposed for evaluating sequential processes in parallel using fixed-point methods, like Newton, Picard, and Jacobi iterations. In this work, we show that these methods can be understood within a common framework based on linear dynamical systems (LDSs), where different iteration schemes arise naturally as approximate linearizations of a nonlinear recursion. This unifying view highlights shared principles behind these techniques and clarifies when particular fixed-point methods are most likely to be effective. By bridging diverse algorithms through the language of LDSs, our framework provides a clearer theoretical foundation for parallelizing sequential models and points toward new opportunities for efficient and scalable computation.

• The paper presents a framework that recasts diverse fixed-point methods (Newton, quasi-Newton, Picard, Jacobi) as iterative LDS evaluations to parallelize sequential models.
• It demonstrates reducing sequential runtime from O(T) to O(log T) through parallel scan algorithms and provides empirical case studies on convergence and resource trade-offs.
• The work offers practical guidelines for selecting methods based on convergence speed, memory use, and hardware constraints in RNNs, diffusion models, and other sequence tasks.

Unifying Parallel Fixed-Point Methods for Sequential Models via Linear Dynamical Systems

This paper presents a rigorous framework that unifies diverse approaches to parallelizing sequential machine learning models through the lens of Linear Dynamical Systems (LDSs). It demonstrates that fixed-point methods—including Newton, quasi-Newton, Picard, and Jacobi iterations—can all be cast as iterative LDS evaluations, thereby facilitating parallelization of nonlinear recursive processes that traditionally appear inherently sequential. The authors provide precise mathematical characterization, algorithmic details, and empirical guidance regarding method selection with respect to problem structure and hardware constraints.

Fixed-Point Iterations as Parallel Linear Dynamical Systems

The core technical contribution is the proof that fixed-point solvers for nonlinear recursions, $x_{t+1} = f_{t+1}(x_t)$, can be transformed into iterative application of LDSs, with the transition matrix $A_{t+1}$ approximating the Jacobian $\frac{\partial f_{t+1}}{\partial x_t}$. By executing these LDSs with a parallel scan algorithm, practitioners can reduce evaluation time from $\mathcal{O}(T)$ to $\mathcal{O}(\log T)$ on appropriate parallel hardware.

• Newton Iterations use the full Jacobian for maximal convergence per iteration, but incur $\mathcal{O}(T D^2)$ memory and $\mathcal{O}(T D^3)$ compute per step.
• Quasi-Newton Iterations (e.g., diagonal Jacobian) lower computational cost to $\mathcal{O}(T D)$ but require more iterations.
• Picard Iterations set $A = I_D$, yielding minimal memory footprint and computational cost.
• Jacobi Iterations set $A = 0$, which is only suitable for non-Markovian recurrences.

An important theoretical result is global convergence for all these methods within $T$ iterations for any Markovian sequence, irrespective of the linearization quality.

Figure 1: Iterative formation of "parallel chords" in Newton's method underlines the geometric intuition behind linearizing nonlinear recursive updates at each fixed-point iteration.

Method Selection: Empirical Case Studies

The framework is concretized via three canonical experiments, each assessing convergence properties and resource utilization trade-offs.

Case 1: Group Word Problem

Linear recursions with input-dependent, non-diagonal transition matrices (e.g., permutation matrices for $S_5$ group word problem) demonstrate that Newton iterations converge in a single iteration, whereas Quasi-Newton and Picard require up to $T$ iterations due to suboptimal Jacobian approximations. Wall-clock time confirms that full Newton is preferable when memory allows.

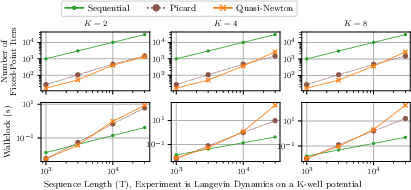
Figure 2: In a similar setting as Figure 2well (Langevin), fast convergence is observed for Newton iterations; alternative methods scale poorly with problem size.

Case 2: RNNs with Nonlinear Dynamics

Nonlinear GRU models with full coupling between latent dimensions are poorly approximated by $I_D$ (Picard) or diagonal Jacobians (Quasi-Newton), except possibly for special network initializations. First-order methods, especially Quasi-Newton, balance convergence speed and resource usage, outperforming Picard in both iterations and wall-clock time for typical RNN use cases.

Case 3: Langevin Dynamics and Diffusion Models

When the Jacobian is close to the identity—as in discretized Langevin diffusion with small step size—Picard iterations are highly efficient, rapidly converging with minimal hardware burden. This phenomenon generalizes to other scenarios with weak coupling or nearly identity dynamics functions.

Implementation and Deployment Guidance

Selecting the optimal fixed-point strategy involves balancing convergence per iteration, per-iteration resource intensity, and overall wall-clock time.

• Newton: Use for small-$D$ and short-$T$, or when low-iteration count is critical and hardware permits full Jacobian evaluation.
• Quasi-Newton: Preferred in high-dimensional or long sequences, especially when diagonal Jacobian suffices—a sweet spot for practical deployment.
• Picard: Optimal for nearly-linear, weakly-coupled dynamics or when extreme memory constraints exist.
• Jacobi: Only for specialized non-Markovian architectures (e.g., deeply skip-connected networks).

Numerical stability must be actively monitored, especially for LDS matrices with spectral norm near unity. Chunking and hybrid fixed-point/scan strategies can further alleviate hardware bottlenecks.

Theoretical and Practical Implications

The unification of parallel fixed-point methods via LDSs establishes:

• A precise mapping between linearizations of nonlinear recursions and parallel scan implementations.
• Global convergence (within sequence length $T$) for all LDS-cast fixed-point methods in Markovian settings.
• Empirical guidelines for matching method to problem structure and hardware characteristics.

The framework lends itself to direct application in deep state space models, diffusion model sampling, implicit layers, MCMC, and any sequence modeling scenario requiring efficient parallel computation. Future work may focus on efficient parameterizations of structured transition matrices (e.g., block-diagonal, permutation, scaled identity), optimal chunking strategies, and integration with high-throughput hardware primitives.

Conclusion

By expressing Newton, quasi-Newton, Picard, and related solvers as iterative LDS evaluations that admit parallel scan computation, this work offers both an elegant theoretical synthesis and actionable guidance for practitioners seeking to parallelize inherently sequential machine learning processes. The authors’ case studies show that appropriate method selection—guided by Jacobian structure, memory constraints, and hardware specifics—enables significant efficiency gains in real-world deployments.

Future research directions include developing adaptive Jacobian approximations for intermediate complexity recurrences, optimizing LDS implementation on emerging hardware, and extending the framework to stochastic and probabilistic dynamical models. This unified treatment sets a foundational standard for both algorithmic analysis and design of parallel sequential model architectures.