Neural Low-Discrepancy Sequences (2510.03745v1)

Abstract: Low-discrepancy points are designed to efficiently fill the space in a uniform manner. This uniformity is highly advantageous in many problems in science and engineering, including in numerical integration, computer vision, machine perception, computer graphics, machine learning, and simulation. Whereas most previous low-discrepancy constructions rely on abstract algebra and number theory, Message-Passing Monte Carlo (MPMC) was recently introduced to exploit machine learning methods for generating point sets with lower discrepancy than previously possible. However, MPMC is limited to generating point sets and cannot be extended to low-discrepancy sequences (LDS), i.e., sequences of points in which every prefix has low discrepancy, a property essential for many applications. To address this limitation, we introduce Neural Low-Discrepancy Sequences ($NeuroLDS$), the first machine learning-based framework for generating LDS. Drawing inspiration from classical LDS, we train a neural network to map indices to points such that the resulting sequences exhibit minimal discrepancy across all prefixes. To this end, we deploy a two-stage learning process: supervised approximation of classical constructions followed by unsupervised fine-tuning to minimize prefix discrepancies. We demonstrate that $NeuroLDS$ outperforms all previous LDS constructions by a significant margin with respect to discrepancy measures. Moreover, we demonstrate the effectiveness of $NeuroLDS$ across diverse applications, including numerical integration, robot motion planning, and scientific machine learning. These results highlight the promise and broad significance of Neural Low-Discrepancy Sequences. Our code can be found at https://github.com/camail-official/neuro-lds.

• The paper presents NeuroLDS, a neural framework that generates extensible low-discrepancy sequences outperforming classical sequences in various metrics.
• The model employs a two-stage learning process with pretraining on classical sequences and fine-tuning using closed-form discrepancy loss to ensure stability and performance.
• The approach demonstrates superior convergence in quasi-Monte Carlo integration, robot motion planning, and scientific ML, marking significant practical improvements.

Neural Low-Discrepancy Sequences: Methodology and Empirical Performance

Introduction and Problem Motivation

Low-discrepancy sequences (LDS) are foundational to quasi-Monte Carlo (QMC) methods, enabling deterministic, space-filling sampling of $[0,1]^d$ that markedly improves convergence rates in high-dimensional numerical integration, Bayesian inference, computer vision, simulation, and scientific ML. While classical constructions (e.g., Sobol’, Halton, digital nets, rank-1 lattices) are based on algebraic structures, recent advances have explored ML-based optimization for minimizing discrepancy. Message-Passing Monte Carlo (MPMC), utilizing a GNN, set a new standard in low-discrepancy point set construction, but is fundamentally limited to fixed cardinality sets, lacking the essential extensibility property of true LDS.

The Neural Low-Discrepancy Sequences (NeuroLDS) framework overcomes this by introducing a neural sequence generator that matches or surpasses state-of-the-art discrepancy metrics for every prefix of the sequence, thus addressing the intrinsic challenge of extensibility.

Construction of NeuroLDS

Model Architecture

NeuroLDS defines a mapping $f_\theta: \{1, ..., N\} \rightarrow [0,1]^d$ implemented as an $L$-layer MLP with ReLU activations and a terminal sigmoid. To endow the model with the expressivity needed to mimic classic combinatorial and number-theoretic transformations, the input index $i$ undergoes $K$-band sinusoidal (Fourier-style) positional encoding, exposing multi-scale periodic structure to the neural network. This setup parallels but generalizes the classical radical-inverse and direction number expansions used in the Halton and Sobol' sequences, with the neural MLP replacing rigid arithmetical computation with learnable mappings. The resulting sequence is strictly deterministic and efficiently computable for arbitrary index $i$.

Two-Stage Learning: Pretraining and Fine-Tuning

NeuroLDS employs a two-phase optimization strategy:

• Pretraining: The MLP is first trained to regress onto a reference LDS (typically Sobol’) using MSE loss, optionally after a burn-in period. This stage induces appropriate inductive bias to avoid collapse pathologies observed during naive discrepancy minimization by random initialization.
• Fine-tuning: The model parameters are then updated to minimize differentiable, closed-form $L_2$-based discrepancy loss over all prefixes. Discrepancy objectives are parametrized by a choice of product-form kernel $k$ (see the paper’s Appendix), supporting star, symmetric, centered, periodic, and weighted variants. The loss combines prefix-wise discrepancies, optionally weighted to emphasize short or long prefixes.

This end-to-end pipeline yields a sequence generator that can be efficiently extended beyond the training prefix, with each segment maintaining low discrepancy.

Discrepancy Minimization Results

NeuroLDS is empirically validated—most notably in $d=4$ up to $N = 10^4$—with pretraining on Sobol’ and contemporary hyperparameter optimization (Optuna), against strong baselines: Sobol’, Halton, and nested-scrambled Sobol’. For all tested discrepancy metrics ($D_2^{\text{sym}}$, $D_2^{\text{star}}$, $D_2^{\text{ctr}}$), NeuroLDS achieves the lowest discrepancy for every reported sequence length and metric.

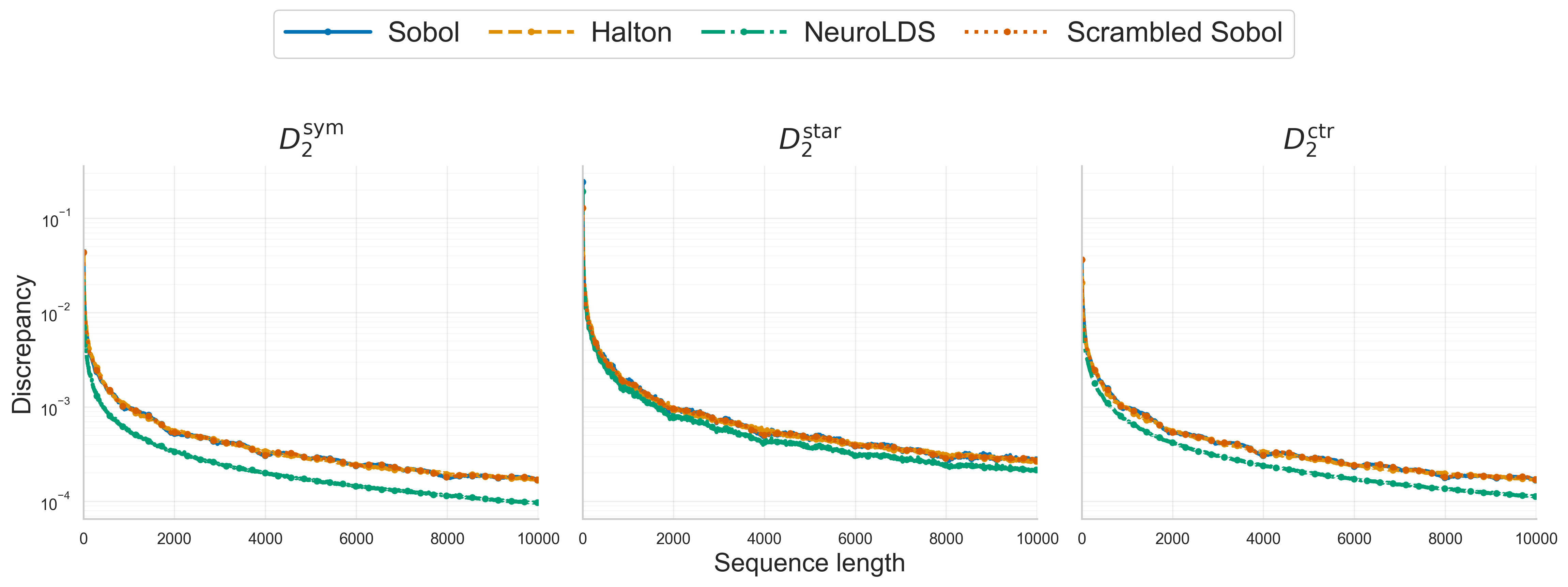
Figure 1: Comparison of $D_2$-type discrepancies for $4$D sequences up to $N=10,000$, showing NeuroLDS outperforming Sobol’, Halton, and scrambled Sobol’ for all metrics and lengths.

Further, the differences between NeuroLDS and classical sequences are especially pronounced at non-special values of $N$ (i.e., not powers of 2), which is a notable limitation of digital nets and sequences.

Downstream Applications

Quasi-Monte Carlo Integration

On the $d=8$ Borehole function—a standard benchmark for uncertainty quantification and sensitivity analysis—NeuroLDS (with coordinate-weighted discrepancy training informed by Sobol' sensitivity indices) consistently provides superior convergence and lower bias in integral estimates compared with Sobol’, Halton, and greedy set constructions. This is especially significant given the ill-conditioning and variable anisotropy typical in high-dimensional integrals.

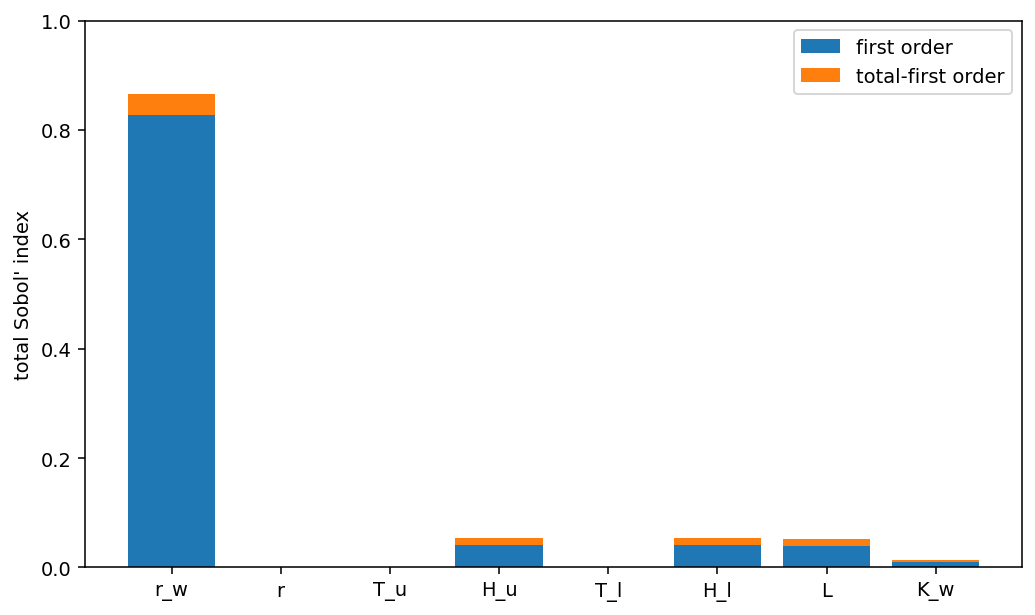
Figure 2: Sobol’ sensitivity indices for the Borehole function, guiding coordinate weight selection for NeuroLDS training.

Robot Motion Planning

In motion planning for high-dimensional kinematic chains (4D and 10D environments with narrow passages), using NeuroLDS for sequential sampling in RRT leads to higher success rates compared with uniform, Halton, or Sobol' sequencing. This holds across all tested passage widths, with gains maximal in the most constrained (lowest-volume) regimes.

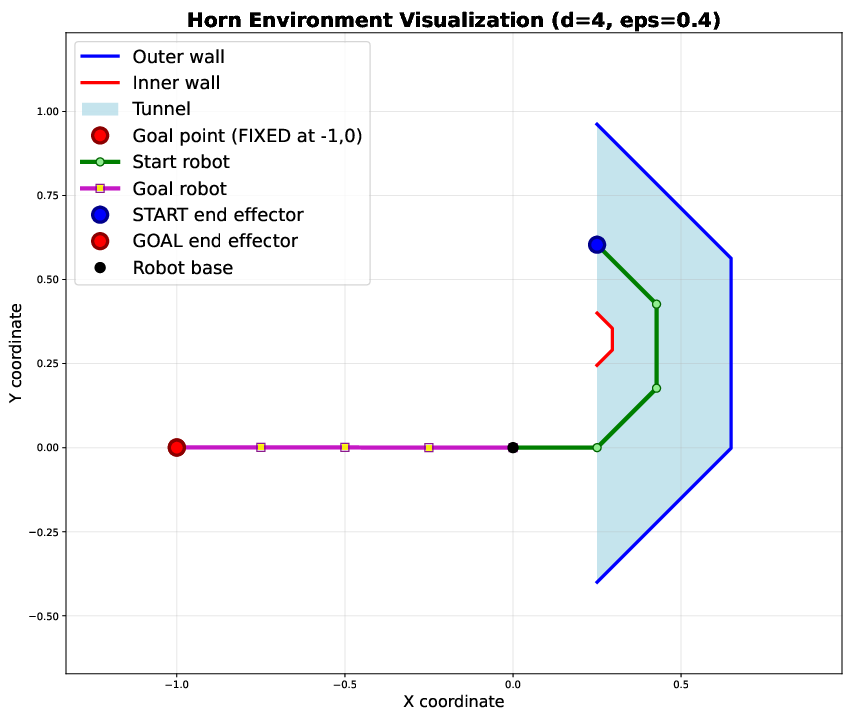
Figure 3: Configuration space visualization for a 4D kinematic chain in a semi-circular tunnel, a challenging scenario for sampling-based planners.

Scientific Machine Learning

When applied to parameter sampling for neural approximations to multivariate Black-Scholes PDEs, networks trained on NeuroLDS points deliver lower MSE prediction error than those trained on Sobol' or random points, regardless of the $L_2$-discrepancy variant used. This demonstrates compatibility with scientific machine learning scenarios characterized by nontrivial parameter-to-output mappings.

Ablation and Sensitivity Analyses

Key ablations highlight:

• Necessity of Pretraining: Direct optimization of discrepancy from random initializations leads to failure modes (collapse to domain corners); pretraining on a classic sequence is essential for stability.
• Sinusoidal Feature Bandwidth ($K$): Increasing $K$ reduces high-frequency fluctuations in sequence discrepancy across prefixes, enabling smoother, more consistent coverage.
• Depth and Nonlinearity: Deeper MLPs (multiple layers) are crucial; linear or shallow networks fail to capture the requisite digital logic and spatial uniformity.
• Choice of Prefix Weights: Uniform weights favor small prefixes; length-proportional weights favor long prefixes. Performance trade-offs are consistent with attributed loss emphasis.

  Figure 4: Comparison between uniform and length-proportional prefix weighting during fine-tuning, showing influence on early vs. late prefix discrepancy.

Theoretical and Practical Implications

NeuroLDS demonstrates that data-driven function approximation—when anchored in foundational concepts from QMC theory—can produce LDS with empirically measurable superiority to classical digital sequences and nets. The results point to the viability of neural architectures as differentiable, extensible sequence generators for a broad range of QMC and sampling-based computational paradigms.

An important conceptual implication is the observed dependence on well-initialized reference sequences. Despite the expressivity of neural sequence generators, their training dynamics and solution quality fundamentally rely on the arithmetic structure of classical LDS for stability and inductive guidance.

The approach is sufficiently modular to allow for alternative discrepancy losses (e.g., Stein discrepancies), suggesting possible extension to LDS targeting non-uniform measures or bespoke application domains.

Conclusion

NeuroLDS provides an extensible, neural-parameterized framework for generating LDS that matches or surpasses the performance of state-of-the-art algebraic constructions across discrepancy metrics and diverse tasks. Its design is distinguished by effective two-stage optimization, expressive index encoding, and hybridization with traditional QMC methodologies. The empirical results across integration, motion planning, and scientific ML demonstrate the broad applicability and competitive advantage of this approach. Prospective directions include extension to adaptive and weighted QMC methods, alternative discrepancy measures (Stein, energy), and integration with neural surrogate solvers for scientific computing workflows.