PromptCoT 2.0: Scaling Prompt Synthesis for Large Language Model Reasoning (2509.19894v1)

Abstract: LLMs are evolving from conversational systems into strong reasoners for tasks such as Olympiad mathematics and competitive programming. While scaling parameters and test-time computation has driven progress, a key bottleneck is the lack of high-quality training problems: human-curated datasets are costly and limited, while existing synthetic corpora are often too easy or narrow. PromptCoT 1.0 showed that injecting rationales into prompt synthesis increases problem difficulty. Building on this, we present PromptCoT 2.0, a scalable framework that replaces hand-crafted heuristics with an expectation-maximization (EM) loop, where rationales are iteratively refined to guide prompt construction. This produces problems that are both harder and more diverse than prior corpora. The synthetic prompts support two post-training regimes: (1) Self-Play, where strong models improve autonomously via verifiable feedback without stronger teachers; and (2) Supervised Fine-Tuning (SFT), where weaker models learn from teacher-distilled traces. Extensive experiments demonstrate the effectiveness of this approach. In self-play, applying PromptCoT 2.0 to Qwen3-30B-A3B-Thinking-2507 sets new state-of-the-art results at the 30B scale, with +4.4, +4.8, and +5.3 on AIME 24/25 and HMMT 25, +6.1 and +5.0 on LiveCodeBench v5/v6, and +35 Elo on Codeforces. In SFT, training Qwen2.5-7B-Instruct solely on synthetic prompts boosts accuracy to 73.1 (AIME 24), 65.6 (AIME 25), and 53.4 (LiveCodeBench v5), surpassing models trained on human or hybrid data. Analyses further confirm that PromptCoT 2.0 yields fundamentally harder and distributionally distinct problems. These results establish prompt synthesis as a new axis for scaling reasoning and position PromptCoT 2.0 as a scalable foundation for future open-source models. The implementation is available at https://github.com/inclusionAI/PromptCoT.

• The paper introduces an EM-based framework that iteratively refines rationales and prompts to produce challenging, diverse problems for LLM reasoning.
• It employs a two-model approach with an E-step reinforcing rationale generation and an M-step optimizing prompt synthesis to achieve superior accuracy gains.
• Empirical results demonstrate state-of-the-art performance on benchmarks like AIME and Codeforces, with significant improvements over conventional synthetic data methods.

PromptCoT 2.0: A Scalable EM-Based Framework for Rationale-Driven Prompt Synthesis

Introduction and Motivation

PromptCoT 2.0 addresses a central bottleneck in the development of reasoning-capable LLMs: the scarcity of high-quality, challenging, and diverse training problems. While scaling model parameters and test-time compute have yielded significant advances, further progress is increasingly constrained by the limitations of human-curated datasets and the inadequacy of existing synthetic corpora, which tend to be either too easy or insufficiently diverse. PromptCoT 2.0 extends the concept–rationale–prompt paradigm introduced in PromptCoT 1.0, replacing heuristic prompt engineering with a principled expectation–maximization (EM) optimization loop that iteratively refines rationales and synthesizes prompts. This framework is fully learnable, domain-agnostic, and scalable, enabling the generation of problems that are both more difficult and more distributionally diverse than prior approaches.

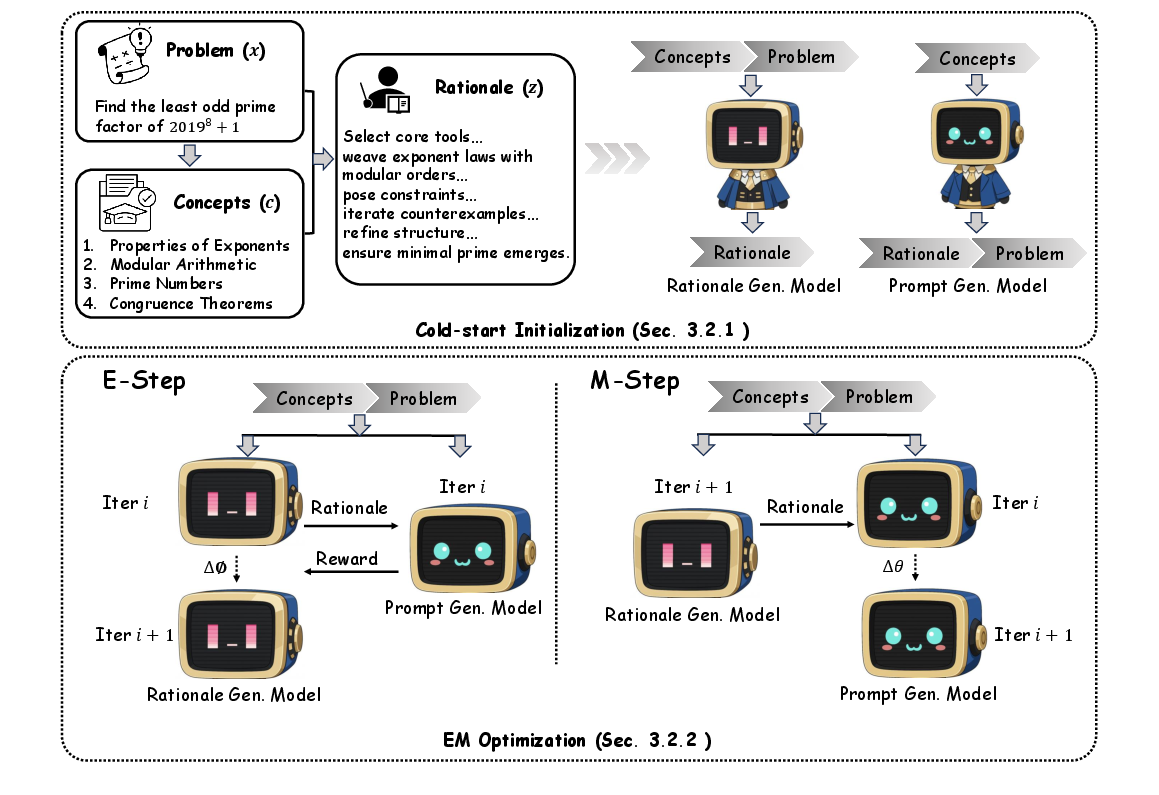
Figure 1: Overview of PromptCoT 2.0. The pipeline begins with open-source problems, annotates their concepts and rationales, and forms concept–rationale–problem triples for cold-starting the rationale and prompt generation models. EM optimization iteratively refines both models.

Methodology: EM-Guided Rationale–Prompt Synthesis

Problem Formulation

Prompt synthesis is formalized as modeling the conditional distribution $p(x \mid \mathbf{c})$, where $x$ is a prompt and $\mathbf{c}$ is a set of underlying concepts. PromptCoT 2.0 introduces a latent rationale variable $z$, factorizing the distribution as $$p(x \mid \mathbf{c}) = \sum_z p(x \mid z, \mathbf{c}) p(z \mid \mathbf{c})$$. Rationales serve as explicit, structured “thinking processes” that bridge the gap between abstract concepts and concrete problem statements, enabling the synthesis of more robust and challenging prompts.

EM Optimization Framework

PromptCoT 2.0 employs two models: a rationale generation model $q_\phi(z \mid \mathbf{c}, x)$ and a prompt generation model $p_\theta(z, x \mid \mathbf{c})$. The EM loop alternates between:

• E-step: Update $q_\phi$ to assign higher probability to rationales that maximize the joint likelihood of the rationale and prompt, i.e., $\log p_\theta(z, x \mid \mathbf{c})$.
• M-step: Update $p_\theta$ to maximize the expected joint log-likelihood over rationales sampled from $q_\phi$.

This iterative process ensures that rationales are both conceptually faithful and predictive of valid, challenging prompts, while the prompt generation model adapts to the evolving rationale distribution.

Practical Implementation

The pipeline consists of a cold-start initialization phase, where concept–rationale–problem triples are constructed using high-capacity instruction-tuned models, and an EM optimization phase, where both models are refined. The E-step leverages reinforcement learning with a reward corresponding to the joint log-likelihood, and the M-step uses supervised learning on sampled rationale–prompt pairs. This design enables the framework to scale across domains and problem types with minimal human intervention.

Post-Training Regimes: Self-Play and Supervised Fine-Tuning

PromptCoT 2.0 supports two complementary post-training regimes:

• Self-Play: For strong models, synthesized prompts with verifiable feedback enable autonomous improvement without external teachers. The model generates candidate solutions, receives automatic rewards (e.g., passing unit tests or matching boxed answers), and updates its parameters to maximize expected reward using methods such as DPO or PPO.

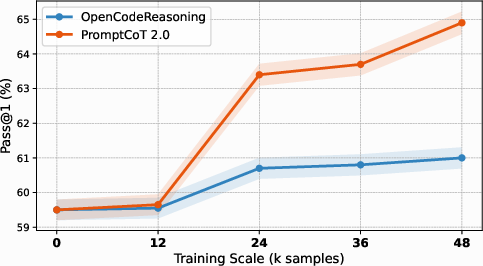
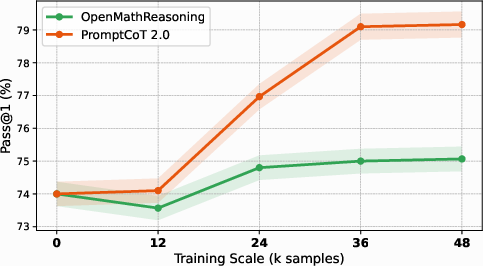
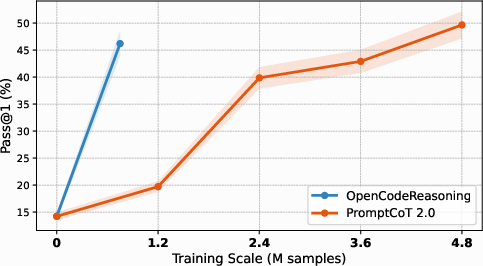
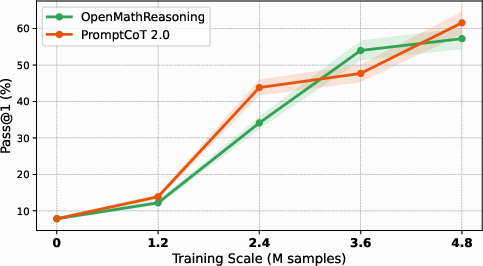
Figure 2: Self-play on code benchmarks. PromptCoT 2.0 enables consistent improvements over baselines as models iteratively learn from synthesized, verifiable problems.

• Supervised Fine-Tuning (SFT): For weaker models, a strong teacher generates reasoning traces for the synthesized prompts, and the student is trained via supervised learning. This regime allows models with limited initial reasoning ability to benefit from the high-quality synthetic data.

Empirical Results and Analysis

Performance on Reasoning Benchmarks

PromptCoT 2.0 establishes new state-of-the-art results at the 30B parameter scale across six challenging benchmarks, including AIME 24/25, HMMT Feb 25, LiveCodeBench v5/v6, and Codeforces. Notably, in the self-play setting, Qwen3-30B-A3B-Thinking-2507 trained with PromptCoT 2.0 achieves +4.4, +4.8, and +5.3 accuracy improvements on AIME 24/25 and HMMT 25, +6.1 and +5.0 on LiveCodeBench v5/v6, and +35 Elo on Codeforces. In the SFT setting, Qwen2.5-7B-Instruct trained solely on synthetic prompts outperforms models trained on human or hybrid data, with accuracy gains up to 73.1 (AIME 24), 65.6 (AIME 25), and 53.4 (LiveCodeBench v5).

Scaling and Data Efficiency

PromptCoT 2.0 demonstrates superior data efficiency and scaling properties compared to curation-based baselines. Performance continues to improve with additional synthesized data, whereas baselines saturate early. The EM-guided rationale–prompt synthesis produces higher-quality problems that yield sustained gains as the training set grows.

Distributional and Difficulty Analysis

Multidimensional scaling (MDS) of dataset-level embeddings reveals that PromptCoT 2.0’s synthesized problems are distributionally distinct from existing open-source corpora, indicating greater diversity in linguistic and structural features.

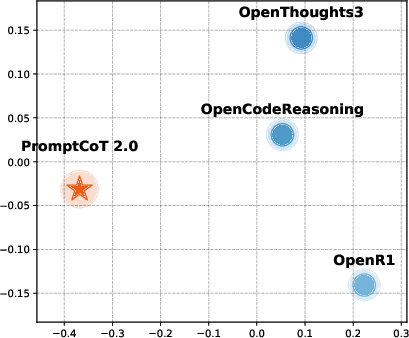
Figure 3: MDS visualization for code datasets. PromptCoT 2.0 occupies a distinct region, reflecting substantial distributional differences from prior corpora.

Difficulty analysis shows that PromptCoT 2.0 produces the most challenging problems, as measured by lower zero-shot accuracy of strong LLMs and longer reasoning traces required for solution. This is achieved without explicit difficulty filtering, in contrast to other datasets.

Ablation and EM Optimization Analysis

Ablation studies confirm that both the cold-start and EM optimization stages are essential for optimal performance. Removing either component leads to significant degradation, particularly on the most challenging benchmarks. Tracking negative log-likelihood (NLL) during EM optimization demonstrates that iterative rationale refinement via the E-step yields sharper and deeper likelihood improvements.

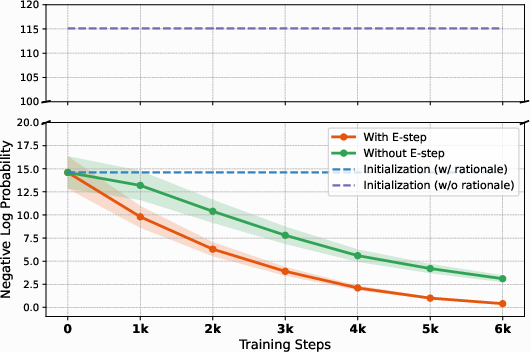
Figure 4: NLL trajectories during EM optimization. The full EM procedure with iterative rationale refinement achieves lower NLL than variants without the E-step or without rationales.

Case Studies: Rationale–Prompt Generation

The framework is illustrated with case studies spanning number theory, 3D geometry, and programming. In each case, foundational concepts are identified, a detailed rationale is constructed, and a challenging problem is synthesized. These examples demonstrate the capacity of PromptCoT 2.0 to generate problems that require multi-step reasoning and are suitable for high-level benchmarks such as AIME and Codeforces.

Implications and Future Directions

PromptCoT 2.0 establishes prompt synthesis as a new axis for scaling LLM reasoning, independent of brute-force increases in model size or compute. The EM-based rationale–prompt co-optimization paradigm is extensible to new domains and problem types, and the resulting synthetic corpora provide a scalable foundation for both open-source and proprietary models. The framework’s ability to generate fundamentally harder and more diverse problems has direct implications for advancing agentic intelligence, scientific discovery, and other domains requiring robust reasoning.

Future work includes extending the EM-based synthesis to multimodal prompts, integrating richer verification signals for self-play, and exploring joint optimization of prompt synthesis and model post-training in a fully self-evolving loop.

Conclusion

PromptCoT 2.0 presents a principled, scalable, and domain-agnostic framework for rationale-driven prompt synthesis, leveraging EM optimization to generate high-quality, challenging, and diverse problems for LLM reasoning. Empirical results demonstrate substantial improvements over existing baselines in both self-play and SFT regimes, with strong evidence of superior data efficiency, scaling, and distributional diversity. The approach positions prompt synthesis as a central driver for the next generation of reasoning-capable LLMs and provides a robust foundation for future research in autonomous, verifiably strong LLMs.