- The paper introduces a reinforcement learning framework (G1) that uses synthetic graph tasks and a large curated dataset to boost LLMs' graph reasoning capabilities.
- It employs a two-phase training pipeline, combining supervised fine-tuning with Group Relative Policy Optimization, leading to efficient performance gains.
- Empirical results show that smaller G1 models outperform larger baselines on various graph tasks, achieving strong generalization and transferability.
G1: Teaching LLMs to Reason on Graphs with Reinforcement Learning
Motivation and Problem Statement
LLMs have demonstrated strong general reasoning capabilities, but their performance on graph-theoretic tasks remains suboptimal, with state-of-the-art models achieving only moderate accuracy on even basic graph connectivity problems. This limitation is critical, as graph reasoning underpins a wide range of applications in science, engineering, and knowledge representation. Prior approaches—such as instruction tuning, preference alignment, and graph foundation model pretraining—are constrained by the lack of large-scale, diverse, and universally represented graph datasets, and often fail to generalize across graph types and encoding schemes.
The G1 framework addresses these challenges by leveraging Reinforcement Learning (RL) on synthetic graph-theoretic tasks, demonstrating that RL can elicit latent graph reasoning abilities in pretrained LLMs without reliance on human-annotated data. The approach is enabled by the construction of the largest graph reasoning dataset to date, comprising 50 diverse tasks and 100k training samples derived from real-world graphs.
Dataset Construction and Task Diversity
The G1 dataset is curated from real-world graphs using the Network Repository, with subgraphs sampled to fit LLM context windows (5–35 nodes). Tasks span a spectrum of complexity, from basic properties (node counting, edge existence) to NP-hard problems (maximal independent set, traveling salesman, isomorphic mapping). Each task is accompanied by ground-truth answers or algorithmic verification programs, enabling rule-based reward attribution for RL.
Graph encoding is standardized to edge list format, facilitating consistent input representation. The dataset supports both training and benchmarking, and is open-sourced for reproducibility and further research.
RL Training Pipeline and Reward Design
G1 employs a two-phase training pipeline:
- Supervised Fine-Tuning (SFT): An optional warm-up phase using either direct question-answer pairs (Direct-SFT) or chain-of-thought trajectories (CoT-SFT) generated via rejection sampling from a stronger teacher model. This phase is critical for initializing the model on challenging tasks where base accuracy is low.
- Reinforcement Learning (RL): The core phase utilizes Group Relative Policy Optimization (GRPO), rewarding correct rollouts based on strict value matching, Jaccard index for set answers, and algorithmic verification for multi-solution tasks. The KL penalty to the reference policy prevents overfitting and catastrophic forgetting.
The RL phase is highly data-efficient, requiring only 300 steps with batch size 512 on 8×A800 GPUs for 3B/7B models. Hyperparameters are tuned for stability and exploration, with entropy regularization to encourage diverse solution strategies.
Empirical Results and Scaling Behavior
G1 models exhibit substantial improvements over baselines and prior graph-specialized models across all difficulty levels. Notably, G1-3B and G1-7B outperform Qwen2.5-72B-Instruct and Llama-3.1-70B-Instruct by wide margins, despite being 20× smaller in parameter count. G1-7B achieves 66.16% average accuracy, surpassing GPT-4o-mini by 18.56% and matching OpenAI o3-mini.
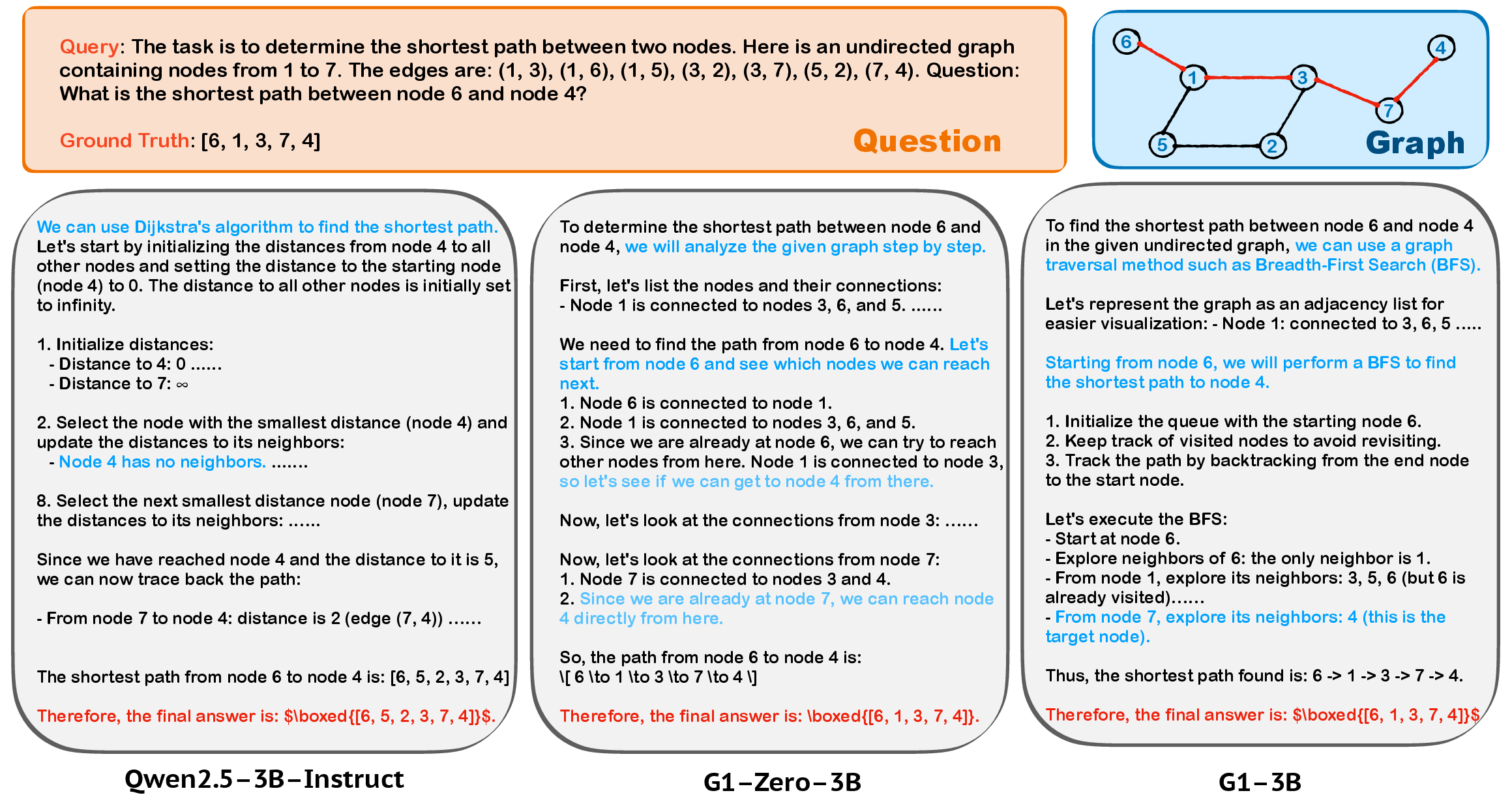
Figure 1: An intuitive illustration of the differences in solution strategies employed by Qwen2.5-3B-Instruct, G1-Zero-3B, and G1-3B for a shortest path problem.
Scaling to larger models (G1-Zero-32B) and larger graphs (36–100 nodes) demonstrates robust zero-shot generalization, with G1-32B achieving 75.06% average accuracy and strong transfer to harder problem categories. The approach is bottlenecked only by LLM context window limits, not by reasoning capability.
Transferability and Generalization
G1 models generalize strongly to unseen graph tasks, domains, and encoding schemes, outperforming models specifically trained on GraphWiz and GraphArena benchmarks. Transfer to real-world node classification and link prediction tasks (Cora, PubMed) is also robust, with G1-7B achieving 87.29% average accuracy.
Importantly, RL training on graph-theoretic tasks does not compromise general reasoning ability on mathematics (GSM8K, MATH) and multi-task benchmarks (MMLU-Pro). In several cases, G1-7B surpasses the base model on non-STEM disciplines, indicating synergistic improvement in reasoning skills.
Training Analysis and Strategy Optimization
Analysis of training factors reveals that Direct-SFT is a strong baseline for pattern memorization, but RL (especially with CoT-SFT initialization) confers superior scaling and generalization. Reward signal imbalance across task difficulty can be mitigated by dynamic difficulty scheduling or reward weighting, with models trained exclusively on hard tasks generalizing back to easier ones.
Case studies on shortest path problems show that RL-trained models adapt their reasoning strategies, favoring BFS and intuitive search over computationally complex algorithms like Dijkstra, aligning solution methods with model capabilities.
Limitations and Future Directions
G1 inherits sample inefficiency from GRPO, requiring extensive rollouts for NP-hard tasks. Generalization to highly domain-specific applications (e.g., molecular property prediction, tabular/time-series data) remains untested. Scaling to graphs with thousands of nodes is currently limited by context window constraints, but advances in long-context LLMs may alleviate this.
Future work should explore dynamic difficulty scheduling, integration of visual graph inputs, and adaptation to practical domains such as logistics and knowledge graph reasoning.
Conclusion
G1 establishes RL on synthetic graph-theoretic tasks as an efficient, scalable paradigm for eliciting graph reasoning abilities in LLMs. The approach combines the strengths of pretrained LLMs with abundant, automatically generated data, achieving strong performance, generalization, and transferability. These results suggest a shift away from reliance on heterogeneous real-world graph datasets, paving the way for versatile AI systems capable of sophisticated reasoning across structured modalities.
