- The paper introduces SRE, which integrates semantic reformulations and hybrid semantic clustering to enhance hallucination detection in QA tasks.
- It demonstrates robust performance with an AUROC of 0.887 on benchmarks like SQuAD and TriviaQA, outperforming existing methods.
- Parameter sensitivity analysis identifies optimal reformulation counts and sampling configurations, emphasizing the method's practical tuning.
Introduction
The paper addresses the challenge of hallucination detection in LLMs within the domain of question answering (QA). Hallucinations, or outputs that are fluent yet factually incorrect, are problematic due to epistemic uncertainty. Semantic Reformulation Entropy (SRE) is introduced as a method to improve uncertainty estimation by addressing the limitations present in existing entropy-based semantic-level methods. These limitations include the narrow sampling space and the instability of natural language inference (NLI)-based clustering.
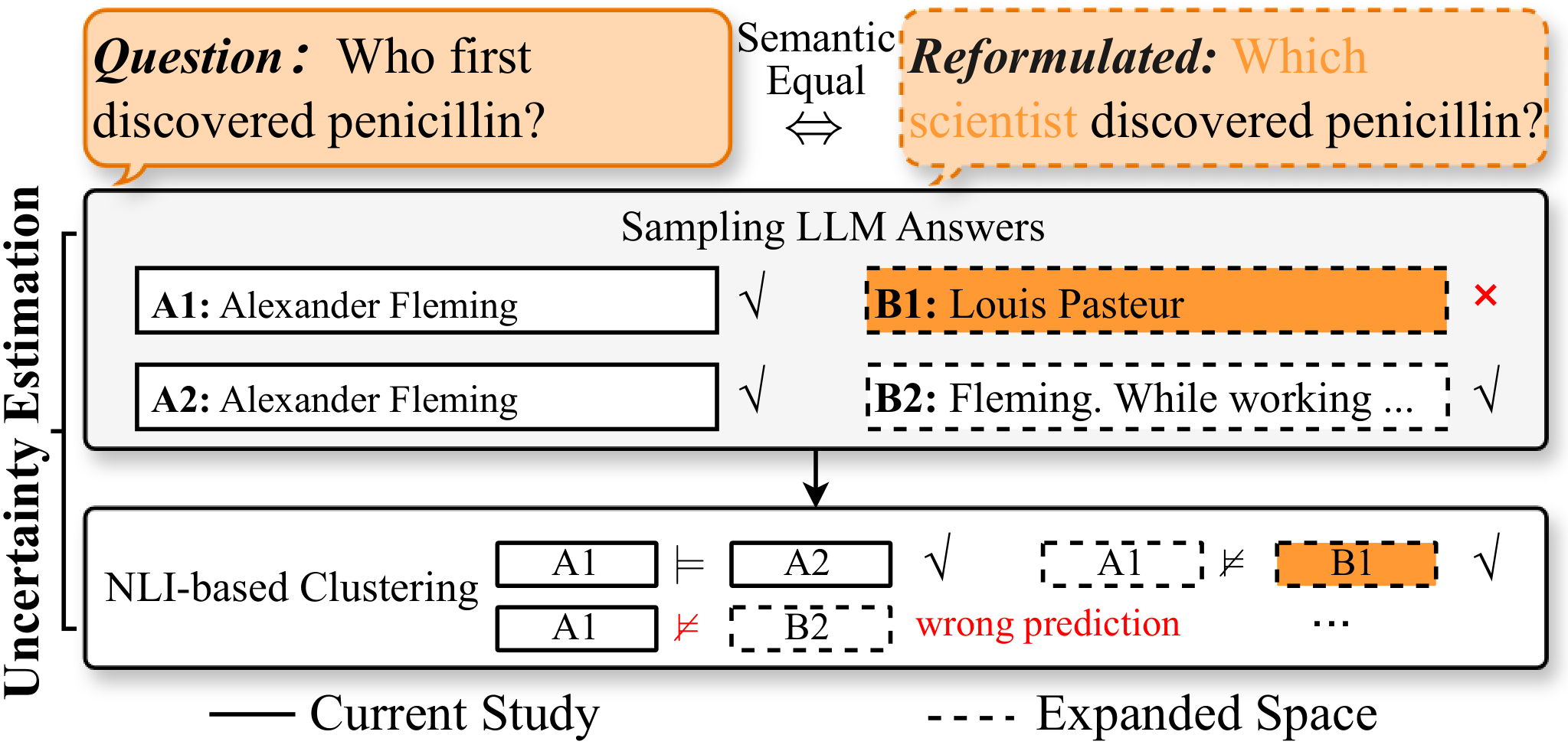
Figure 1: Key limitations in QA uncertainty estimation: limited sampling space and fragile NLI-based clustering.
Methodology
The concept of SRE extends the previous semantic entropy approaches by enriching both the input and output sides of uncertainty estimation. On the input side, semantic reformulation systematically generates faithful paraphrases of the input question. These reformulations are used to mitigate the effect of superficial decoder patterns on uncertainty estimation, thereby expanding the estimation space. Each paraphrase is evaluated with cosine similarity to ensure diversity and fidelity.
Hybrid Semantic Clustering
The output side employs hybrid semantic clustering (HSC) which combines exact matches, embedding similarities, and bidirectional NLI results to stabilize semantic grouping. This progressive, energy-based clustering method ensures that variable-length or semantically complex outputs are more accurately grouped, creating a foundation for robust uncertainty estimation.
Combined Framework
The combination of semantic reformulation and hybrid clustering in SRE leads to improved capture of epistemic uncertainty at the semantic level. The approach leverages both input diversification and multi-signal clustering, providing a reliable entropy estimation framework across different QA settings.
Experimental Results
SRE was evaluated on public QA benchmarks, namely SQuAD and TriviaQA, in both open-domain and extractive QA settings. The results indicate that SRE surpasses existing strong baselines, achieving a maximum AUROC of 0.887, demonstrating superior performance in hallucination detection.
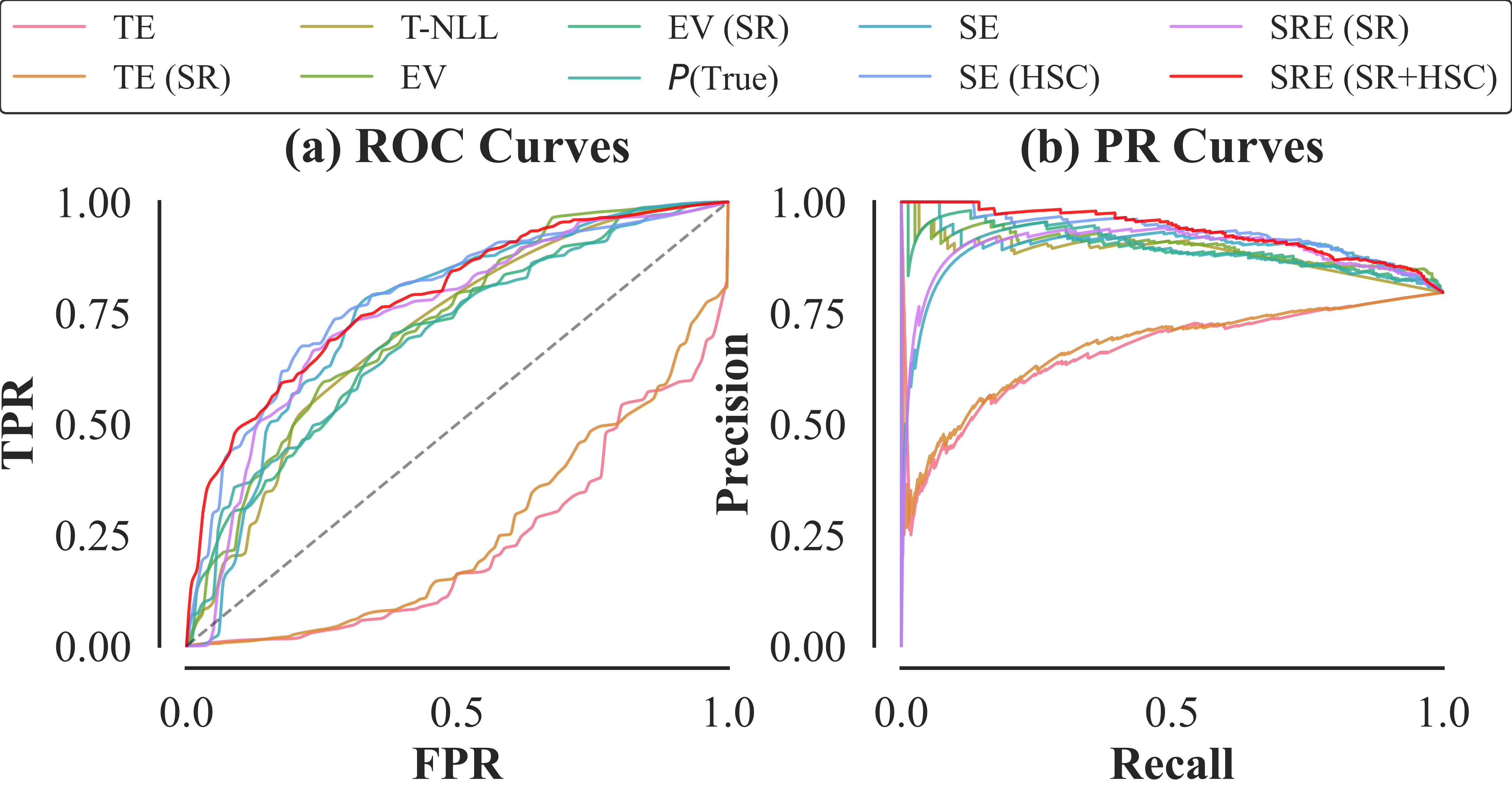
Figure 2: ROC (a) and PR (b) curves of all methods on SQuAD (no context) with Llama3-8B.
Ablation studies show that the improvements are primarily driven by HSC rather than SR, highlighting the impact of refined clustering processes. Additionally, the distribution of uncertainty scores exhibited clearer separation with SRE, corroborated by metrics such as Cohen's d and Wasserstein distance, confirming the method's efficacy.
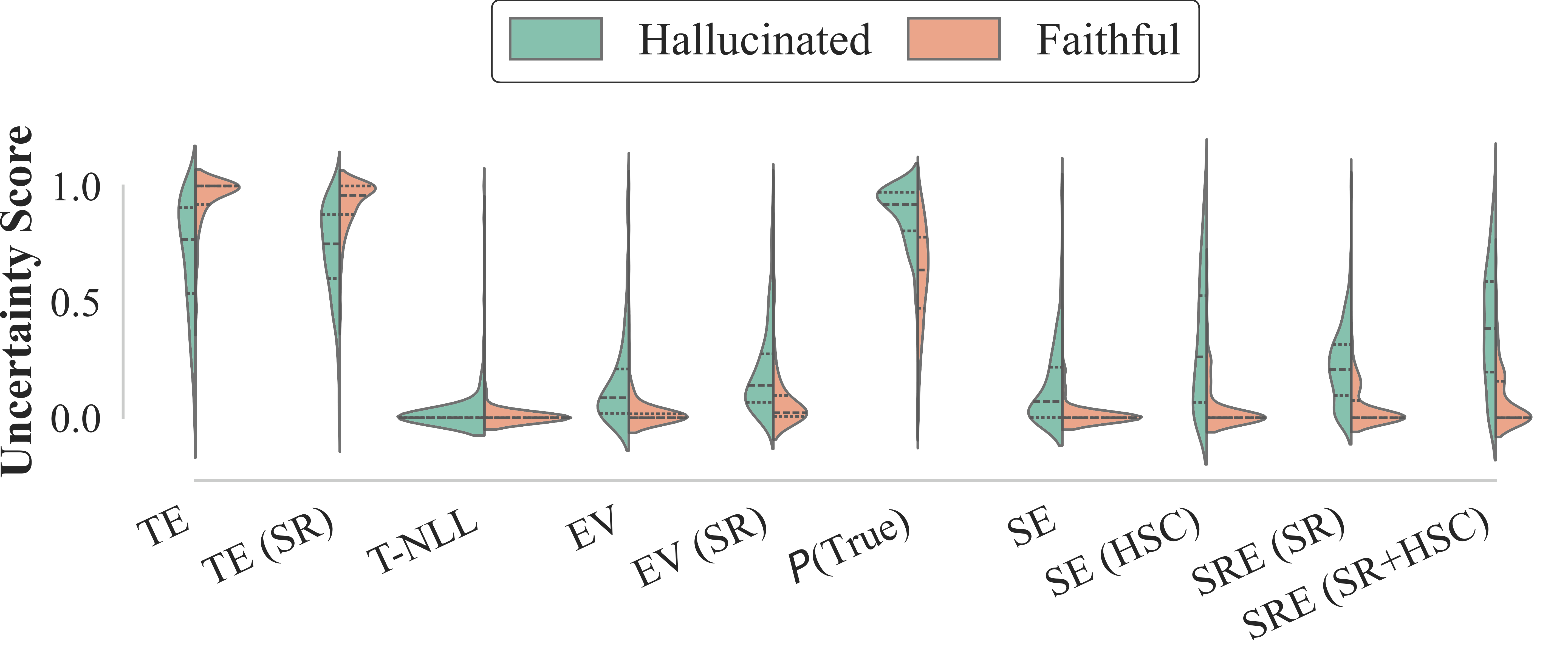
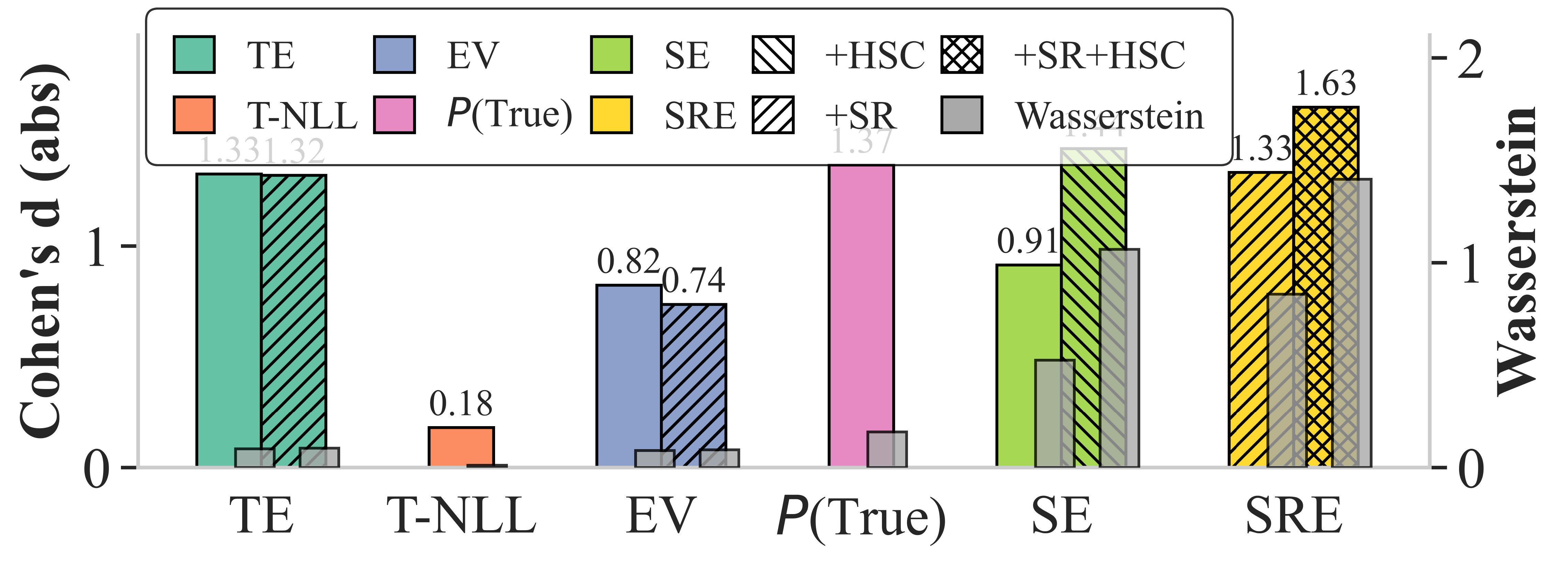
Figure 3: Uncertainty distributions of hallucinated vs. faithful samples for SRE and baselines.
Parameter Sensitivity Analysis
Detailed sensitivity analysis of key parameters, such as the number of reformulations and sampling temperature, was performed, showing that optimal performance is achieved with specific configurations (e.g., N=3 reformulations, K=8 samples per reformulation, and T=0.8 sampling temperature).
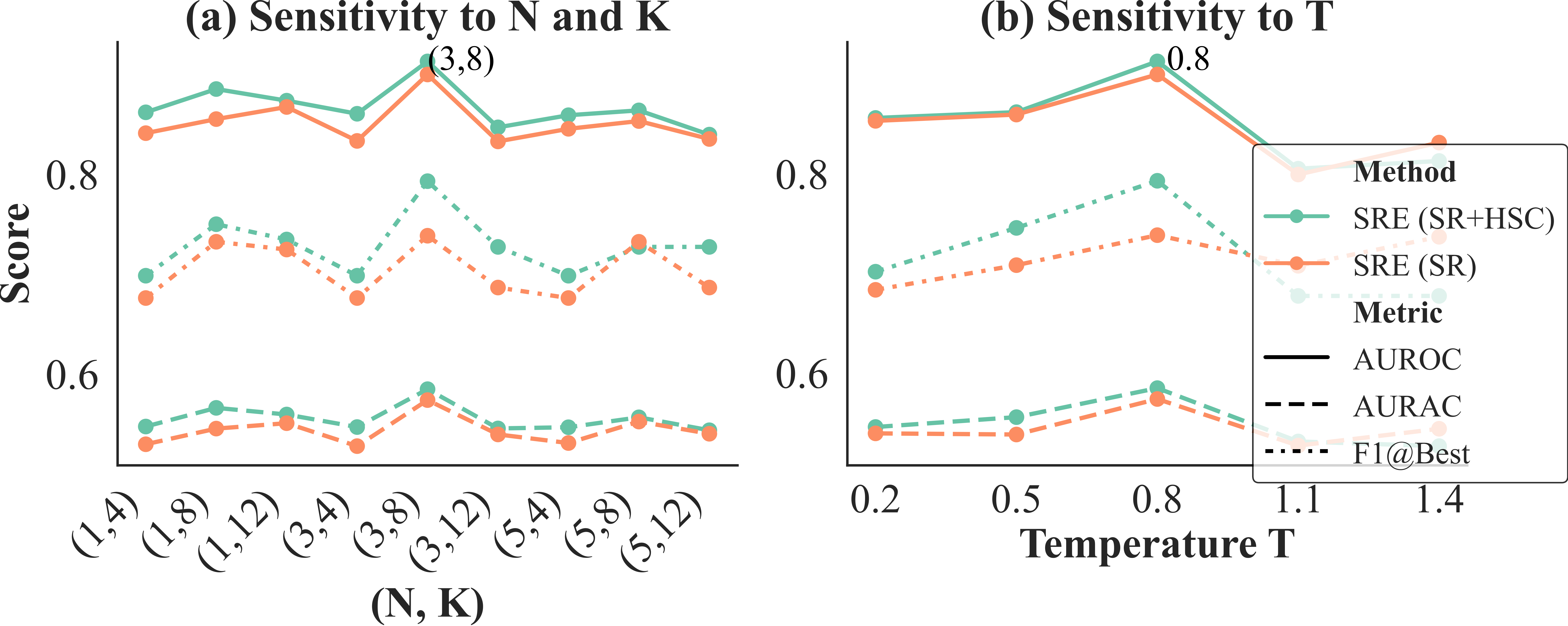
Figure 4: Parameter sensitivity analysis of SRE.
Conclusion
The development of SRE presents a significant step in enhancing the reliability of LLMs by expanding the uncertainty estimation framework. By integrating semantic reformulations and refined clustering, SRE achieves robust hallucination detection, paving the way for more dependable application of LLMs in QA tasks. Future work may involve optimizing the computational efficiency of the reformulation and clustering processes, which currently rely on resource-intensive LLM sampling and NLI computation. This research underscores the potential of systematically expanding the uncertainty space combined with precise estimation methods in improving model reliability.




