Semantic Entropy Probes: Robust and Cheap Hallucination Detection in LLMs

Abstract: We propose semantic entropy probes (SEPs), a cheap and reliable method for uncertainty quantification in LLMs. Hallucinations, which are plausible-sounding but factually incorrect and arbitrary model generations, present a major challenge to the practical adoption of LLMs. Recent work by Farquhar et al. (2024) proposes semantic entropy (SE), which can detect hallucinations by estimating uncertainty in the space semantic meaning for a set of model generations. However, the 5-to-10-fold increase in computation cost associated with SE computation hinders practical adoption. To address this, we propose SEPs, which directly approximate SE from the hidden states of a single generation. SEPs are simple to train and do not require sampling multiple model generations at test time, reducing the overhead of semantic uncertainty quantification to almost zero. We show that SEPs retain high performance for hallucination detection and generalize better to out-of-distribution data than previous probing methods that directly predict model accuracy. Our results across models and tasks suggest that model hidden states capture SE, and our ablation studies give further insights into the token positions and model layers for which this is the case.

• The paper introduces Semantic Entropy Probes (SEPs) that leverage hidden state analysis to predict semantic uncertainty in LLM outputs.
• It demonstrates that SEPs significantly cut computational overhead by eliminating the need for multiple generation samples during inference.
• SEPs outperform traditional accuracy probes in hallucination detection and generalize better across various models and tasks.

Semantic Entropy Probes: Robust and Cheap Hallucination Detection in LLMs

Introduction

The reliability of LLMs is undermined by their tendency to hallucinate—generating plausible but incorrect content. The paper introduces Semantic Entropy Probes (SEPs) as a novel method for hallucination detection in LLMs. Unlike conventional methods that rely on semantic entropy by sampling multiple model generations, SEPs estimate semantic uncertainty from hidden states, significantly reducing computational overhead.

Methodology

Semantic Entropy and Its Estimation

Semantic entropy measures uncertainty in LLM outputs by clustering semantically similar responses. The approach involves sampling model generations and assessing their semantic equivalence using Natural Language Inference (NLI) models. The computed semantic entropy is instrumental as a supervisory signal for training SEPs.

Semantic Entropy Probes (SEPs)

SEPs are linear probes trained to predict semantic entropy from the hidden states of a single generation. They provide a computationally efficient alternative to existing methods by circumventing the need for multiple generation samples at inference time. By training SEPs on hidden states, the paper posits that SELs naturally encode model uncertainty over semantic meanings.

Experimental Setup

SEPs were evaluated across diverse datasets (e.g., TriviaQA, SQuAD, BioASQ) and models (e.g., Llama-2 and Llama-3 series). Both in-distribution and out-of-distribution settings were investigated to benchmark SEP performance against baselines like accuracy probes and sampling-based approaches.

Results and Analysis

Capturing Semantic Entropy

Across models and tasks, SEPs consistently predicted semantic entropy with high fidelity, especially in mid-to-late layers (Figure 1). This indicates that model hidden states inherently encode semantic uncertainty, allowing SEPs to effectively capture this information.

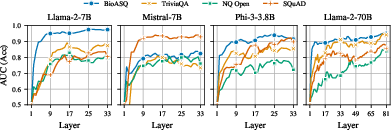
Figure 1: Semantic Entropy Probes (SEPs) achieve high fidelity for predicting semantic entropy from mid-to-late layers.

Moreover, SEPs can predict semantic entropy even before generating responses, offering further cost reductions by computing uncertainty with a single forward pass (Figure 2).

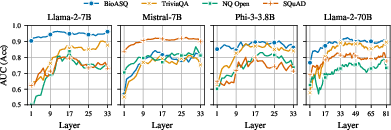
Figure 2: Semantic entropy predicted from the hidden states of the last input token without generating new tokens.

Hallucination Detection

SEPs surpassed accuracy probes in detecting hallucinations when generalizing to new tasks (Figure 3). Although they do not match the performance of computationally expensive sampling-based methods, SEPs present a cost-effective solution that balances performance and efficiency.

Figure 3: SEPs outperform accuracy probes for hallucination detection when generalizing to unseen tasks.

SEPs also demonstrated their effectiveness in long-form generation scenarios (Figure 4), confirming that semantic uncertainty is retained across different generative contexts.

Figure 4: SEPs capture semantic entropy for long generations in Llama-2-70B and Llama-3-70B across layers.

Discussion and Implications

SEPs exhibit robust performance across models and scenarios, highlighting the potential of hidden states as a rich source for uncertainty estimation. The findings suggest that semantic entropy is a more natural and generalizable signal than accuracy, leading to superior generalization capabilities. This opens avenues for future research, such as scaling SEP training with diverse data sources to enhance performance further.

Conclusion

Semantic Entropy Probes offer a compelling, resource-efficient alternative for hallucination detection in LLMs. By leveraging hidden states, SEPs provide valuable insights into model behavior and demonstrate substantial promise for real-world AI applications, where cost and reliability are pivotal.

Figure 5: SEPs generalize better to new tasks than accuracy probes, offering a balanced tradeoff between cost and performance.