Geodesic clustering of zeros of Eisenstein series for congruence groups (2509.16108v1)

Abstract: We consider a set of generators for the space of Eisenstein series of even weight $k$ for any congruence group $\Gamma$ and study the set of all of their zeros taken for $\Gamma(1)$-conjugates of $\Gamma$ in the standard fundamental domain for $\Gamma(1)$. We describe (a) an upper bound $\kappa_\Gamma + O(1/k)$ for their imaginary part; (b) a finite configuration of geodesics segments to which all zeros converge in Hausdorff distance as $k \rightarrow \infty$; (c) a finite set containing all algebraic zeros for all weights. The bound in (a) depends on the (non-)vanishing of a new generalization of Ramanujan sums. The proof of (b) originates in a method used to study phase transitions in statistical physics. The proof of (c) relies on the theory of complex multiplication. The results can be made quantitative for specific groups. For $\Gamma=\Gamma(N)$ with $4 \nmid N$, $\kappa_\Gamma=1$ and the zeros tend to the unit circle, whereas if $4 \mid N$, $\kappa_\Gamma=2$ and the limit configuration includes parts of vertical geodesics and circles of radius $2$. In both cases, the only algebraic zeros are at $\mathrm{i}$ and $\exp(2\pi \mathrm{i}/3)$ for sufficiently large $k$. For $\Gamma(N)$ with $N$ odd, we use finer estimates to prove a trichotomy for the exact `convergence speed' of the zeros to the unit circle, as well as angular equidistribution of the zeros as $k \rightarrow \infty$.

• The paper provides a natural generating set for Eisenstein series and demonstrates sharp imaginary part bounds on their zeros.
• It shows that as the weight increases, zeros converge in Hausdorff distance to specific geodesic segments in the upper half-plane.
• Quantitative analysis includes angular equidistribution, algebraic zero characterization, and precise bounds derived from Kluyver sums.

Geodesic Clustering of Zeros of Eisenstein Series for Congruence Groups

Introduction and Main Results

This paper provides a comprehensive analysis of the geometric and arithmetic distribution of zeros of Eisenstein series associated to congruence subgroups $\Gamma$ of $\mathrm{SL}_2(\mathbb{Z})$, with a focus on principal congruence groups $\Gamma(N)$ and their generalizations. The authors construct a natural generating set for the Eisenstein space $E_k(\Gamma)$ in even weight $k$, and paper the union of zeros of all such series, conjugated by $\Gamma(1)$, within the standard fundamental domain $F$.

The central results are:

• Imaginary Part Bounds: For each congruence group $\Gamma$, there exists a sharp upper bound $\kappa_\Gamma + O(1/k)$ for the imaginary part of any zero of Eisenstein series of weight $k$.
• Geodesic Clustering: As $k \to \infty$, the zeros converge in Hausdorff distance to a finite union of geodesic segments in the upper half-plane, determined explicitly by the group structure and weight.
• Algebraic Zeros: For sufficiently large $k$, all algebraic zeros are contained in a finite set, typically only at $i$ and $\exp(2\pi i/3)$, with explicit bounds on possible discriminants.
• Equidistribution and Convergence Speed: For odd $N$, zeros exhibit angular equidistribution and a trichotomy in convergence speed to the unit circle.

These results are made quantitative for specific groups, with explicit constants and configurations described.

Eisenstein Series Generators and Basis Structure

The authors introduce a generating set for $E_k(\Gamma(N))$ via

$$E_k^{a,b}(z) = \sum_{(m,n) \neq (0,0)} \frac{e(an-bm)}{(mz+n)^k}$$

with $(a,b) \in (N^{-1}\mathbb{Z}/\mathbb{Z})^2$. This set is a discrete Fourier transform of Hecke's classical basis, and is particularly amenable to geometric analysis of zeros due to the explicit control over dominant terms in the upper half-plane.

A key technical result is that the set $\{E_k^{a,b}\}$ indexed by primitive $(a,b)$ forms a basis for $E_k(\Gamma(N))$ if and only if $N$ is squarefree, established via subdeterminants of character tables.

Imaginary Part Bounds and Kluyver Sums

The imaginary part bound for zeros is governed by a generalization of Ramanujan sums, termed Kluyver sums:

$$\rho_\Gamma^{a,b}(j) = 2 \sum_{g \in \Gamma(N) \backslash \Gamma} \cos(2\pi j (\alpha a + \gamma b))$$

where $$g = \begin{pmatrix} \alpha & \beta \ \gamma & \delta \end{pmatrix}$$. The minimal $j$ for which $\rho_\Gamma^{a,b}(j) \neq 0$ determines $\kappa_\Gamma^{a,b}$, and the maximal such over all conjugates gives $\kappa_\Gamma$.

For $\Gamma(N)$:

• If $4 \nmid N$, $\kappa_\Gamma = 1$.
• If $4 \mid N$, $\kappa_\Gamma = 2$.

This leads to the sharp bound $\operatorname{Im}(z) < \kappa_\Gamma + O(1/k)$ for all zeros.

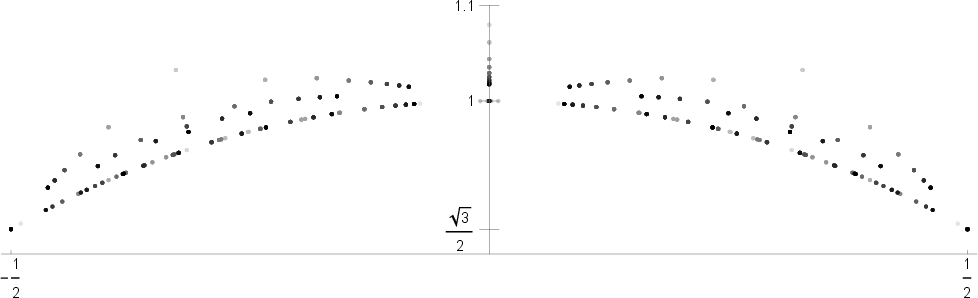
Figure 1: Distribution of zeros for $\Gamma(3)$, showing clustering near the unit circle as weight increases.

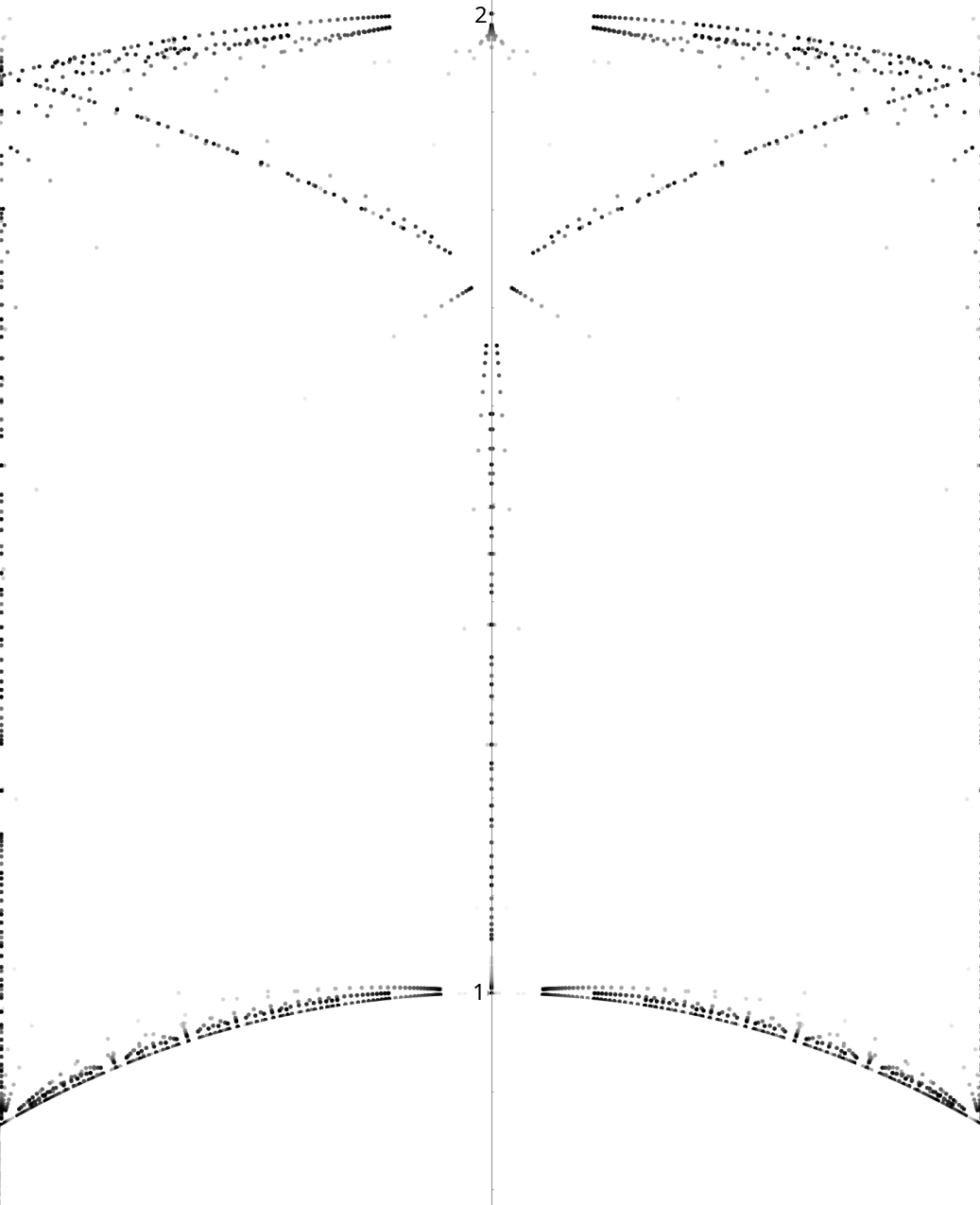
Figure 2: Zeros for $\Gamma(8)$, illustrating clustering near circles of radius $2$ and vertical geodesics for $4 \mid N$.

Geodesic Clustering and Hausdorff Limits

The main geometric result is that as $k \to \infty$, the zeros of Eisenstein series for $\Gamma$ converge in Hausdorff distance to a finite union of geodesic segments in $H$. These segments are explicitly described as loci where $|mz+n| = |m'z+n'|$ for pairs $(m,n), (m',n')$ in a finite index set determined by the group and Kluyver sums.

For $\Gamma(N)$:

• If $4 \nmid N$, the limit set is the lower arc of the unit circle in $F$.
• If $4 \mid N$, the limit includes arcs of circles of radius $2$ centered at $0, \pm 1$ and vertical segments.

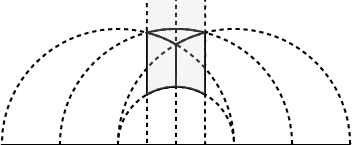
Figure 3: Geodesic completion of the Hausdorff limit of zeros for $\Gamma(N)$, with $N$ odd (left) and $N$ divisible by $4$ (right).

Transcendence and Algebraic Zeros

Using Schneider's theorem and complex multiplication, the authors prove that for large $k$, all algebraic zeros are CM points with discriminant $|D| \leq 4\kappa_\Gamma^2$. For $\kappa_\Gamma = 1$, only $i$ and $\rho$ can occur; for $\kappa_\Gamma = 2$, a finite explicit list is given.

Explicit bounds are provided: for $N$ not divisible by $4$ and $k > 5\log(54N)$, all zeros have $\operatorname{Im}(z) < 1 + \log(13N)/k$ and only $i, \rho$ are algebraic.

Convergence Speed and Angular Equidistribution

For $\Gamma(N)$ with $N$ odd, the zeros exhibit a trichotomy:

• Most zeros are $O(1/k)$-close to the unit circle.
• A small number are exponentially close to $i$ or $\rho$.
• Some zeros lie exactly on the arc for special choices of $(a,b)$.

Angular equidistribution is established: the arguments of zeros in $F$ converge weakly to the Haar measure on the arc as $k \to \infty$, with discrepancy $O(\log N / k)$.

Methodology and Proof Techniques

The analysis combines:

• Truncation and asymptotic estimates of Eisenstein series.
• Explicit control of remainder terms via lattice point counting and integral bounds.
• Application of Sokal's method for Hausdorff limits of zero sets, adapted to infinite sums.
• Arithmetic arguments using Galois actions and CM theory for transcendence results.
• Rouché-type arguments and sign-change techniques for zero counting and localization.

  Figure 4: Limit configuration of zeros for a family of functions, illustrating the semi-algebraic nature of the Hausdorff limit.

  

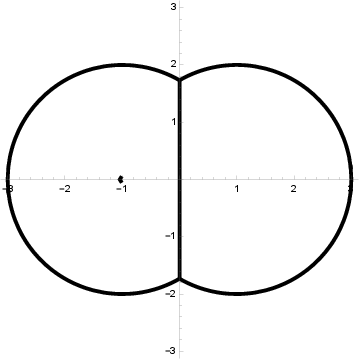
  Figure 5: Limit configuration for a different family, showing vertical and circular geodesic segments.

  

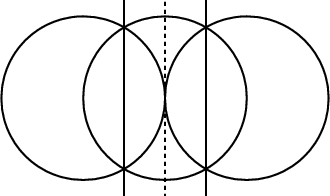
  Figure 6: The six circles related to the limit configuration for $\Gamma(N)$ with $N$ not divisible by $4$.

  

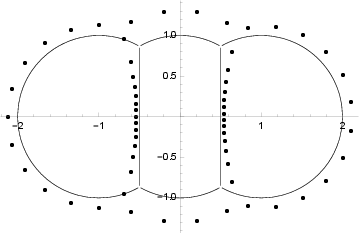
  Figure 7: Solutions of a finite truncation, superimposed on the limit configuration, illustrating convergence of zeros to geodesic arcs.

Implications and Future Directions

The results provide a precise geometric and arithmetic description of the zero sets of Eisenstein series for congruence groups, with explicit quantitative bounds and configurations. The geodesic clustering phenomenon is shown to be robust and universal across principal congruence groups, with the limit sets determined by group-theoretic and arithmetic invariants.

Potential future directions include:

• Extension to non-principal congruence groups and odd weights.
• Analysis of the arithmetic properties of norm modular forms and their $j$-invariants.
• Investigation of the fine-scale distribution and convergence speed of zeros for general modular forms.
• Study of the interplay between geodesic clustering and mass equidistribution for cusp forms.

Conclusion

This work establishes a detailed and explicit theory for the geometric clustering and arithmetic nature of zeros of Eisenstein series for congruence groups, revealing deep connections between modular form theory, analytic number theory, and hyperbolic geometry. The combination of analytic, algebraic, and geometric techniques yields a comprehensive picture of the limiting behavior and distribution of zeros, with strong implications for the structure of modular forms and their divisors on modular curves.