Part I: Tricks or Traps? A Deep Dive into RL for LLM Reasoning (2508.08221v1)

Abstract: Reinforcement learning for LLM reasoning has rapidly emerged as a prominent research area, marked by a significant surge in related studies on both algorithmic innovations and practical applications. Despite this progress, several critical challenges remain, including the absence of standardized guidelines for employing RL techniques and a fragmented understanding of their underlying mechanisms. Additionally, inconsistent experimental settings, variations in training data, and differences in model initialization have led to conflicting conclusions, obscuring the key characteristics of these techniques and creating confusion among practitioners when selecting appropriate techniques. This paper systematically reviews widely adopted RL techniques through rigorous reproductions and isolated evaluations within a unified open-source framework. We analyze the internal mechanisms, applicable scenarios, and core principles of each technique through fine-grained experiments, including datasets of varying difficulty, model sizes, and architectures. Based on these insights, we present clear guidelines for selecting RL techniques tailored to specific setups, and provide a reliable roadmap for practitioners navigating the RL for the LLM domain. Finally, we reveal that a minimalist combination of two techniques can unlock the learning capability of critic-free policies using vanilla PPO loss. The results demonstrate that our simple combination consistently improves performance, surpassing strategies like GRPO and DAPO.

• The paper introduces a minimalist RL approach using group-level mean normalization and token-level loss that consistently outperforms complex baselines.
• It employs rigorous experiments on Qwen3 models to compare normalization, clipping strategies, and loss aggregation, highlighting sensitivity to reward distributions.
• The study offers actionable guidelines that simplify engineering, improve reproducibility, and facilitate standardized RL for LLM reasoning.

Disentangling Reinforcement Learning Techniques for LLM Reasoning: Mechanistic Insights and Practical Guidelines

Introduction and Motivation

The application of reinforcement learning (RL) to LLM reasoning tasks has led to a proliferation of optimization techniques, each with distinct theoretical motivations and empirical claims. However, the lack of standardized guidelines and the prevalence of contradictory recommendations—often arising from inconsistent experimental setups, data distributions, and model initializations—have created substantial barriers to practical adoption. This work provides a systematic, mechanistic analysis of widely used RL techniques for LLM reasoning, focusing on normalization, clipping, filtering, and loss aggregation. Through rigorous, controlled experiments on the Qwen3 model family and open math reasoning datasets, the paper establishes actionable guidelines and demonstrates that a minimalist combination of two techniques—advantage normalization (group mean, batch std) and token-level loss—can consistently outperform more complex, technique-heavy baselines.

Figure 1: The proliferation of RL optimization techniques and the establishment of detailed application guidelines via mechanistic dissection, culminating in the introduction of a minimalist two-trick combination.

Experimental Setup and Baseline Analysis

The paper employs the ROLL framework for RL optimization, using PPO loss with REINFORCE-style advantage estimation. Experiments span Qwen3-4B and Qwen3-8B models, both base and aligned, and cover datasets of varying difficulty (SimpleRL-Zoo-Data, Deepmath). Evaluation is conducted on six math benchmarks, ensuring broad coverage of reasoning complexity.

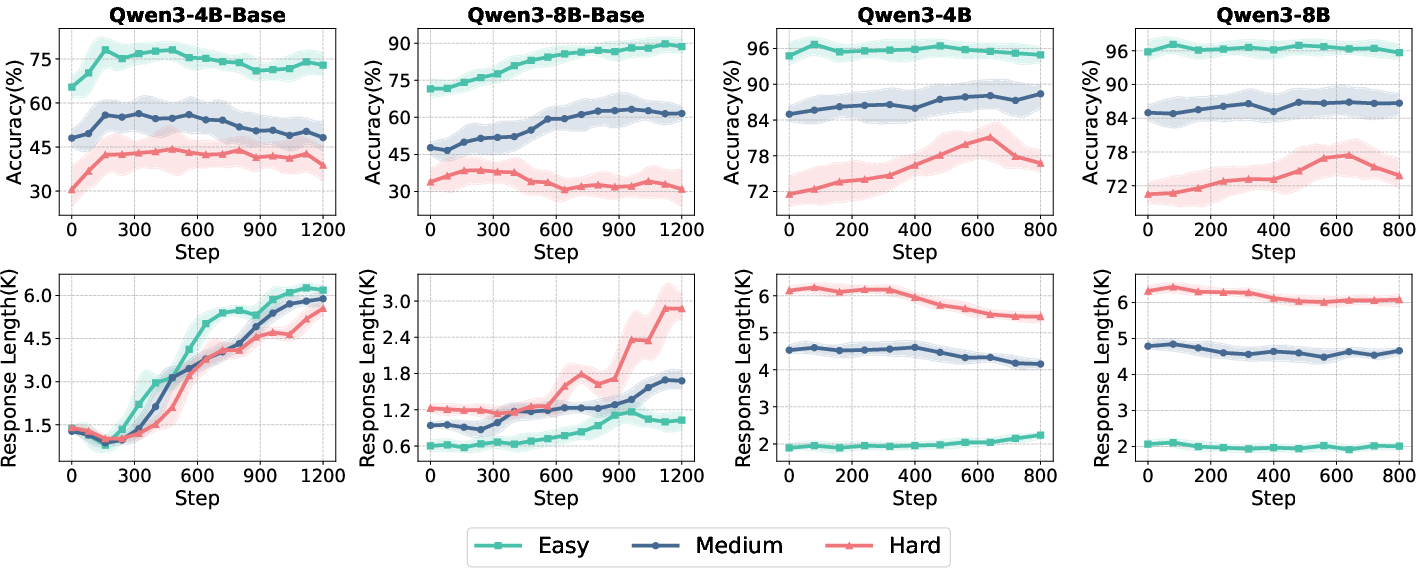
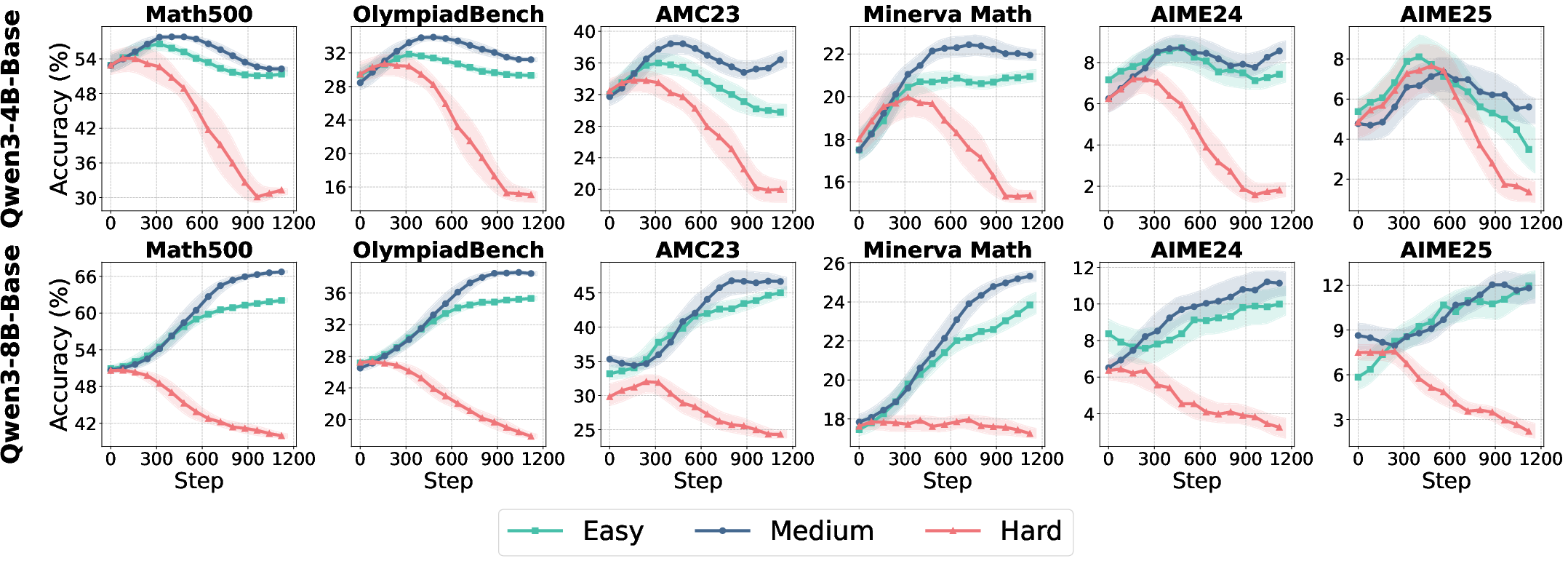
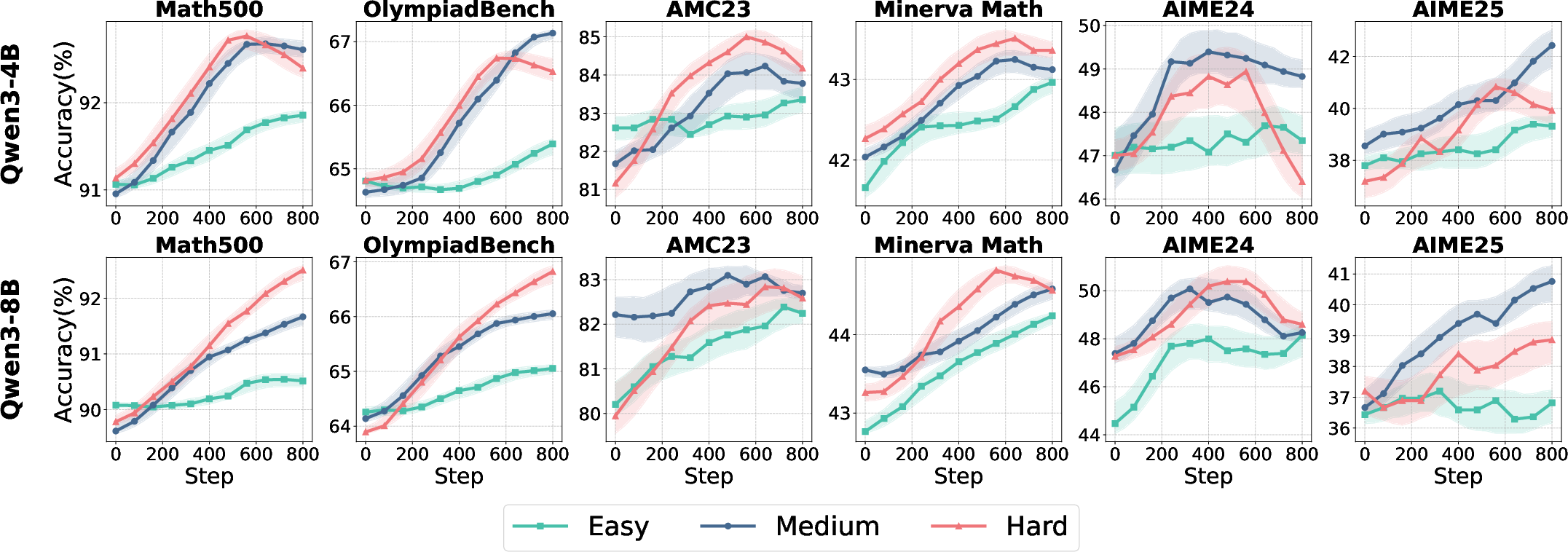
Figure 2: Training and test accuracy, as well as response length, for Qwen3-4B/8B (base and aligned) across data difficulty levels.

Key observations include:

• Aligned models exhibit higher initial accuracy and longer responses, but RL yields only marginal further gains.
• Data difficulty strongly modulates learning dynamics, with harder datasets inducing longer, more complex outputs and slower convergence.

Mechanistic Dissection of RL Techniques

Advantage Normalization

Advantage normalization is critical for variance reduction and stable policy optimization. The paper contrasts group-level normalization (per-prompt) with batch-level normalization (across all samples), revealing strong sensitivity to reward scale and distribution.

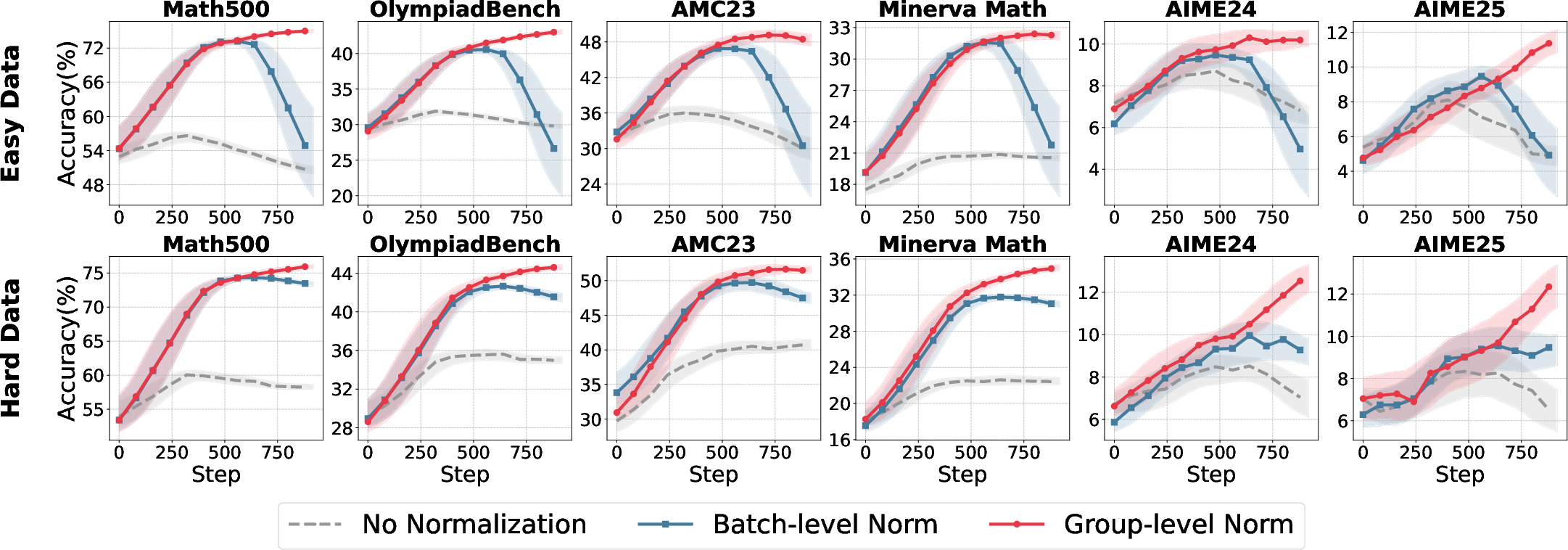
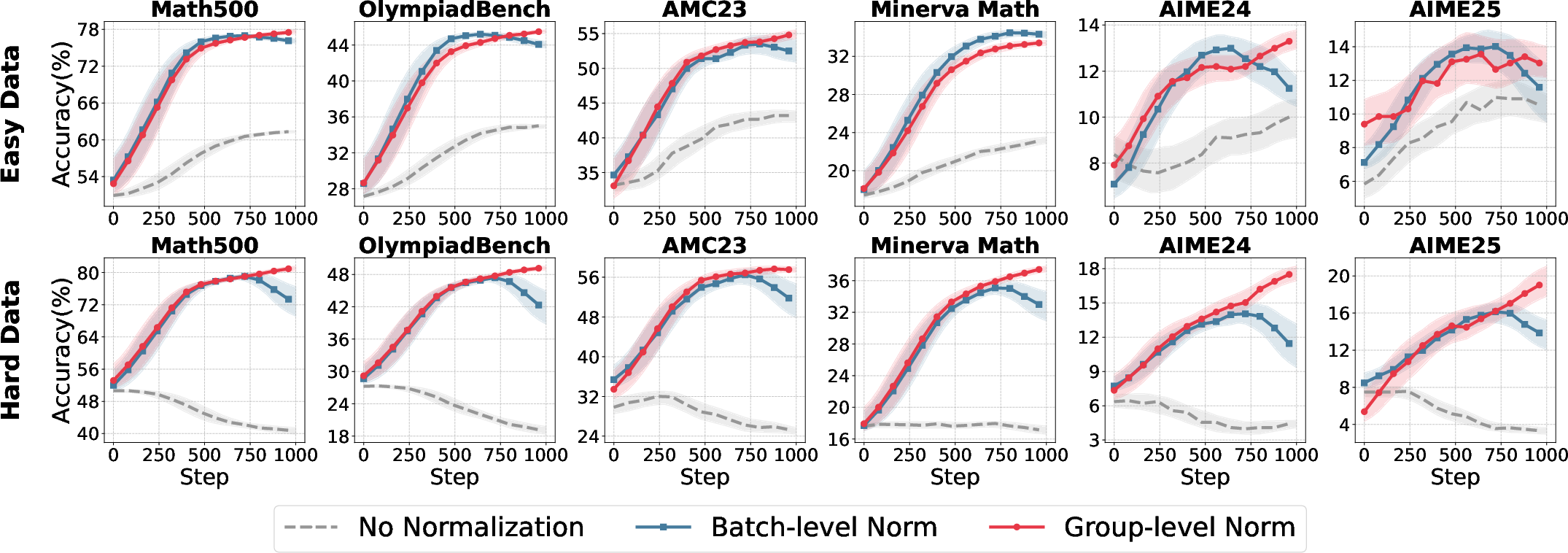
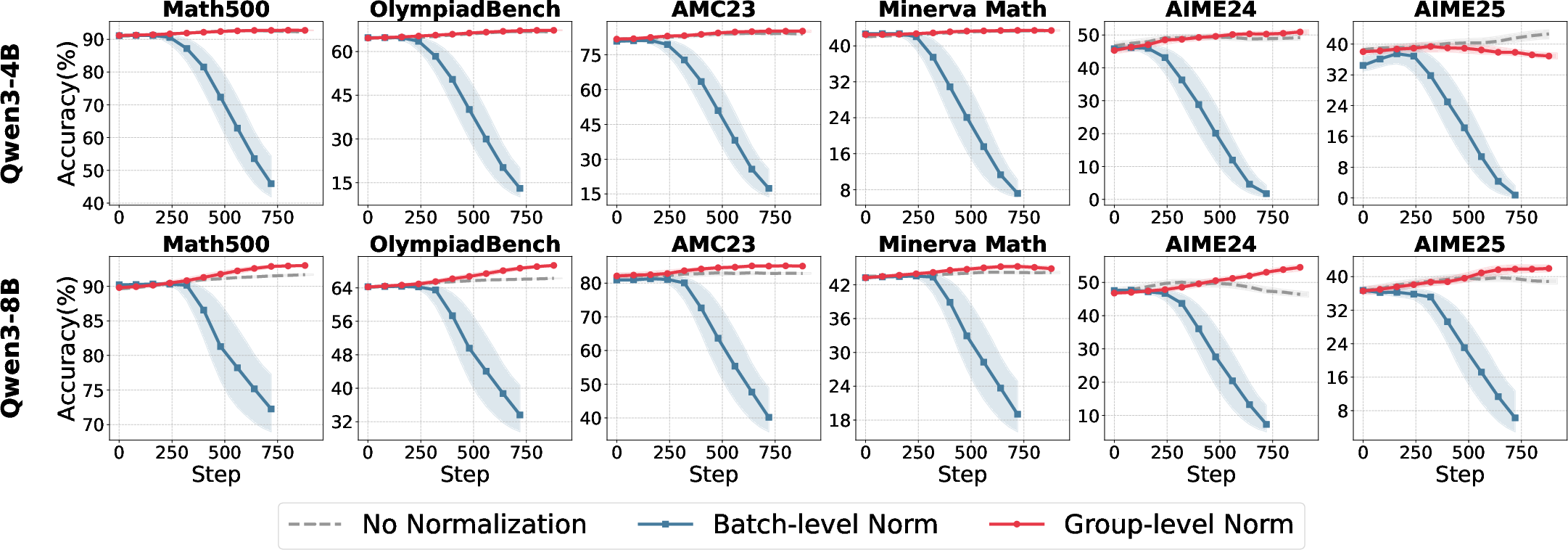
Figure 3: Accuracy over training iterations for Qwen3-4B/8B (base and aligned) under different normalization strategies.

• Group-level normalization is robust across reward settings, especially with binary rewards ($R \in \{0,1\}$).
• Batch-level normalization is unstable under skewed reward distributions but regains efficacy with larger reward scales ($R \in \{-1,1\}$).

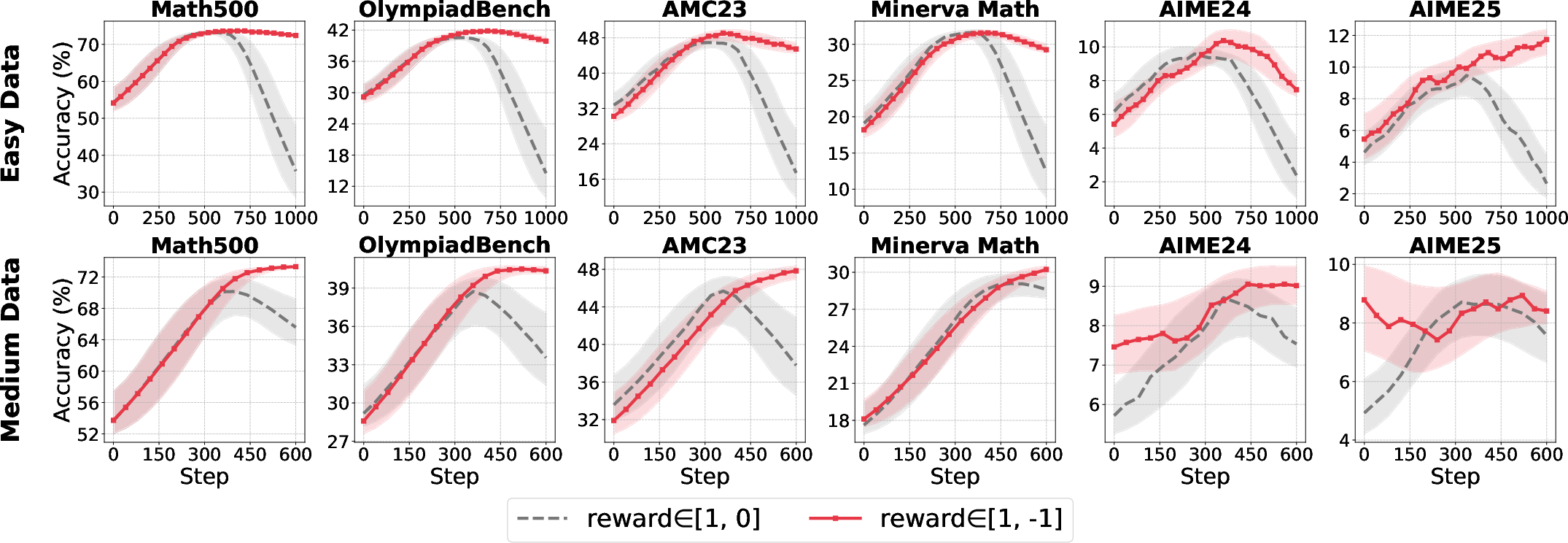
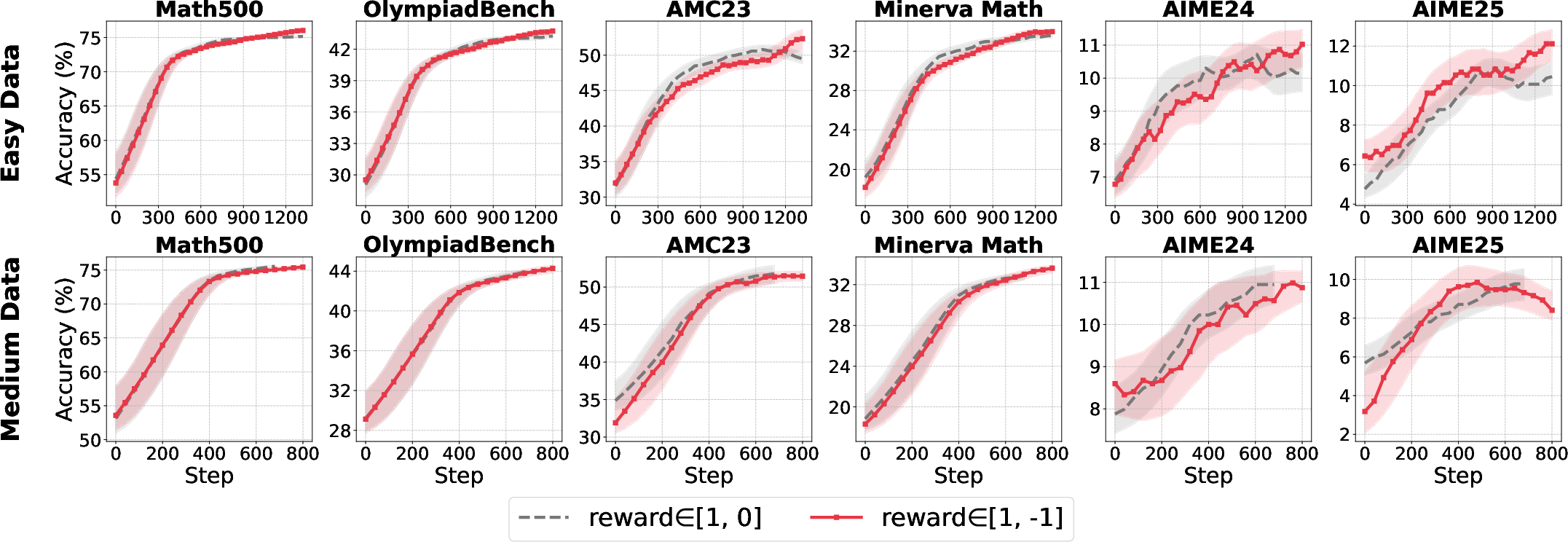
Figure 4: Impact of reward scale on batch- and group-level normalization for Qwen3-4B-Base.

Ablation on the standard deviation term demonstrates that, for highly concentrated reward distributions (e.g., easy datasets), removing the std prevents gradient explosion and stabilizes training.

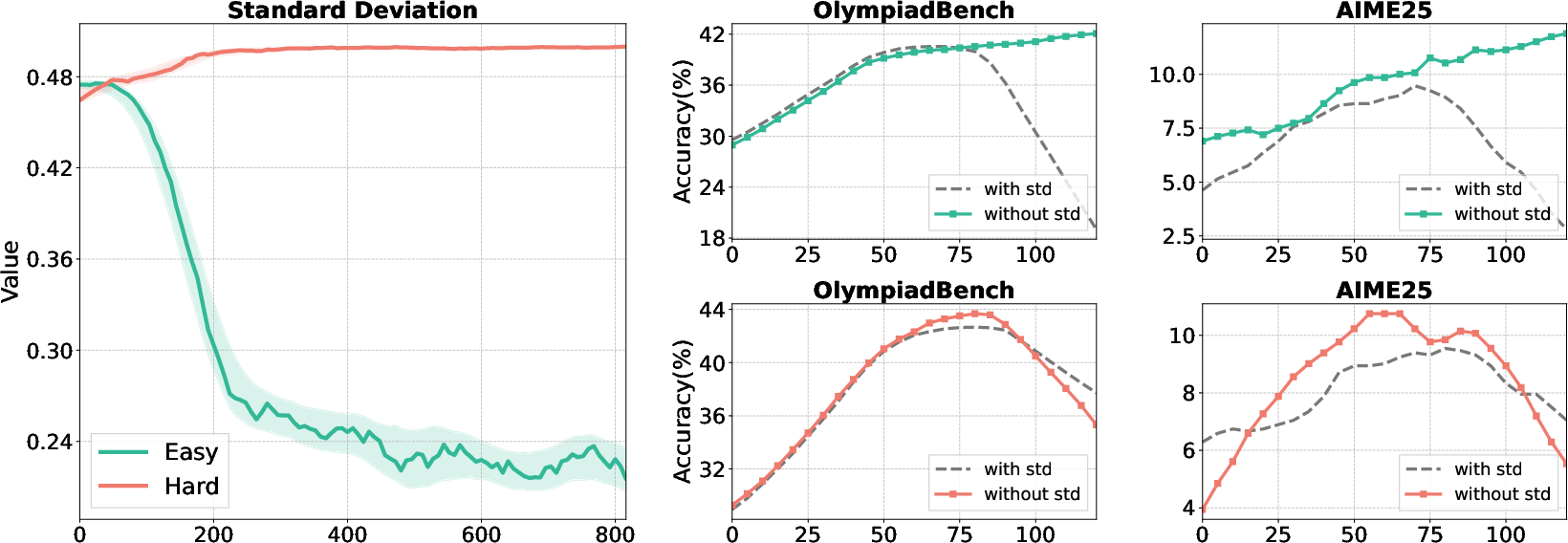
Figure 5: Left—std variation during training; Right—test accuracy before/after removing std from batch normalization.

Further, combining group-level mean with batch-level std yields the most robust normalization, effectively shaping sparse rewards and preventing overfitting to homogeneous reward signals.

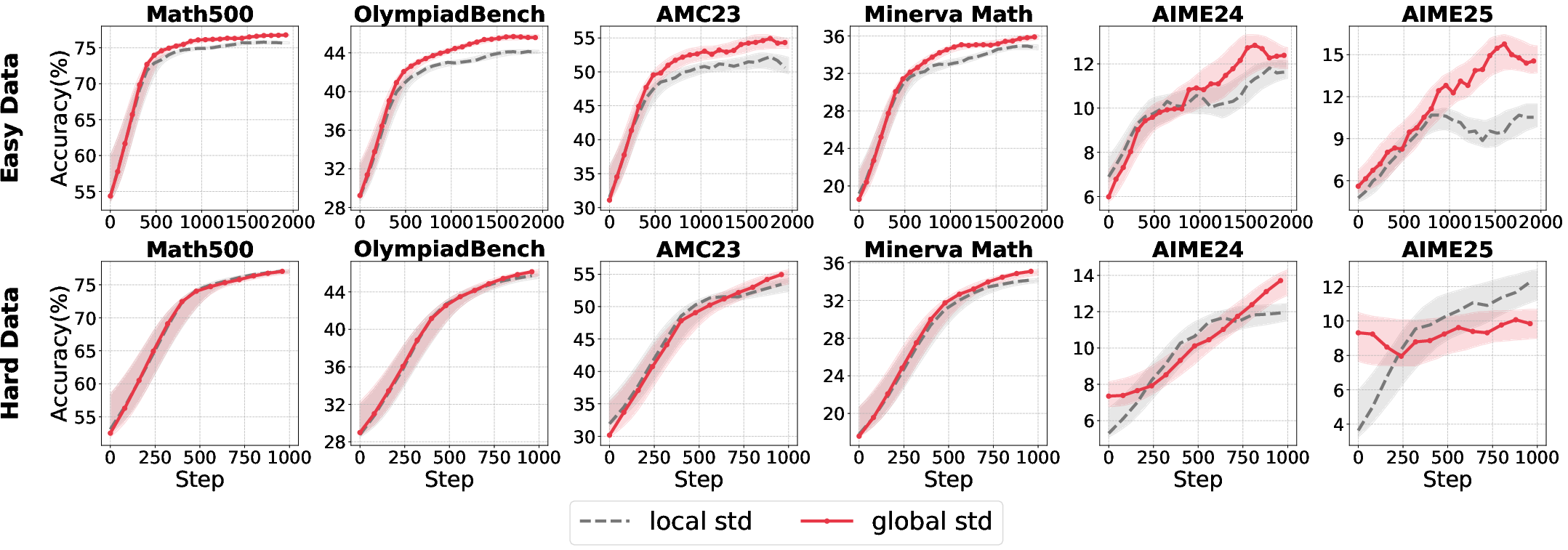
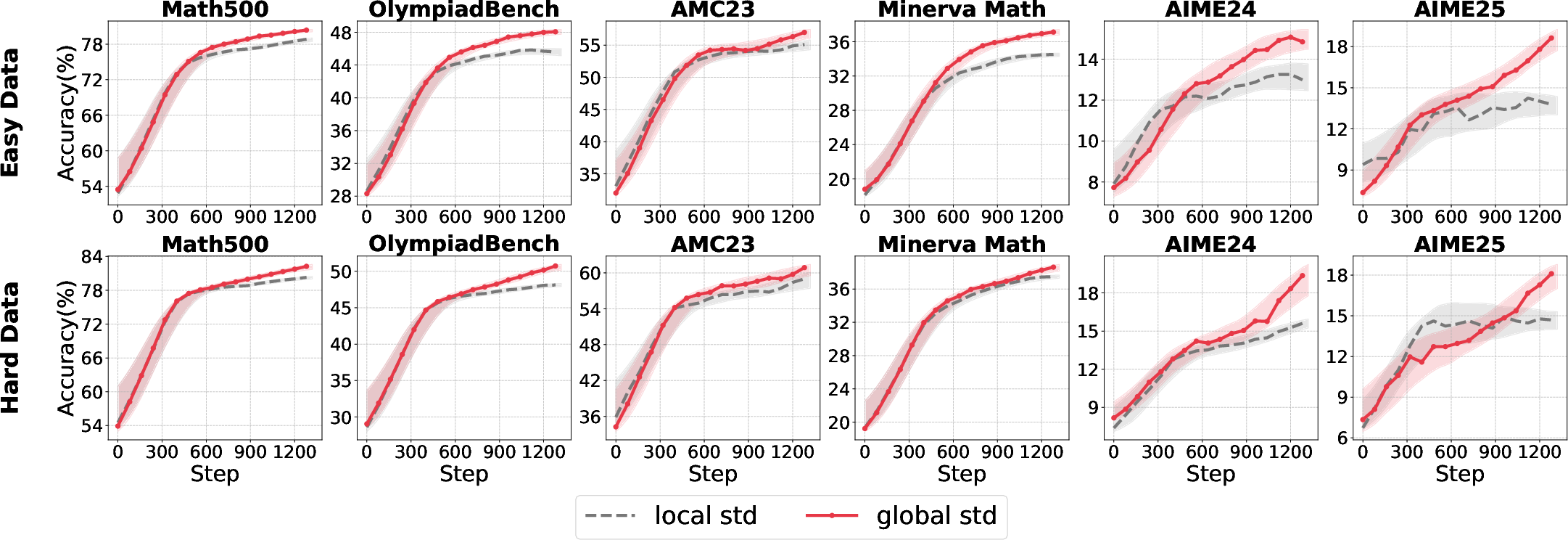
Figure 6: Comparative accuracy for different std calculation strategies on Qwen3-4B/8B-Base.

Clipping Strategies: Clip-Higher

The standard PPO clipping mechanism can induce entropy collapse, especially in LLMs, by over-suppressing low-probability tokens. The Clip-Higher variant relaxes the upper bound, promoting exploration and mitigating entropy loss.

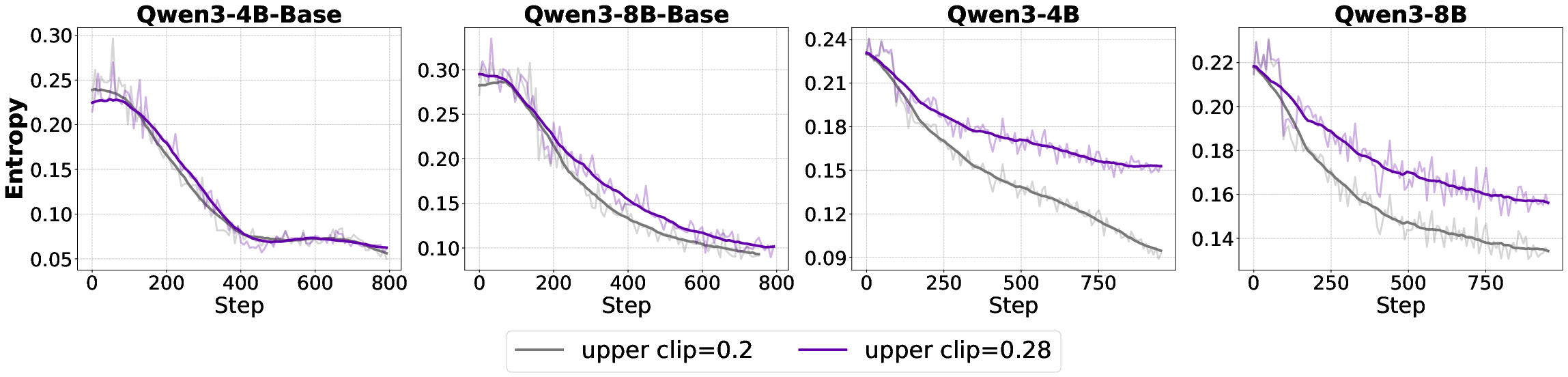
Figure 7: Entropy comparison across models with varying clip upper bounds; higher bounds slow entropy collapse in aligned models.

Empirical results show:

• For base models, increasing the clip upper bound has negligible or negative effects.
• For aligned models, higher upper bounds consistently improve exploration and downstream accuracy.

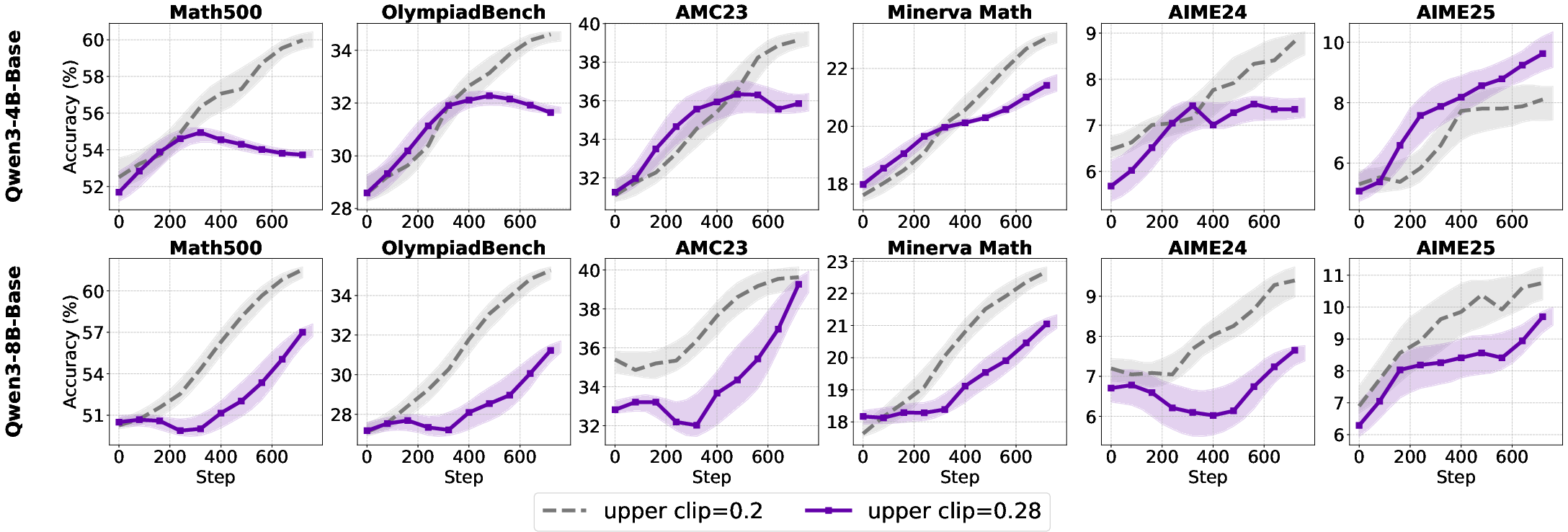
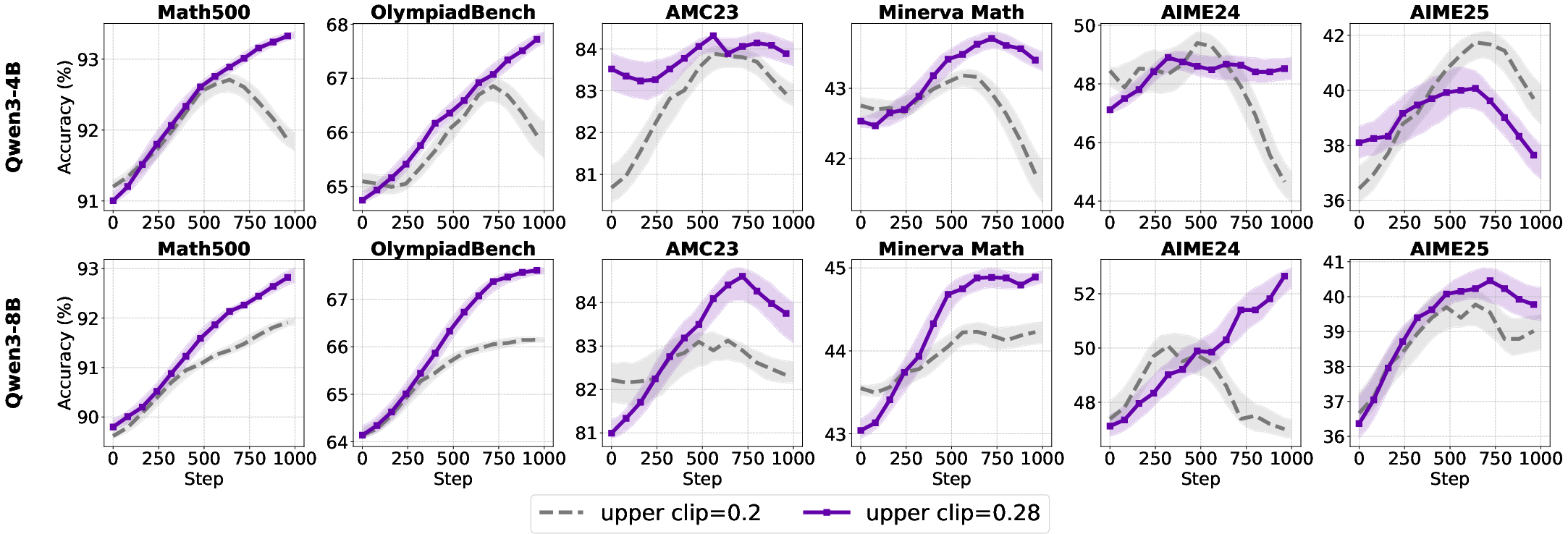
Figure 8: Test accuracy of base and aligned models under different clip upper bounds.

Token-level analysis reveals that stricter clipping disproportionately suppresses discourse connectives, limiting reasoning diversity, while higher bounds shift clipping to function words, enabling more flexible reasoning structures.

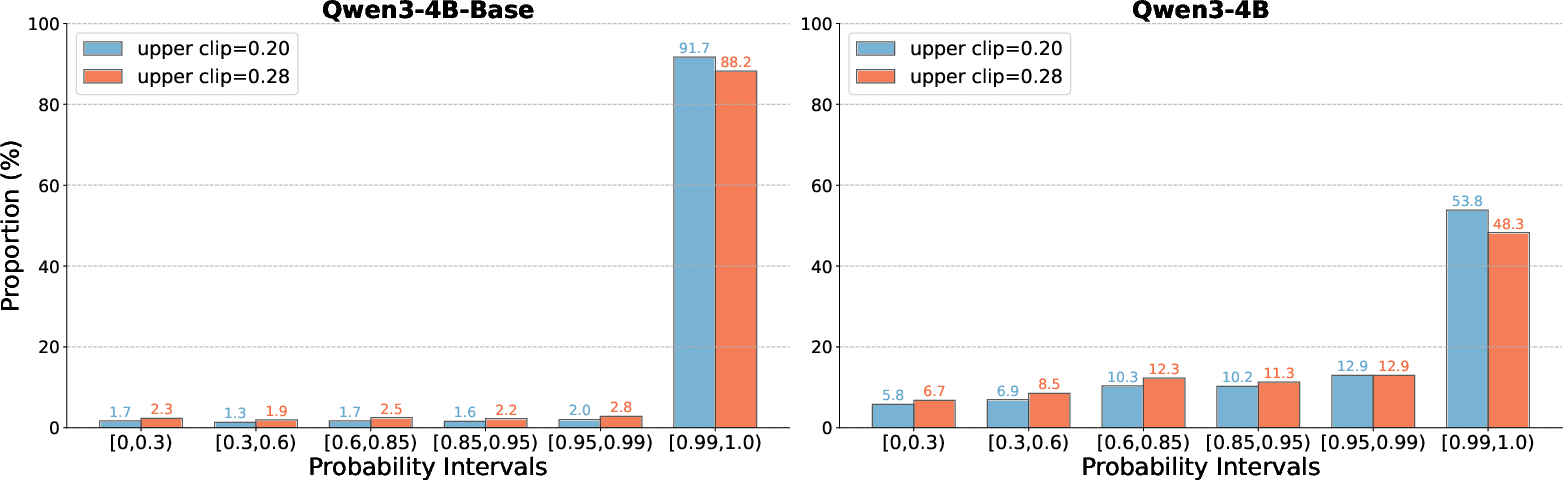
Figure 9: Token probability distributions for Qwen3-4B-Base and Qwen3-4B under different clip upper bounds.

Figure 10: Case paper of clipping effects on token selection and frequency.

A scaling law is observed for small models: performance improves monotonically with increased clip upper bound, peaking at 0.32, whereas larger models saturate at 0.28.

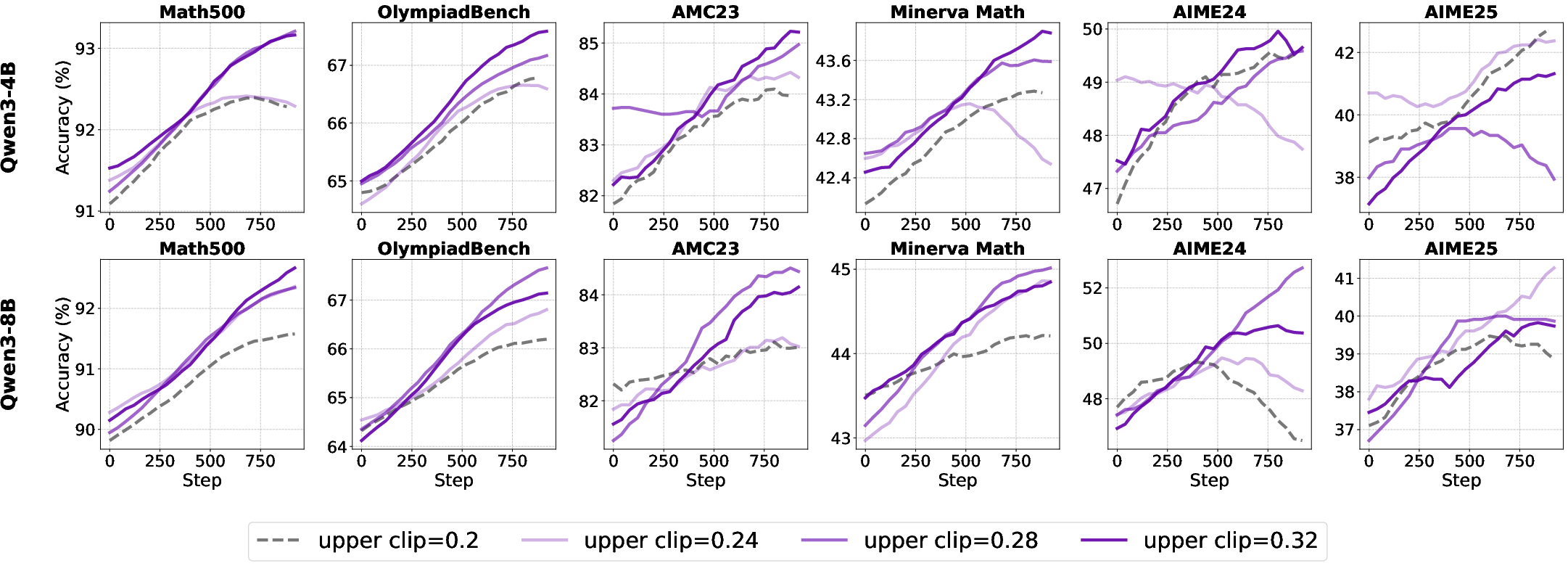
Figure 11: Test accuracy of aligned models with various clip upper bounds.

Loss Aggregation Granularity

The choice between sequence-level and token-level loss aggregation has significant implications for optimization bias and learning efficiency.

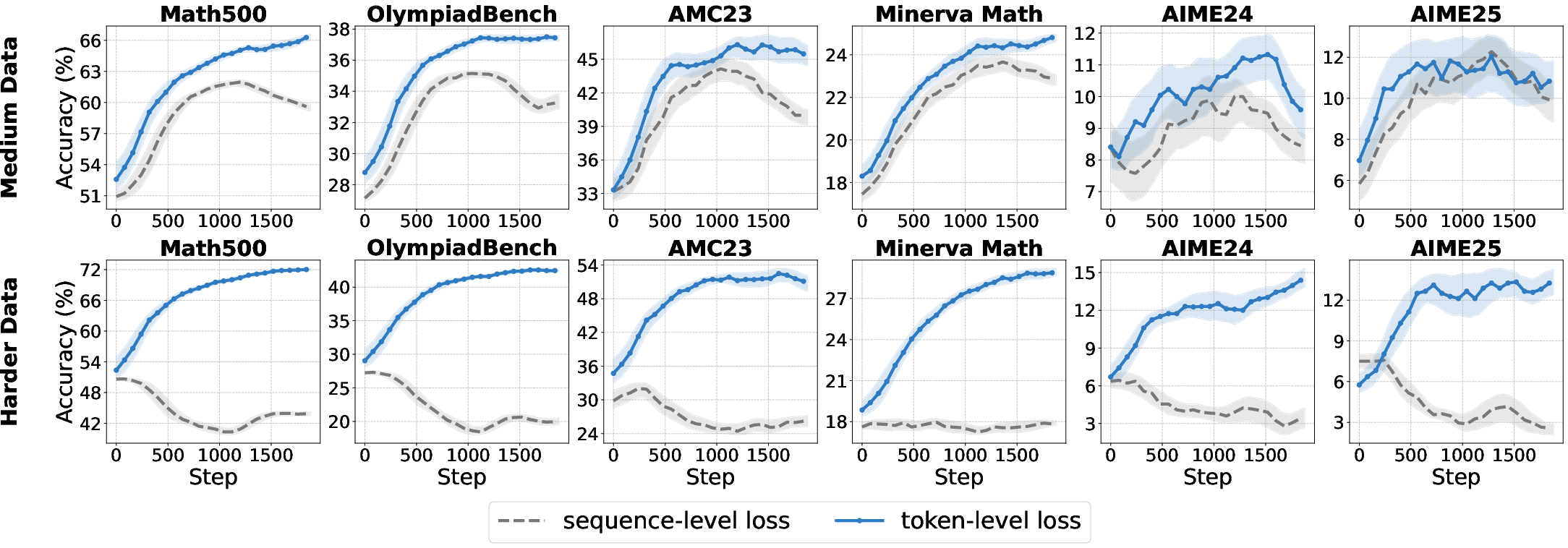
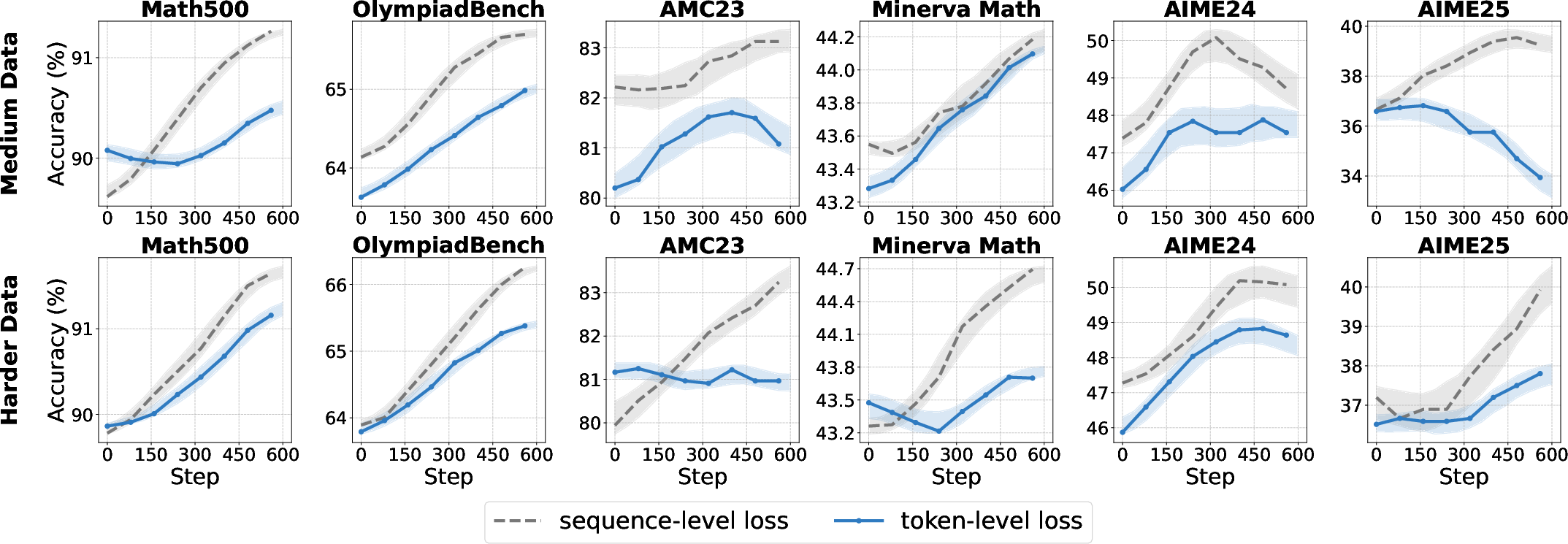
Figure 12: Accuracy comparison between sequence-level and token-level loss for Qwen3-8B (base and aligned) on easy and hard datasets.

• Token-level loss is superior for base models, ensuring equal gradient contribution per token and improving convergence on complex data.
• Sequence-level loss is preferable for aligned models, preserving output structure and stability.

Overlong Filtering

Overlong filtering masks the reward signal for excessively long responses, preventing penalization of truncated but otherwise correct reasoning chains.

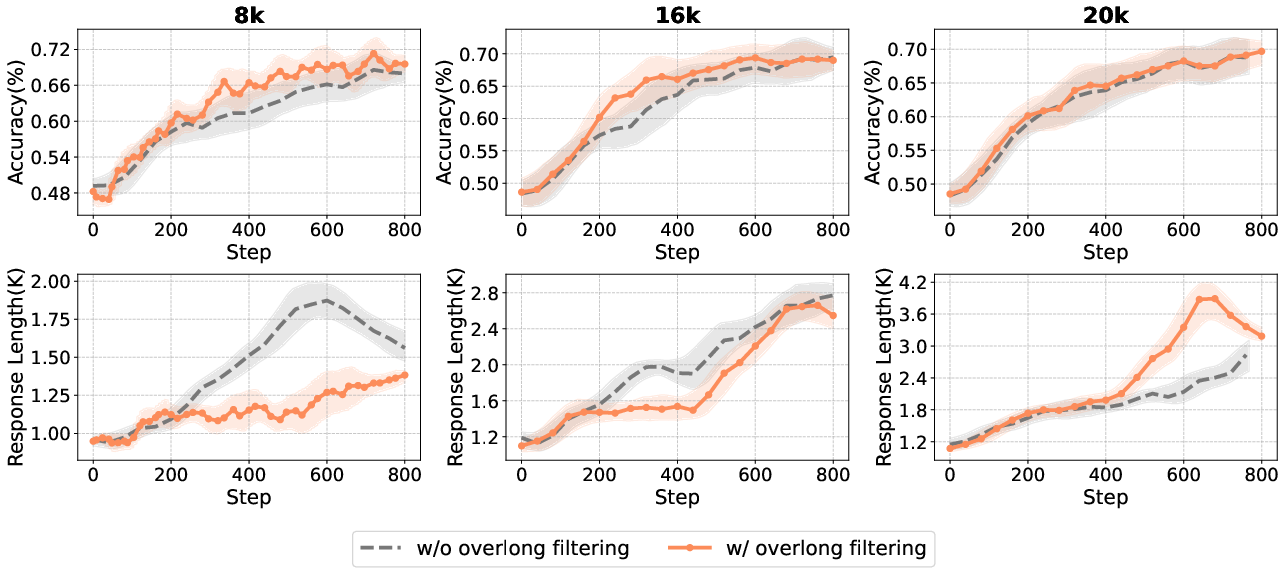
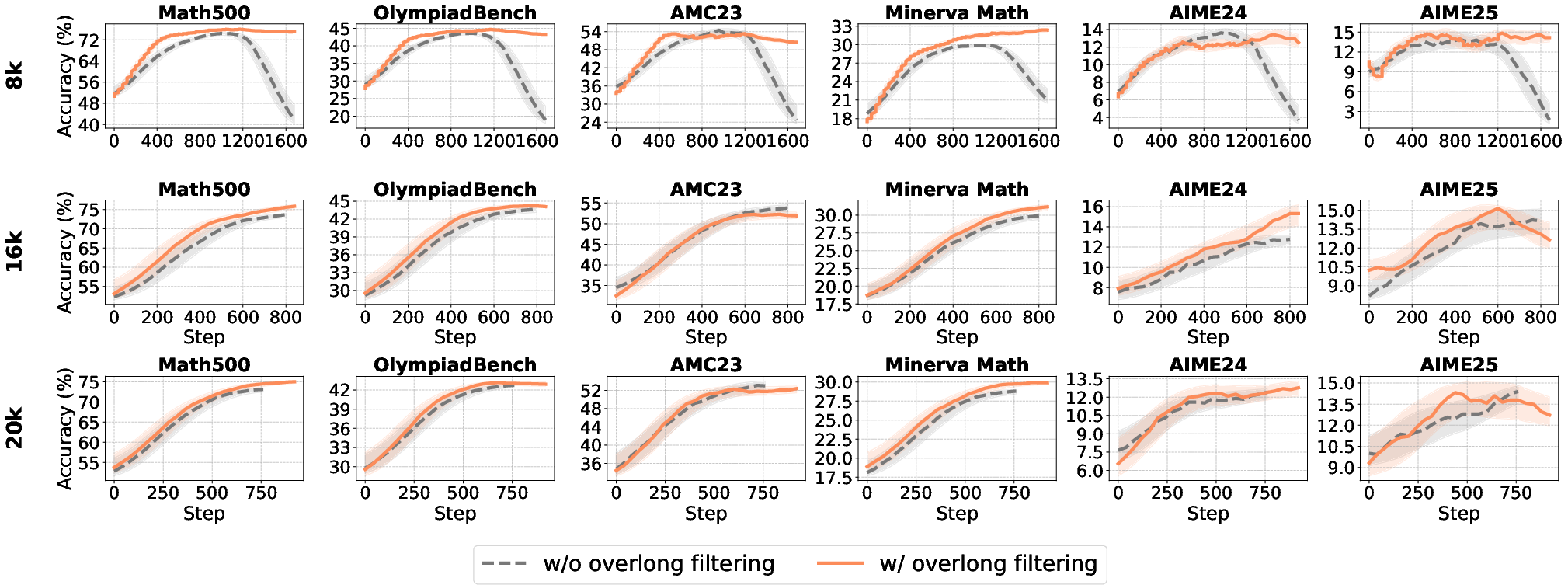
Figure 13: Training accuracy and response length for Qwen3-8B-Base under different max generation lengths and overlong filtering.

• Overlong filtering is effective for short/medium-length reasoning tasks but offers limited benefit for long-tail tasks.
• High max length settings primarily filter degenerate, repetitive outputs, while lower thresholds encourage concise, well-terminated responses.

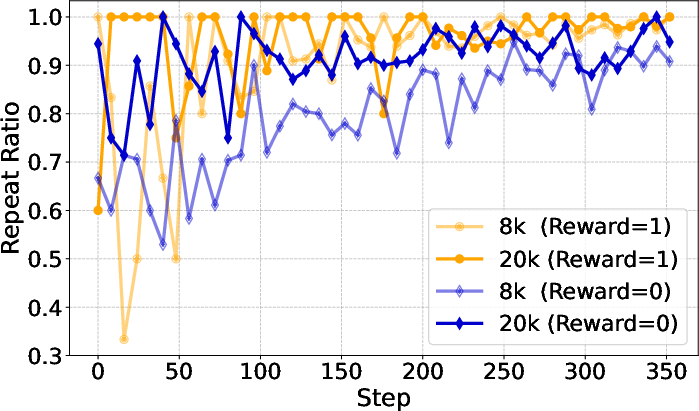
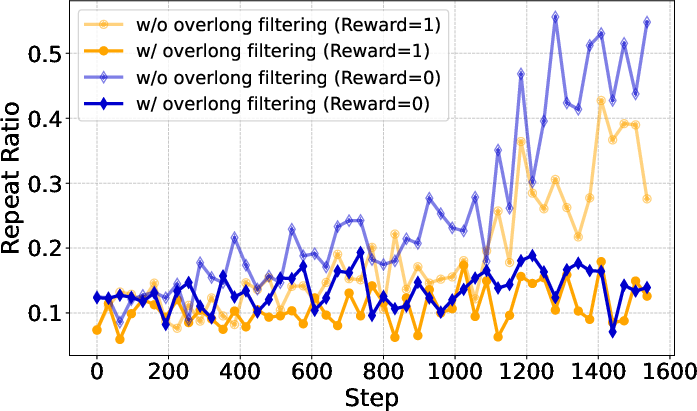
Figure 14: Repeat ratio analysis for correct/incorrect generations and effect of overlong filtering on truncated samples.

Minimalist Recipe: Lite PPO

Synthesizing the mechanistic findings, the paper proposes Lite PPO: a critic-free PPO variant using group-level mean and batch-level std for advantage normalization, combined with token-level loss aggregation. This minimalist approach consistently outperforms more complex baselines such as GRPO and DAPO across Qwen3-4B/8B-Base models and diverse data regimes.

Figure 15: Test accuracy of non-aligned models trained via Lite PPO, GRPO, and DAPO.

The strong performance of Lite PPO is attributed to its robust handling of sparse, skewed rewards and its avoidance of overfitting to homogeneous or degenerate samples.

Implications and Future Directions

This work provides a principled foundation for RL4LLM technique selection, challenging the prevailing trend of over-engineered pipelines. The empirical evidence that a two-trick combination can outperform technique-heavy baselines has significant implications for both research and deployment: it reduces engineering overhead, improves reproducibility, and facilitates broader adoption of RL for LLM reasoning.

The findings also highlight the need for model-family-specific analysis, as conclusions may not generalize across architectures with different pretraining or alignment regimes. The authors advocate for increased transparency in model and training details to enable more rigorous, cross-family benchmarking.

Future research directions include:

• Extending the unified ROLL framework to support modular benchmarking of diverse RL algorithms.
• Investigating the transferability of the minimalist recipe to other LLM families and reasoning domains.
• Exploring further simplification and theoretical unification of RL4LLM techniques.

Conclusion

This paper systematically demystifies the practical and theoretical underpinnings of RL techniques for LLM reasoning, providing clear, empirically validated guidelines. The demonstration that a minimalist combination of group-level mean, batch-level std normalization, and token-level loss suffices for robust policy optimization in critic-free PPO settings challenges the necessity of complex, ad hoc pipelines. These insights are poised to inform both future research and industrial practice, accelerating progress toward standardized, efficient, and effective RL4LLM methodologies.