Sublattice polarization from destructive interference on common lattices (2406.02671v2)

Abstract: We show that sublattice-polarized states (SLPSs) appear ubiquitously on the common lattices. We first establish the destructive-interference (DI) scenario for the SLPSs, which is systematized by a point-group-symmetry interpretation. The examples on common one-, two-, and three-dimensional lattices are then demonstrated. We also deduce the symmetry-protected robustness of SLPSs against further-neighbor hoppings. Moreover, the DI scenario can be generalized to the multi-SLP. The important effects on interaction-driven phases are studied by Hartree-Fock analysis.

• The paper demonstrates that sublattice-polarized states emerge from destructive interference in various lattice structures, validated using a tight-binding framework.
• Analysis across 1D, 2D, and 3D lattices shows that symmetry and nearest-neighbor connectivity are critical for SLPS formation and robustness.
• Hartree-Fock studies reveal SLPSs significantly alter interaction-driven phases, influencing ferromagnetism and charge-density modulations at weak coupling.

Sublattice Polarization from Destructive Interference on Common Lattices

This paper introduces a framework for understanding the occurrence and robustness of sublattice-polarized states (SLPSs) on various lattice structures, attributed to a mechanism of destructive interference (DI). The approach systematically explores these states across several lattice dimensions and types, providing a cohesive analysis reinforced by point-group-symmetry interpretations.

Fundamental Mechanism and Point-Group Symmetry

SLPSs are shown to arise from DI between sublattices. This interference effectively prevents the propagation of wavefunctions across sublattices, leading to localized states. The tight-binding model illustrates this phenomenon mathematically as:

$$H=-\sum_{ii'}\sum_{\tau\tau'}t_{ii'\tau\tau'}c_{i\tau}^\dagger c_{i'\tau'}$$

where $c_{i\tau}^{(\dagger)}$ represents fermionic operators, and $t_{ii'\tau\tau'}$ are hopping terms. A critical insight is that SLPSs manifest generally in lattices where the nearest-neighbor connections are $N^{\tau\tau'}_1 \geq 2$. The occurrence of SLPSs aligns with nontrivial irreps of point-group symmetry, specifically through the role of these groups in defining wavefunction harmonics at a site $i'\tau'$.

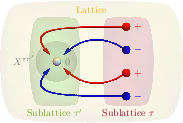
Figure 1: DI scenario illustrating SLPS prevention of wavefunction spreading under nearest-neighbor hoppings.

Examples Across Lattice Dimensions

1D Lattices

In 1D, lattices like the zigzag lattice with $N^{01}_1=2$ demonstrate SLPSs due to wavefunction staggering. The SLPS energy in these systems often respects a staggered pattern resembling a lattice's edge, shown in band structures as nodal points or lines.

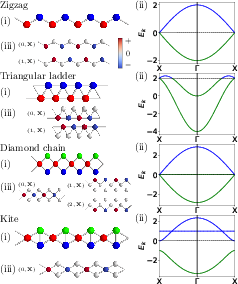
Figure 2: Examples of 1D lattices showing SLPS configurations and energy bands.

2D Lattices

SLPS occurrence in 2D lattices includes well-known formations like the honeycomb and kagome lattices. In systems with triangular Bravais lattices, symmetry and connection integer dictate SLPS locations, such as at BZ corners or edges.

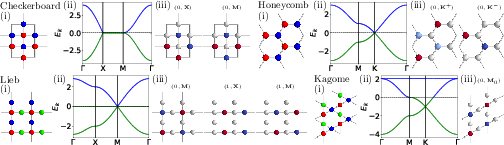
Figure 3: 2D lattice examples where SLPSs emerge at high-symmetry BZ points, depicted by lattice diagrams and band structures.

3D Lattices

3D analogs extend SLPS conclusions from 2D to structures like the diamond lattice. Here, the highly symmetrical BCC and FCC structures showcase linked SLPS presence at specific BZ points, influenced heavily by high-dimensional symmetry arguments.

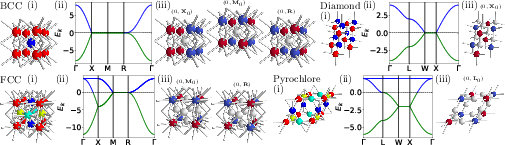
Figure 4: SLPS examples in 3D lattices, highlighting the influence of high-dimensional symmetry on state robustness.

Robustness and Interaction with Further-Neighbor Hoppings

SLPSs exhibit symmetry-protected resilience against further-neighbor uniform hoppings. These features stem from sustained DI across higher-order connections, maintaining SLPS eigenstates even when new hopping terms are introduced.

Exceptional cases arise when the nearest-neighbor connection index $N^{\tau\tau'}_1=0$, where neighbor effects can compromise SLPS presence. However, as affirmed in several lattices studied, symmetry considerations largely uphold DI, maintaining SLPS characteristics.

Hartree-Fock Analysis and Interaction-Driven Phases

The Hartree-Fock framework is employed to analyze how SLPSs affect interaction-driven phases. It reveals that SLP effects can significantly alter Fermi surface behavior, primarily promoting intra-unit-cell orders such as ferromagnetism and charge-density modulations. This influence is notably robust at weak coupling, where zero SLPS energy is considered.

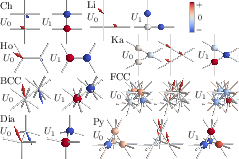
Figure 5: Representative interaction-driven ground states on various lattices, showing charge and spin ordering due to SLPS impact.

Conclusion

The paper fundamentally redefines SLPS understanding through DI mechanisms, applicable to a variety of lattice structures prevalent in condensed matter physics. The robustness of SLPSs under different hopping conditions and their significant impact on interaction-driven phases underline their potential for discovery in quantum materials and applications in quantum technology.

These insights extend the theoretical landscape for future lattice model explorations, suggesting pathways for experimental verification and practical implementation in synthetic matter systems. The DI framework provides a robust foundation for exploring symmetry-enhanced quantum states across physical and engineered systems alike.