Understanding Token Probability Encoding in Output Embeddings (2406.01468v2)

Abstract: In this paper, we investigate the output token probability information in the output embedding of LLMs. We find an approximate common log-linear encoding of output token probabilities within the output embedding vectors and empirically demonstrate that it is accurate and sparse. As a causality examination, we steer the encoding in output embedding to modify the output probability distribution accurately. Moreover, the sparsity we find in output probability encoding suggests that a large number of dimensions in the output embedding do not contribute to causal language modeling. Therefore, we attempt to delete the output-unrelated dimensions and find more than 30% of the dimensions can be deleted without significant movement in output distribution and sequence generation. Additionally, in the pre-training dynamics of LLMs, we find that the output embeddings capture the corpus token frequency information in early steps, even before an obvious convergence of parameters starts.

• The paper presents a log-linear encoding method that accurately represents output token probabilities in large language models through sparse embeddings.
• It utilizes multiple linear regression to derive empirical constants and validate robust log-linear relationships in models like GPT-2 and GPT-J.
• The work demonstrates efficient editing and pruning, showing that over 30% of embedding dimensions can be removed without degrading model performance.

Understanding Token Probability Encoding in Output Embeddings

This essay explores the paper titled "Understanding Token Probability Encoding in Output Embeddings," which explores the intricate mechanisms of how token probabilities are encoded within the output embeddings of LMs. The paper highlights the sparse and accurate log-linear encoding of output token probabilities, demonstrating innovative ways to manipulate these probabilities and reduce model complexity.

Core Findings and Theoretical Framework

The paper presents an approximate log-linear encoding for output token probabilities, revealing that in large-output-space LMs, such encoding is not only feasible but also precise and sparse. This is evident in scenarios where output dimensions are large, and logits are concentrated, aligning closely with the properties of LLMs such as GPT-2 and GPT-J.

Mathematical Derivation

The paper derives that the output probabilities $P_\theta(w|x)$ can be expressed log-linearly with respect to the output embeddings $E^{(o)}$. Using a $\mathrm{softmax}$ function in the LM head, the probability distribution for token $w$ at embedding $E^{(o)}$ is approximated as:

$$-\log \alpha_{w,\mathcal{D}, \theta} \approx A_{\mathcal{D}} \cdot E_w^{(o)} + B_{\mathcal{D}}.$$

Here, $A_{\mathcal{D}}$ and $B_{\mathcal{D}}$ are empirical constants derived through multiple linear regression (MLR). This theoretical underpinning is validated by empirical evidence showing robust log-linear relationships across various LMs like GPT-2 and GPT-J.

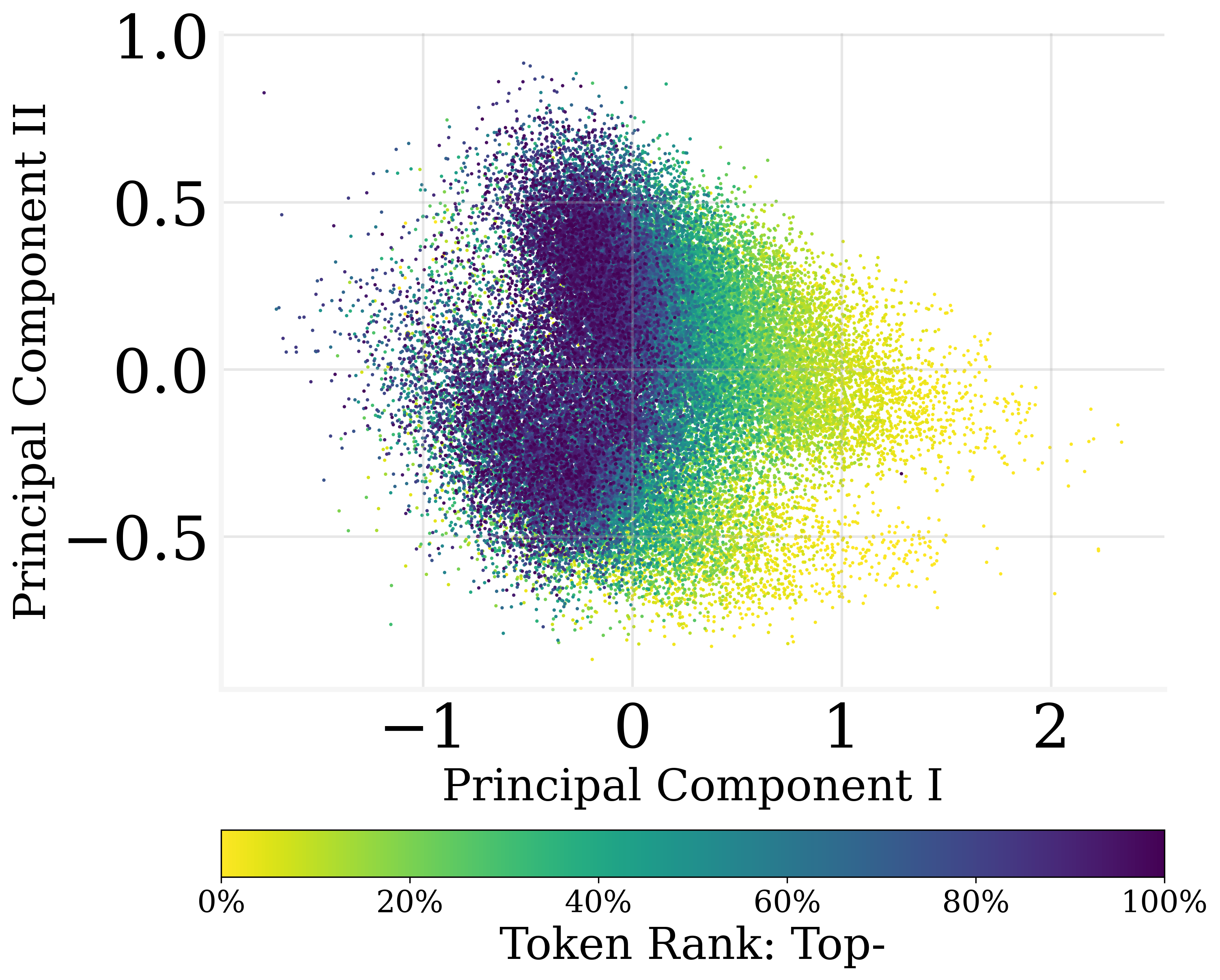
Figure 1: The PCA result of the output embedding parameters of GPT2. Colors refer to the ranking percentile of the averaged output token probability. Output embeddings encode the probabilities linearly.

Implementation of Token Probability Editing

To demonstrate the utility of the log-linear encoding, the authors propose an algorithm to edit token probabilities by altering specific dimensions in the output embeddings.

Editing Algorithm

The algorithm, grounded in MLR results, applies a vectorized approach to modify embedding dimensions based on their correlation strength with token probabilities. The editing process involves:

1. Calculating averaged token probabilities over a detection dataset.
2. Performing MLR to ascertain the contribution of each dimension.
3. Allocating editing weights and updating embeddings to achieve desired probability scales.

This method enables precise adjustments of output probabilities, allowing for controlled scaling up to 20x without significant disruption of the model's prediction process.

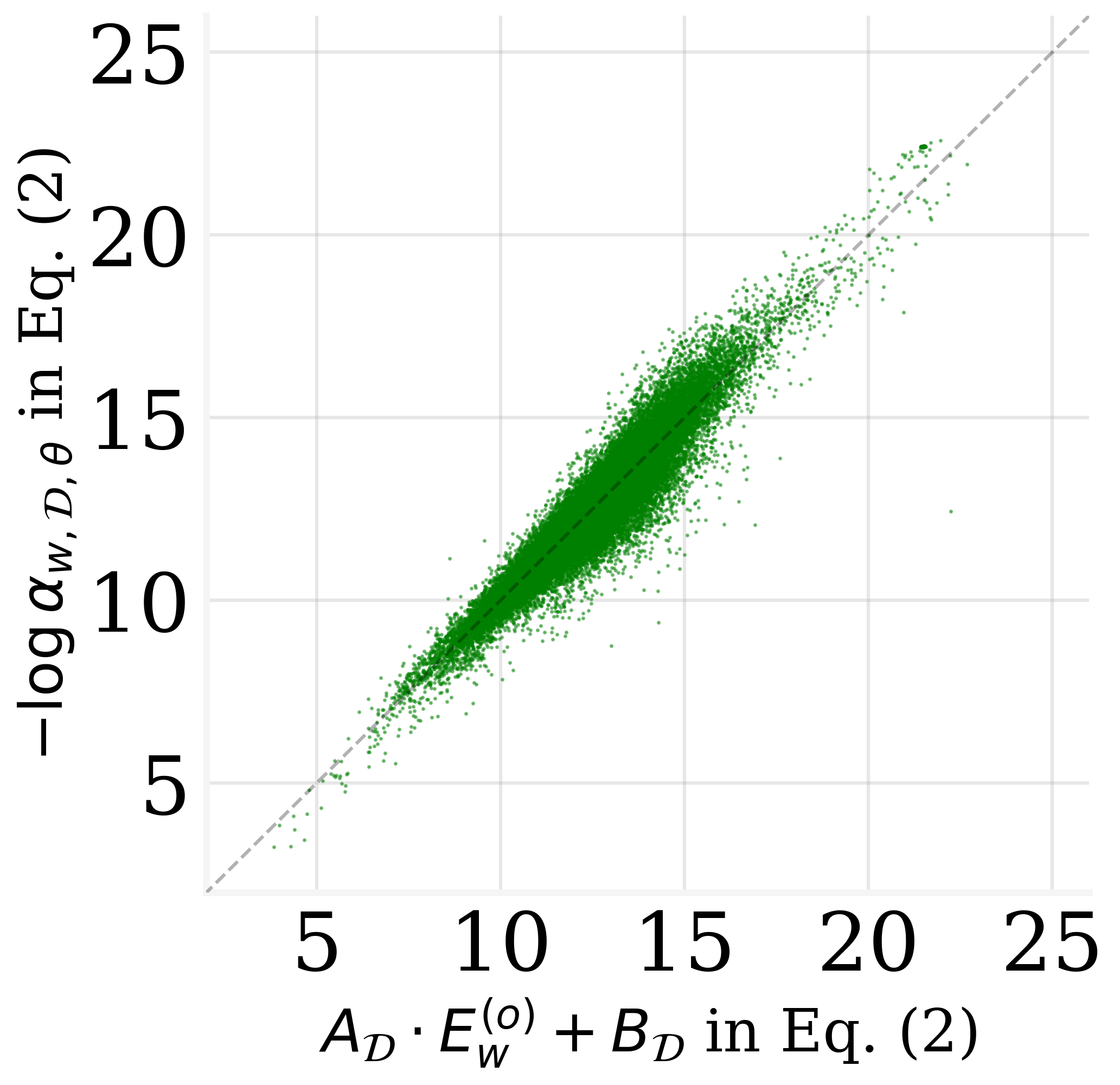
Figure 2: The MLR results on GPT2 and GPT-J.

Dimensionality Reduction in Output Embeddings

The paper finds that more than 30% of the output embedding dimensions can be pruned without degrading model performance significantly. This revelation stems from the observation that many dimensions exhibit weak correlations with output probabilities.

Methodology and Results

Utilizing MLR slope metrics, dimensions are ranked by their contribution to output encoding. The least impactful dimensions can be zeroed out, facilitating parameter reduction and contributing to model sparsity.

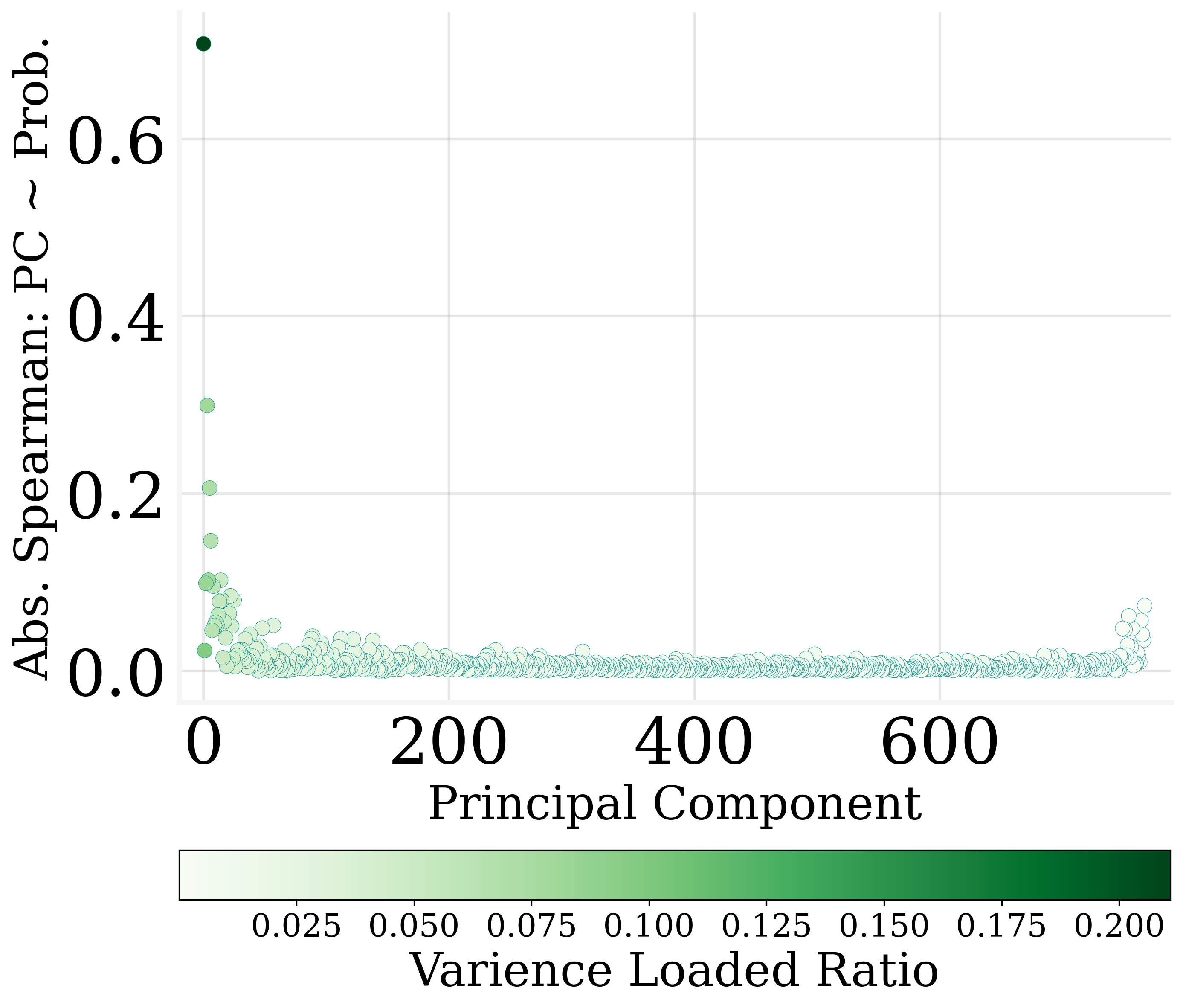
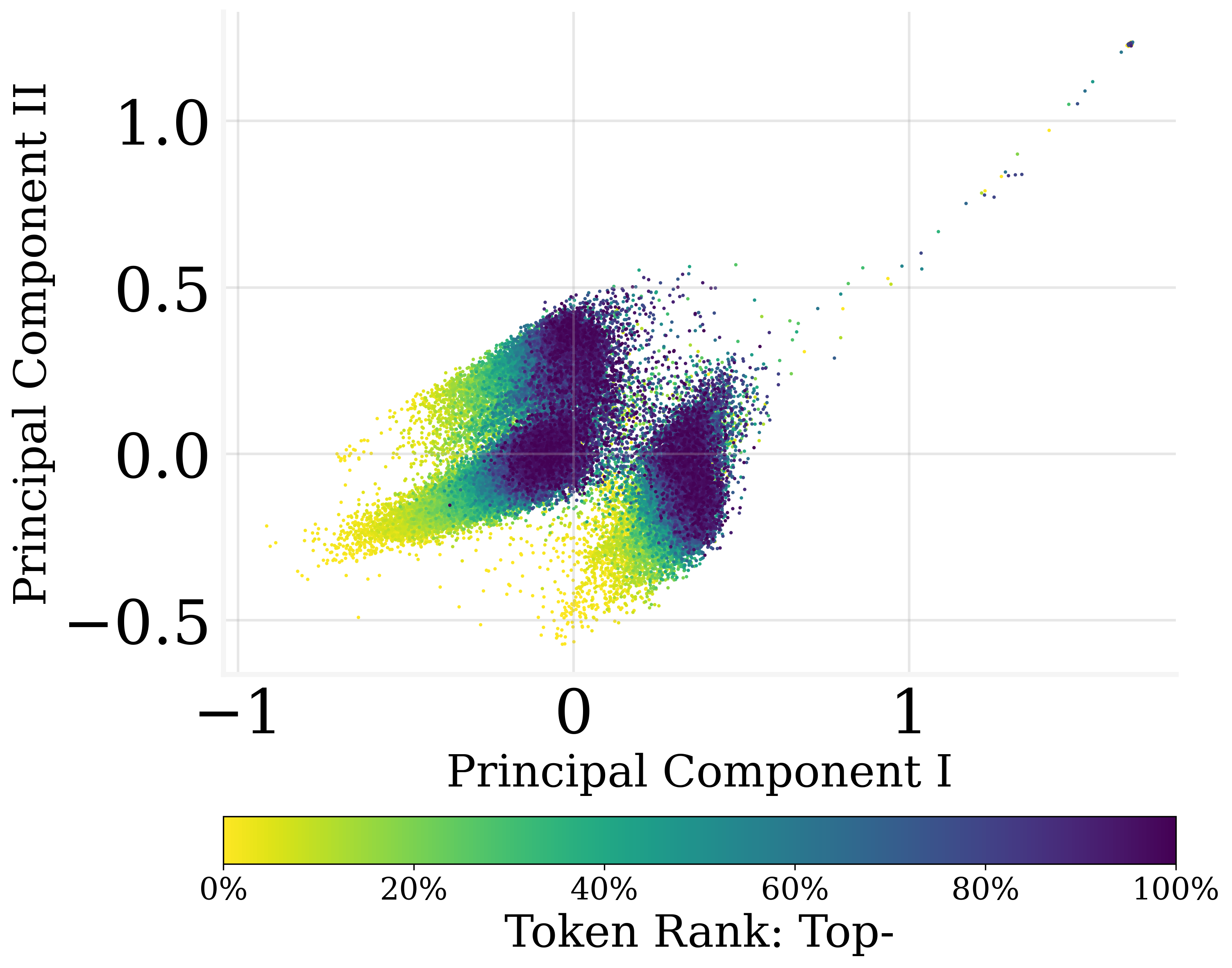
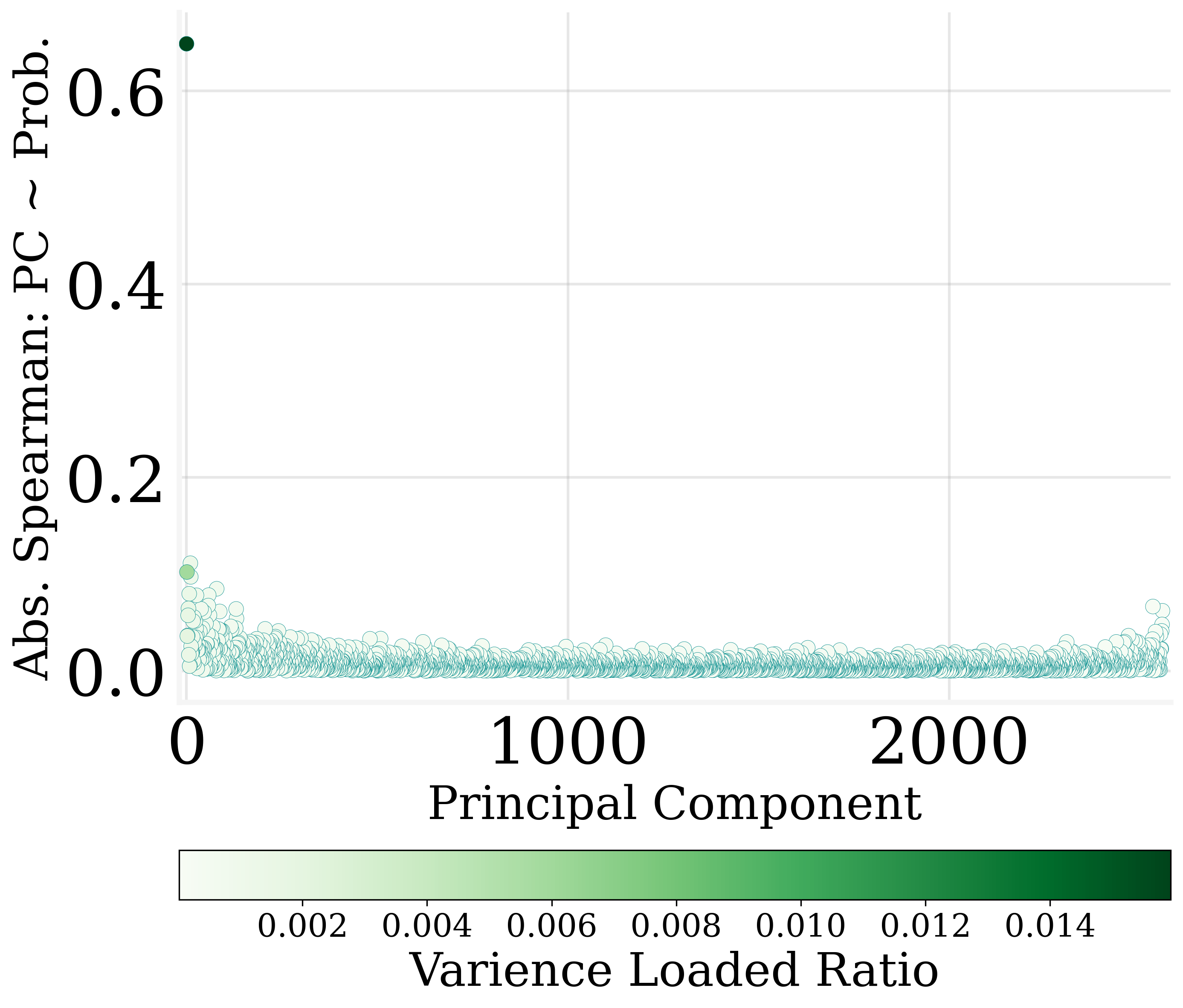
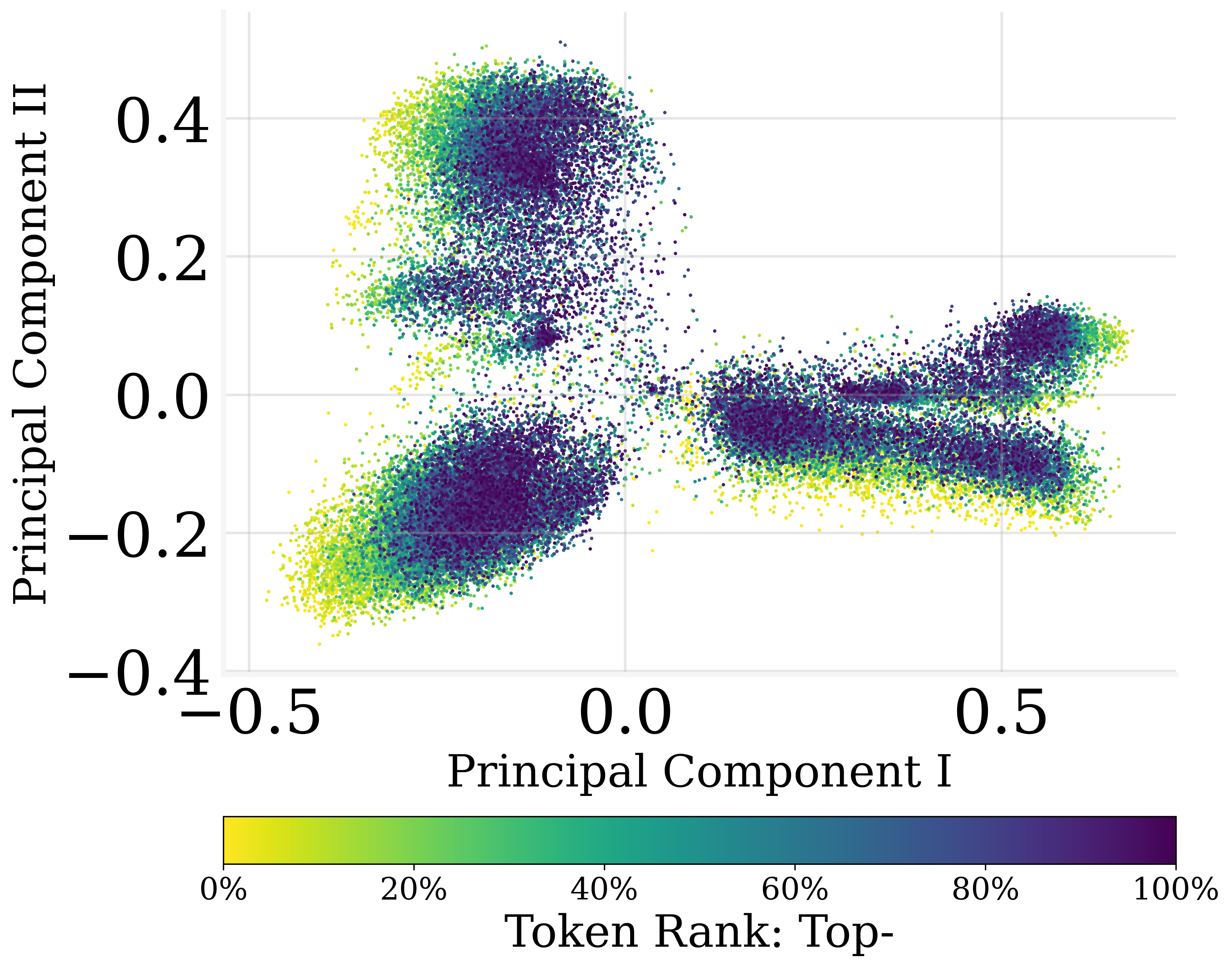
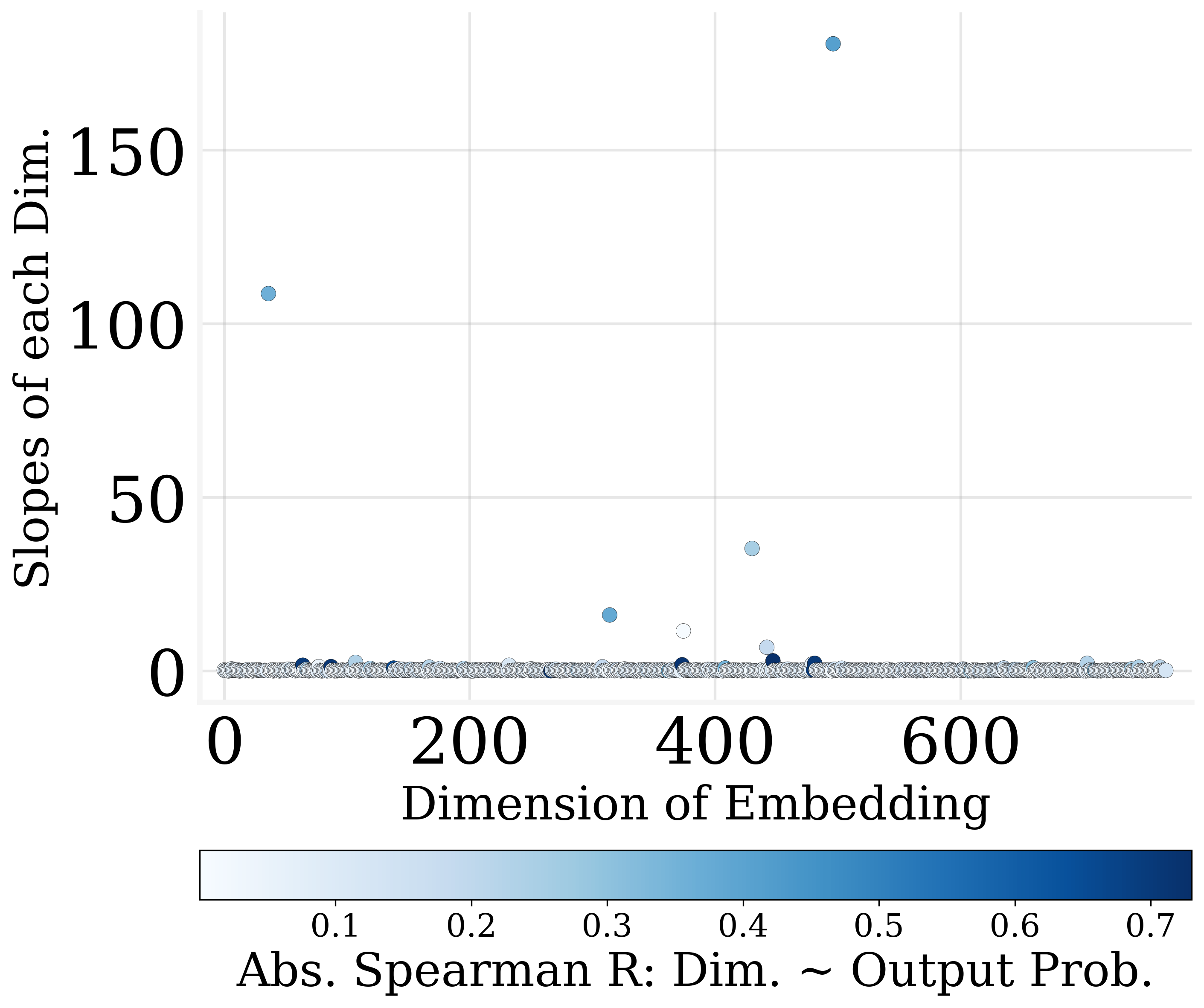
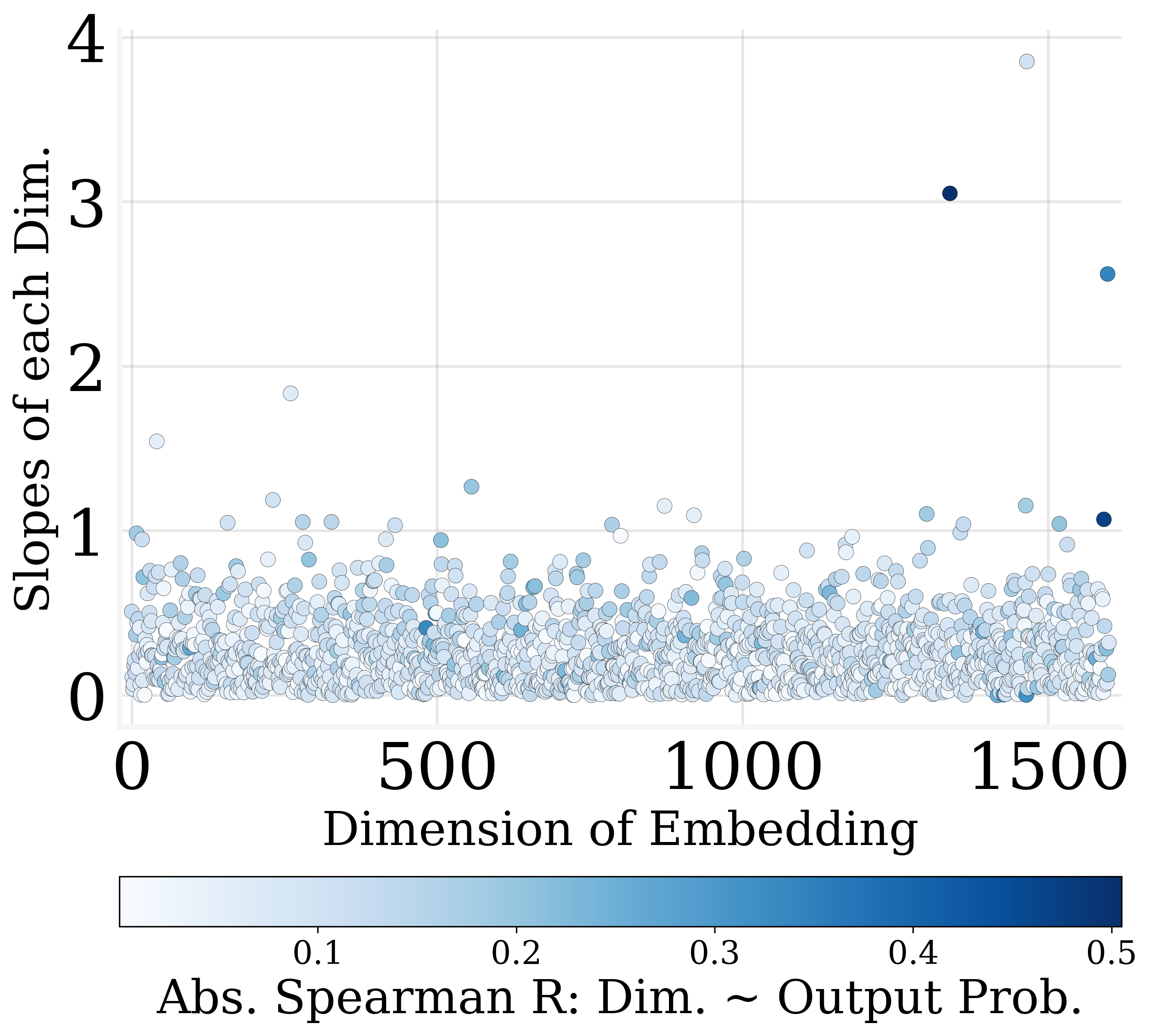
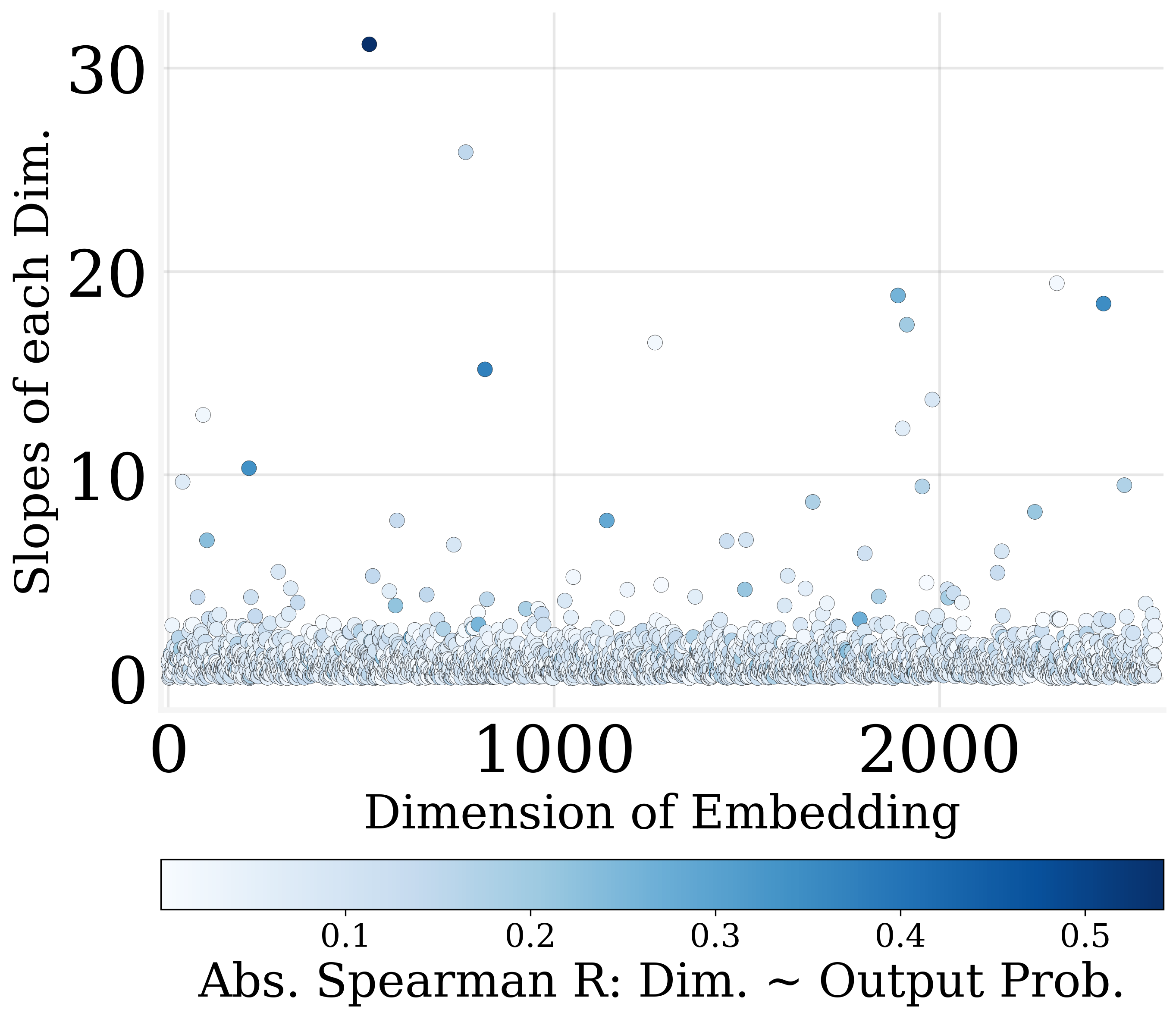
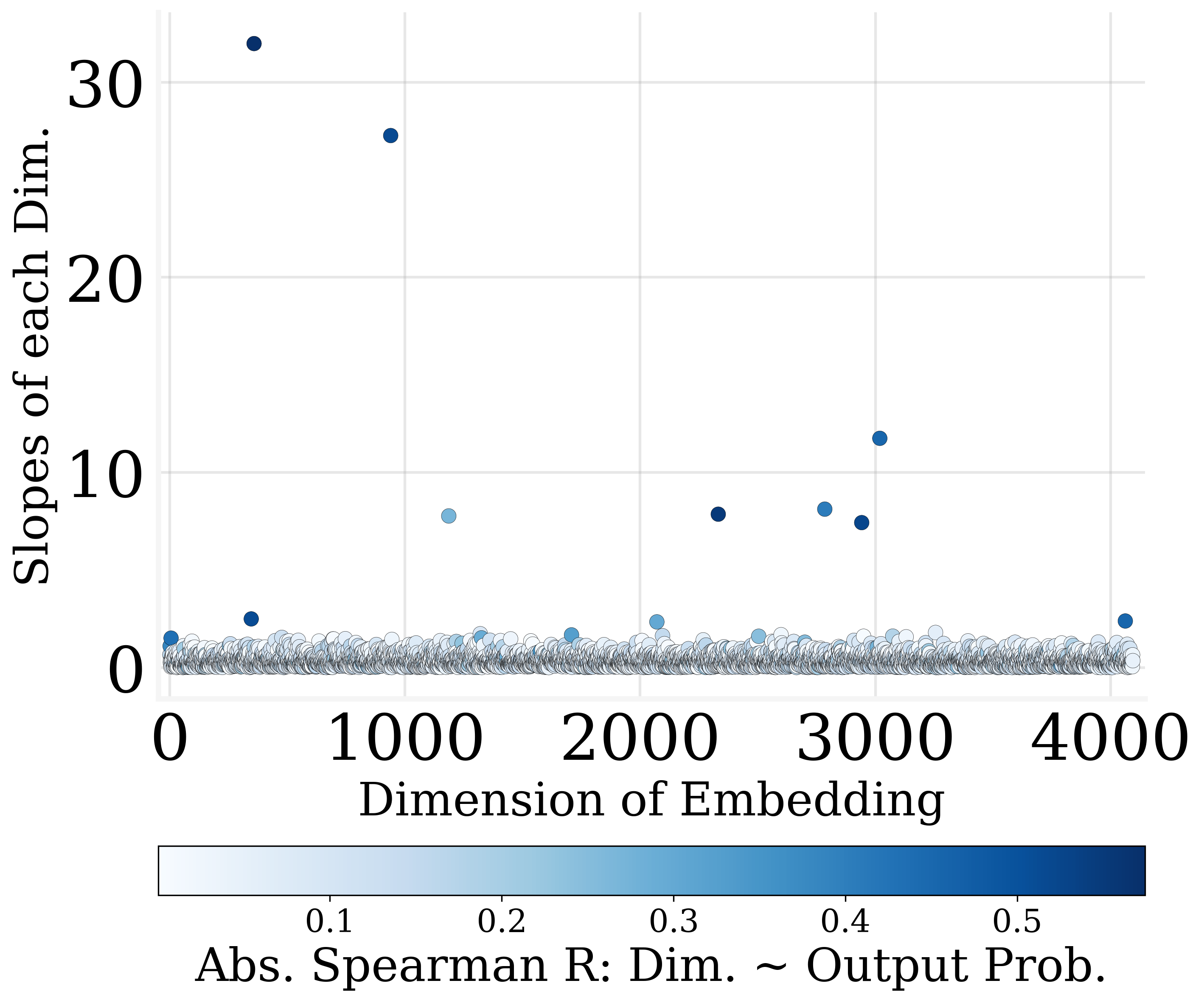
Figure 3: Only a few dimensions of output embedding are strongly correlated to the output probabilities.

Training Dynamics and Frequency Encoding

The paper also explores how LLMs encode the frequency of tokens from the training corpus. It highlights that LMs capture frequency information earlier in the training process than previously understood.

Early Encoding of Frequency Information

Using the Pythia suite, the paper shows that the log-linear relation appears early in the training stage, indicating an intrinsic model capacity to align learned embeddings with corpus token frequencies even before global parameter convergence is observed.

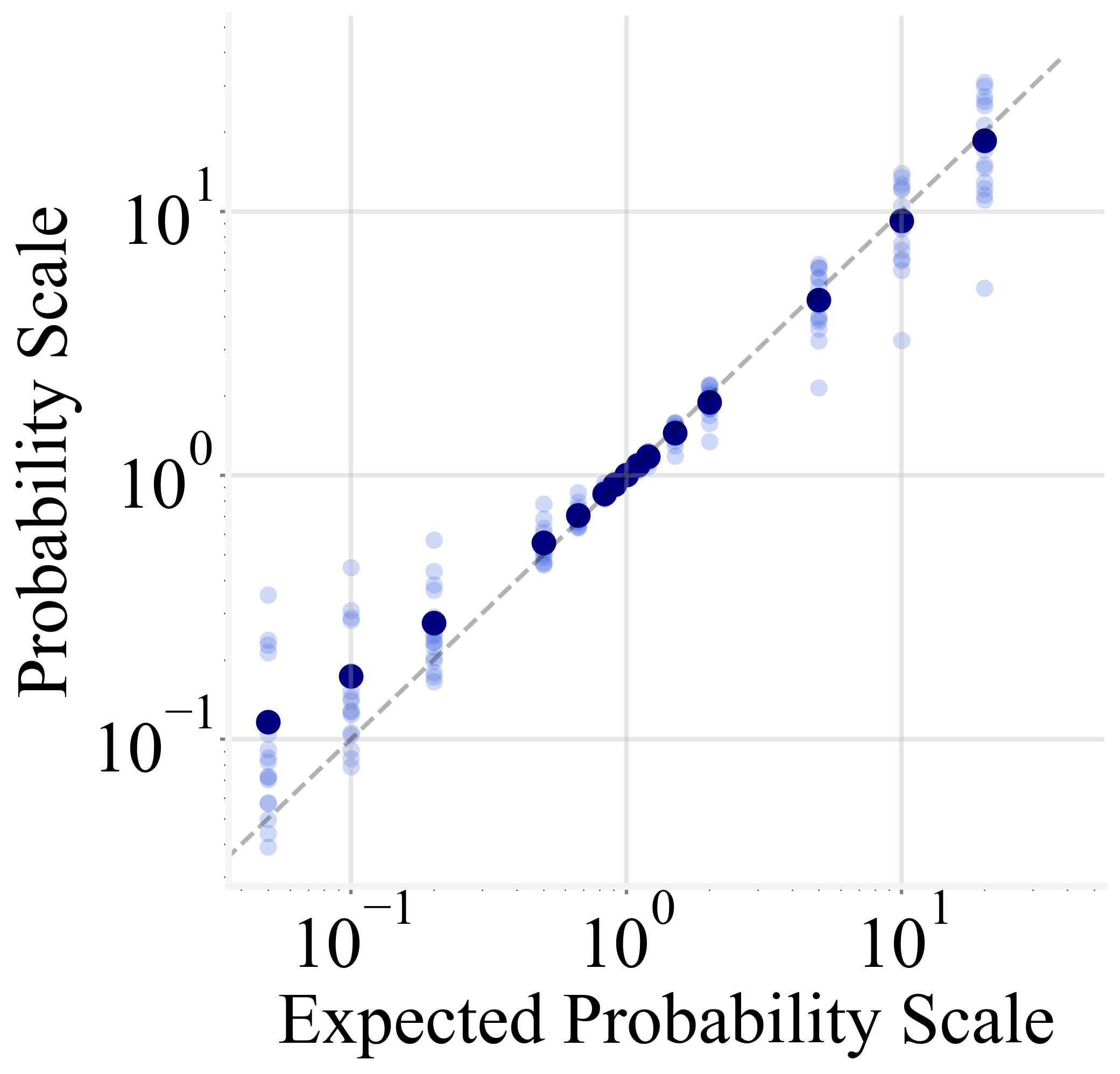
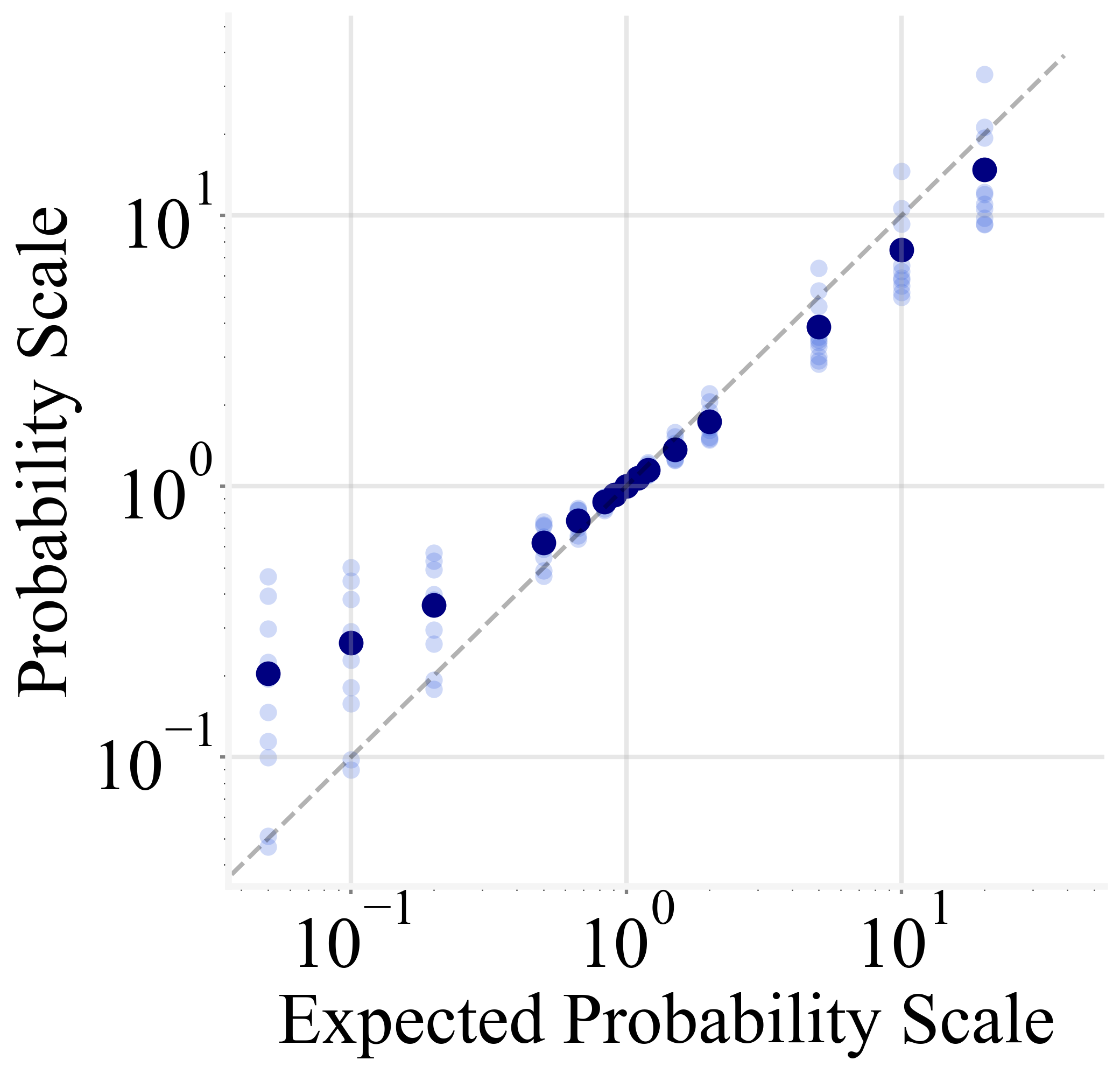
Figure 4: The training dynamics of Pythia illustrating MLR goodness.

Conclusion

The research provides valuable insights into the function and optimization of output embeddings in LLMs, demonstrating both theoretical and practical implications. The findings enable more efficient model editing and pruning techniques, potentially leading to reduced model sizes without compromising performance. This enhances our understanding of LMs' internal workings and could guide future advancements in AI model efficiency and interpretability.