Resonant Sparse Geometry Networks
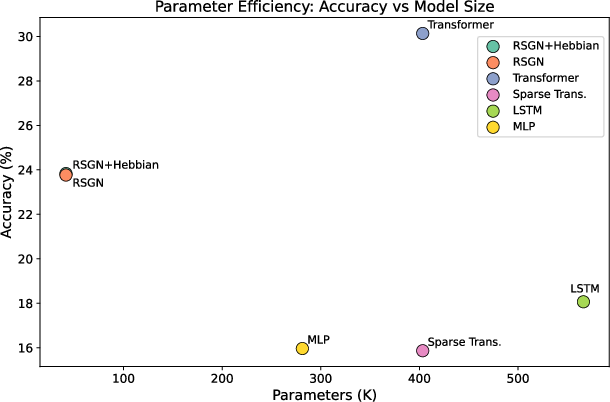
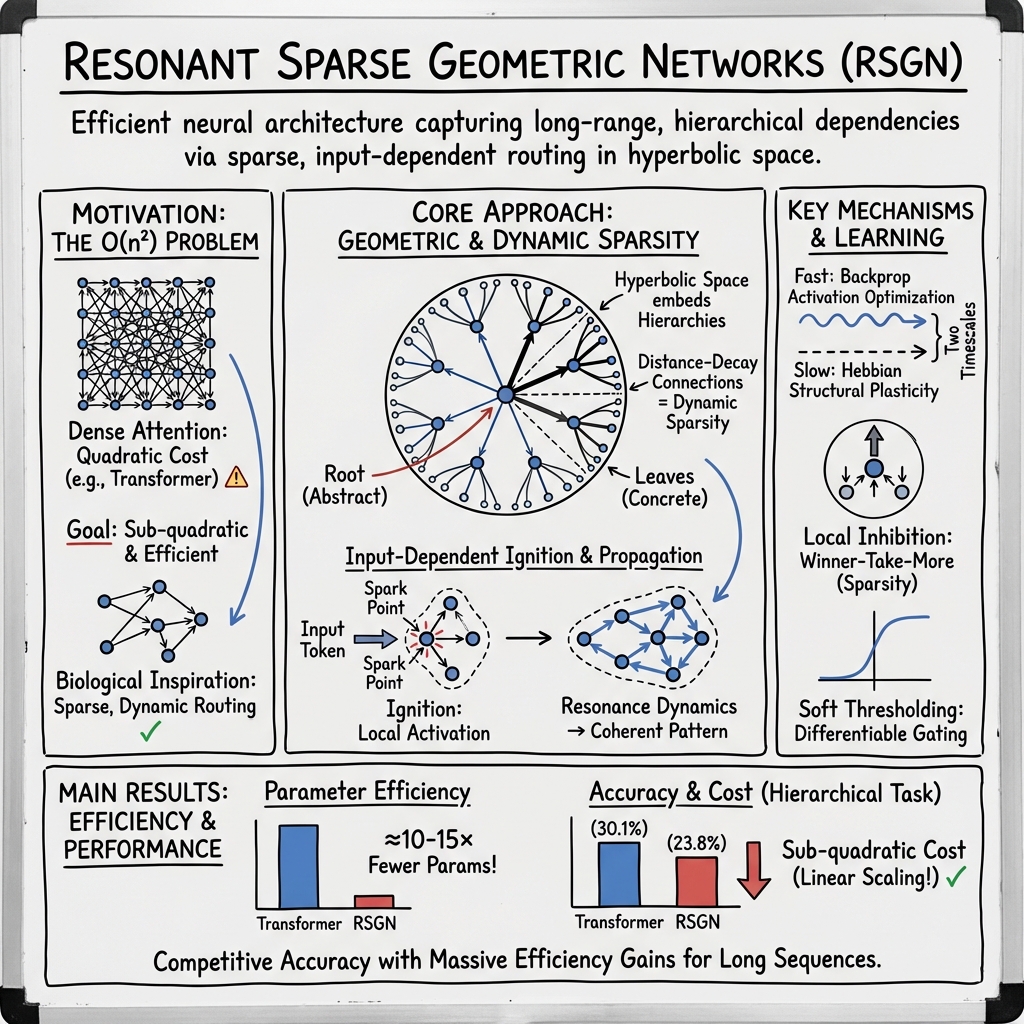
Abstract: We introduce Resonant Sparse Geometry Networks (RSGN), a brain-inspired architecture with self-organizing sparse hierarchical input-dependent connectivity. Unlike Transformer architectures that employ dense attention mechanisms with O(n2) computational complexity, RSGN embeds computational nodes in learned hyperbolic space where connection strength decays with geodesic distance, achieving dynamic sparsity that adapts to each input. The architecture operates on two distinct timescales: fast differentiable activation propagation optimized through gradient descent, and slow Hebbian-inspired structural learning for connectivity adaptation through local correlation rules. We provide rigorous mathematical analysis demonstrating that RSGN achieves O(n*k) computational complexity, where k << n represents the average active neighborhood size. Experimental evaluation on hierarchical classification and long-range dependency tasks demonstrates that RSGN achieves 96.5% accuracy on long-range dependency tasks while using approximately 15x fewer parameters than standard Transformers. On challenging hierarchical classification with 20 classes, RSGN achieves 23.8% accuracy (compared to 5% random baseline) with only 41,672 parameters, nearly 10x fewer than the Transformer baselines which require 403,348 parameters to achieve 30.1% accuracy. Our ablation studies confirm the contribution of each architectural component, with Hebbian learning providing consistent improvements. These results suggest that brain-inspired principles of sparse, geometrically-organized computation offer a promising direction toward more efficient and biologically plausible neural architectures.
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Explanation of “Resonant Sparse Geometry Networks” (RSGN)
1) What this paper is about (overview)
This paper introduces a new kind of AI model called a Resonant Sparse Geometry Network (RSGN). It tries to learn and think more like a brain: using only a small part of the network at a time, routing information based on the input, and slowly changing its connections over time. The goal is to make AI models that are both powerful and much more efficient than today’s Transformers, especially for long sequences like long documents.
2) The main questions the paper asks
- Can we build a model that only activates a small, relevant part of itself for each input, instead of using everything all the time?
- Can we organize the model’s “neurons” in a smart geometry so that nearby neurons naturally work together and faraway ones don’t, leading to fewer, smarter connections?
- Can we separate fast learning (tuning activations for the current input) from slow learning (gradually adjusting which neurons are connected), similar to how brains learn?
- Will this approach be accurate while using far fewer parameters and less computation than Transformers, especially on tasks that need long-range connections?
3) How the model works (methods explained simply)
Think of the model as a city of “nodes” (like tiny processors). Two big ideas make it different:
- A special map for the city: The nodes live in a special curved space called hyperbolic space. You can imagine it like a disk where there’s surprisingly more “room” near the edges than near the center. This kind of space is great at fitting tree-like hierarchies: general concepts stay near the center, and very specific ones sit near the edges. Distance on this map controls how strongly nodes can talk to each other—closer means stronger, like how Wi‑Fi is stronger when you’re near the router.
- Input-dependent ignition: When a new input comes in (like a sentence), it creates “spark points” on the map. Only nodes near those spark points light up and start working. This means the model doesn’t waste energy running everything at once—just the parts that matter for this input.
Once nodes light up, they pass messages to nearby active nodes. There’s a “soft threshold” that decides whether a node stays active, and “local inhibition,” which is a gentle competition so that only a few strong signals win out (like a classroom discussion where only the loudest or most relevant ideas keep going).
Learning happens on two speeds:
- Fast learning: During each training step, the model uses regular gradient descent (the same trick most neural networks use) to improve the way activations flow and how outputs are computed.
- Slow learning: Over many steps, the connections between frequently co-active nodes get stronger (Hebbian learning: “neurons that fire together, wire together”), and rarely used connections fade away. This slowly reorganizes the city map so useful pathways get more convenient.
A key benefit: Instead of every token talking to every other token (which is what Transformers do and costs a lot), each node in RSGN mostly talks to a small neighborhood. In simple terms, if Transformers are like everyone in a classroom whispering to everyone else at once, RSGN is like whispering only to a few nearby classmates—much cheaper and still effective if the seating plan is smart.
4) What they found (results) and why it matters
The authors tested RSGN on two kinds of hard problems:
- Hierarchical classification (20 classes): The patterns were layered—some were local, some medium-range, some global—like a puzzle hidden at multiple scales. RSGN got 23.8% accuracy using only 41,672 parameters. A standard Transformer scored higher (30.1%) but needed about 10× more parameters (403,348). Compared to guessing (5%), RSGN is almost 5× better while staying tiny. That’s strong efficiency.
- Long-range dependency (needs info from both start and end of a long sequence): RSGN reached 96.5% accuracy with around 15× fewer parameters than a Transformer or LSTM, which both hit 100%. So RSGN is very close in accuracy while being much smaller and more efficient—important for long documents and contexts.
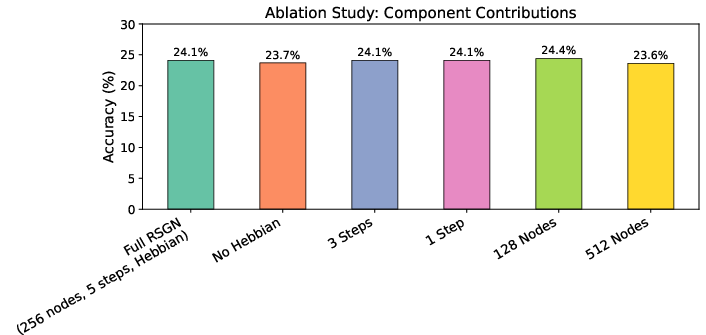
They also ran ablation studies (turning parts of the model on/off) and found:
- The slow, brain-like Hebbian learning consistently helped.
- Performance stayed fairly stable across reasonable settings, showing the model is robust.
- Using more nodes didn’t always help on small datasets, hinting at a sweet spot for model size.
Why this matters:
- Efficiency: RSGN can handle long-range problems using much less compute and memory than Transformers.
- Flexibility: It adapts its active connections to each input, rather than using the same pattern every time.
- Biological inspiration: It moves AI a bit closer to how real brains might work—sparse activity, local competition, and slow structural change.
5) What this could mean next (impact and implications)
If ideas like RSGN keep working, future AI could:
- Process very long texts, videos, or logs without exploding in cost.
- Run faster and cheaper on everyday hardware, making AI more accessible and greener (less energy-hungry).
- Learn in a more brain-like way by growing and pruning connections over time, potentially leading to models that are more adaptable, explainable, and stable.
In short, RSGN suggests a promising path: smarter routing, sparse activity, and geometry-aware design can deliver strong results with far fewer parameters. It doesn’t fully beat Transformers yet, but it shows how we might build the next generation of efficient, brain-inspired AI systems.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
The paper leaves the following points unresolved; addressing them would make the claims more robust and guide future work:
- Real-world validation: No experiments on standard benchmarks (e.g., Long Range Arena, PathX, WikiText, ImageNet, graph tasks) or real datasets; need head-to-head comparisons against state-of-the-art efficient Transformers (Performer, BigBird, Linformer), state-space models (S4, Mamba), and MoE on long-context and hierarchical tasks.
- End-to-end complexity vs sequence length: The abstract claims complexity, but theory uses nodes; clarify the relationship between sequence length , node count , and ignition cost (which appears ). Provide worst-case and typical scaling of k (active set) and m (neighborhood) with and .
- Neighbor search implementation: The paper assumes local neighborhoods in hyperbolic space but does not specify efficient GPU/TPU implementations (e.g., top-k pruning, dynamic sparse kernels, ANN indices in hyperbolic space). Provide concrete algorithms and complexity for constructing and updating neighborhoods per step.
- Convergence of activation dynamics: No guarantees or empirical analysis on whether the iterative propagation plus inhibition converges, oscillates, or diverges. Derive conditions on parameters (e.g., W_h, thresholds, inhibition radius r, temperature T) ensuring convergence to fixed points.
- Learning rules for node positions and levels: The hierarchical level indicator and positions are “slow-learned” but lack explicit update equations. Specify Riemannian optimization for in the Poincaré ball (including curvature, retraction, and regularization near the boundary) and an update rule for .
- Differentiable relaxation inconsistency: Active sets are defined via hard thresholds () during message passing, which is not differentiable. Clarify whether continuous gating (e.g., multiplying messages by ) is used, and provide experiments on temperature annealing schedules and their effect on gradient flow, sparsity, and performance.
- Ignition and sequence order: Initial activation uses a max over tokens, which discards counts and temporal order. Introduce positional/temporal encoding within ignition or propagation, and evaluate on tasks where order is critical (e.g., algorithmic sequences, language modeling).
- Output readout generality: The current readout is tailored to classification. Define and test extensions for sequence-to-sequence tasks, causal decoding, and autoregressive generation (e.g., encoder–decoder RSGN, streaming variants).
- Hebbian plasticity specifics: Provide details on correlation window length, pruning/sprouting thresholds, and topology evolution metrics. Study interactions with backprop (e.g., interference, stability), risks of hub formation or topology collapse, and behavior under continual learning.
- Hyperparameter sensitivity: No systematic analysis of sensitivity to key parameters (τ, σ_ign, inhibition radius r, target sparsity α_target, affinity rank r). Conduct sweeps and report guidelines for stable training across tasks.
- Sparsity measurement: Claims draw on biological sparsity (1–2%), but target α_target is 0.1 and actual activation rates are not reported. Measure and report the fraction of active nodes per step/input, and its effect on accuracy and compute.
- Robustness and generalization: No tests under noise, distribution shift, or adversarial perturbations. Evaluate robustness benefits attributed to sparsity and inhibition, and compare against baselines.
- Hardware efficiency: Parameter counts are reported, but wall-clock time, FLOPs, memory footprint, and throughput/latency are missing. Provide benchmarks showing practical efficiency and discuss implementation challenges with dynamic sparsity on modern accelerators.
- Interpretability of learned geometry: The paper motivates hyperbolic geometry for hierarchies but does not visualize or quantify the learned positions and levels. Analyze whether learned geometries align with task hierarchies (e.g., via tree distortion metrics).
- Baseline fairness: Baselines (e.g., “Sparse Transformer”) are simple and may be under-tuned relative to RSGN. Ensure parity in depth, width, training budget, and tuning, and include stronger efficient Transformer variants and SSMs.
- Scalability limits: Experiments use small (≤512) and short sequences (≤128). Test scaling to thousands of nodes and long contexts (≥10k tokens), and report accuracy, stability, and compute trends.
- Expressiveness claims: The universal approximation theorem is a proof sketch relying on existing results; formalize details for dynamic, input-dependent graphs and provide capacity bounds as functions of , , , and sparsity.
- Gradient stability across steps: Analyze vanishing/exploding gradients through iterative propagation with SoftThresh and LayerNorm. Report training curves, diagnose failure modes, and propose stabilizers (e.g., residual gating, skip connections).
- Biological plausibility metrics: Claims of biological inspiration would benefit from quantitative alignment (e.g., activation sparsity distributions, two-timescale adaptation dynamics, inhibitory competition statistics). Measure and compare to neuroscience data.
- Reproducibility: The repository is referenced but not provided. Release code, datasets, configurations, and seeds; report variance across ≥5 seeds and statistical significance of improvements.
Practical Applications
Immediate Applications
The following applications can be prototyped and piloted today, leveraging RSGN’s dynamic sparsity, hyperbolic geometry for hierarchy, and two-timescale learning. They are best suited to tasks with hierarchical structure and/or long-range dependencies where compute/memory budgets are constrained.
- Efficient prefiltering for long-context models (hybrid with Transformers or SSMs)
- Sectors: software, NLP, enterprise search, legal/finance document understanding
- What: Use RSGN to route tokens to small, input-specific neighborhoods and prune token pairs before attention (reducing O(n2) to O(n·k)), or select salient spans for downstream models.
- Tools/products/workflows: “RSGN-Attn” drop-in module; token-pruning preprocessor; PyTorch layer with approximate neighbor retrieval under hyperbolic distance; integration into retrieval-augmented generation pipelines.
- Assumptions/dependencies: Availability of a fast neighborhood index (e.g., FAISS/ScaNN with custom hyperbolic metric or embedding-to-Euclidean proxy); careful joint training to preserve accuracy; monitoring of active-set size k to ensure realized savings.
- Hierarchical taxonomy classification with low parameter count
- Sectors: e-commerce (product taxonomy), content moderation, biomedical coding (ICD/SNOMED), document management
- What: Replace or augment classifiers with RSGN to exploit the task’s tree-like structure (distance-decayed connectivity in hyperbolic space).
- Tools/products/workflows: Taxonomy-aware classifiers; fine-tuning pipelines that initialize node positions from taxonomy graphs; exportable lightweight models for edge inference.
- Assumptions/dependencies: Labeled data that aligns with known hierarchies; stable training under hyperbolic ops; evaluation against hierarchical metrics (e.g., path distance losses).
- On-device pre-summarization and privacy-preserving filtering
- Sectors: mobile, productivity, customer support, healthcare intake (non-diagnostic triage)
- What: Run RSGN locally to compress long texts/transcripts into salient segments before cloud processing, reducing bandwidth and exposure of raw data.
- Tools/products/workflows: Mobile inference libraries (Core ML, TensorRT, ONNX) with RSGN kernels; two-stage mobile→cloud workflows.
- Assumptions/dependencies: Efficient kernels for dynamic sparsity; quantization-aware training; UI/UX signaling confidence and fallbacks when summarization is uncertain.
- Log and telemetry anomaly pre-detection
- Sectors: DevOps/observability, security (SIEM), IoT/edge monitoring
- What: Use ignition + local inhibition to route attention to rare hierarchical patterns across long logs; flag suspicious regions for heavy analyzers.
- Tools/products/workflows: RSGN preprocessing node in data pipelines; streaming inference with sliding windows; integration with alerting systems.
- Assumptions/dependencies: Streaming-friendly implementation; robustness to drift; labeled or self-supervised objectives aligned with operational KPIs.
- Memory/energy-efficient model deployments in constrained environments
- Sectors: IoT, automotive ECUs, wearables, robotics (perception side-tasks)
- What: Replace some dense attention blocks or full sequence models with RSGN to cut parameters and FLOPs for non-critical, auxiliary tasks.
- Tools/products/workflows: Model compression playbooks; mixed-precision and sparsity-aware kernels; watchdogs for active-node caps.
- Assumptions/dependencies: Safety certification for automotive/robotics requires extensive validation; maintain timing determinism under dynamic routing.
- Research testbed for biologically inspired learning and sparsity
- Sectors: academia (ML, neuroscience), industrial research labs
- What: Study two-timescale learning (backprop + Hebbian), input-dependent routing, and hyperbolic embeddings; benchmark against efficient attention/SSM variants.
- Tools/products/workflows: Public codebase; ablation suites; metrics dashboards for k (active set), m (neighborhood size), sparsity, and energy.
- Assumptions/dependencies: Reproducibility across seeds/datasets; standardized evaluation beyond synthetic tasks (e.g., Long Range Arena, taxonomic datasets).
- Curriculum modules and teaching labs
- Sectors: education
- What: Hands-on labs for hyperbolic geometry in ML, sparse dynamic routing, and Hebbian updates; compare to Transformers and SSMs.
- Tools/products/workflows: Jupyter notebooks; visualization of Poincaré disk positions and activation “ignitions.”
- Assumptions/dependencies: Didactic datasets; stable visualization tools for hyperbolic geometry.
- Knowledge-graph and taxonomy-aware retrieval reranking
- Sectors: search/recommendation, knowledge management
- What: Use RSGN to navigate hierarchical category space for coarse reranking before fine re-ranking by heavier models.
- Tools/products/workflows: RSGN-based hierarchical gate preceding rankers; batch-friendly neighbor lookup.
- Assumptions/dependencies: Graph-to-position initialization; ensuring recall is preserved after gating.
Long-Term Applications
These opportunities likely require additional research, scaling studies, systems integration, or hardware support to realize at production scale.
- Long-context foundation models with near-linear scaling
- Sectors: NLP, code, multimodal assistants
- What: Train RSGN-based or hybrid architectures that sustain million-token contexts by routing computation through sparse, input-specific neighborhoods.
- Tools/products/workflows: Distributed training for dynamic sparse graphs; curriculum schedules for temperature/threshold annealing; memory-augmented hybrids (RSGN + SSMs).
- Assumptions/dependencies: Demonstrated robustness on real corpora; compiler/runtime support for dynamic sparsity on GPUs/accelerators; improved optimization techniques for stability.
- Neuromorphic and event-driven deployments
- Sectors: energy-efficient AI, edge computing, defense
- What: Map RSGN’s sparse, local, input-dependent computation and slow structural plasticity onto spiking/neuromorphic hardware.
- Tools/products/workflows: Event-driven kernels; local-learned plasticity modules; geometry-aware routing primitives.
- Assumptions/dependencies: Hardware support for neighborhood competition and learnable geometry; translation of hyperbolic distance or equivalent locality into on-chip routing.
- Healthcare sequence modeling with privacy and long-range dependencies
- Sectors: healthcare (EHR modeling, triage, longitudinal patient trajectories), bioinformatics (hierarchical ontologies)
- What: Use RSGN to integrate sparse cues across years of EHRs or hierarchical codes; on-prem or on-device triage with reduced compute.
- Tools/products/workflows: Federated or on-prem training; auditability tools for activation patterns; ontology-initialized node positions.
- Assumptions/dependencies: Regulatory compliance (HIPAA/GDPR); clinical validation; bias and drift monitoring; interpretable readouts from active nodes.
- Real-time hierarchical perception and control in robotics
- Sectors: robotics, autonomous systems
- What: Dynamic routing from sensory “ignitions” to specialized modules; local inhibition for conflict resolution; hierarchical control embedded in geometry.
- Tools/products/workflows: ROS integration; real-time scheduling for bounded k and latency; simulation-to-real adaptation.
- Assumptions/dependencies: Hard real-time constraints; safety verification; robustness to partial observability and adversarial conditions.
- Grid, industrial, and financial time-series monitoring at scale
- Sectors: energy, manufacturing, finance
- What: Detect rare, hierarchical failure modes in long multivariate streams; route computation to anomalous regions while keeping overall cost low.
- Tools/products/workflows: Streaming RSGN operators; hierarchical fault taxonomies; alert triage dashboards that surface active-node patterns.
- Assumptions/dependencies: High-throughput streaming implementations; semi-supervised learning for rare events; reliability guarantees.
- Adaptive tutoring and knowledge modeling
- Sectors: education technology
- What: Represent student knowledge hierarchies in hyperbolic space; input-dependent routing to appropriate content; slow structural updates reflecting mastery.
- Tools/products/workflows: Skill graph initialization; per-learner structural plasticity; explainable student models via active node traces.
- Assumptions/dependencies: Validated pedagogical mappings; data sparsity; fairness and accessibility requirements.
- Policy and sustainability frameworks for “Green AI” routing
- Sectors: policy and governance
- What: Promote input-dependent sparse computation standards and benchmarks; incentivize architectures that document realized FLOPs/energy savings.
- Tools/products/workflows: Reporting templates for active-set sizes and compute; procurement guidelines favoring dynamic sparsity; carbon-aware scheduling.
- Assumptions/dependencies: Community-accepted metrics; third-party audits; alignment with existing AI governance frameworks.
- Compiler/runtime ecosystems for dynamic sparse geometry computation
- Sectors: AI infrastructure
- What: Create kernels and graph compilers that natively support input-dependent neighborhoods, hyperbolic distance ops, and two-timescale updates.
- Tools/products/workflows: XLA/TVM/MLIR extensions; specialized ANN libraries for non-Euclidean metrics; profilers that track k, m, and wall-clock savings.
- Assumptions/dependencies: Vendor buy-in; stability of the RSGN operator set; cross-hardware portability.
- Consumer assistants with offline long-memory
- Sectors: mobile, wearables, smart home
- What: Lightweight assistants that maintain long personal histories (notes, transcripts) with on-device routing and periodic slow consolidation.
- Tools/products/workflows: Privacy-preserving memory stores; user controls over structural updates; fallbacks to cloud models when confidence is low.
- Assumptions/dependencies: Productization of training/inference on device; battery life constraints; transparent UX for adaptive behavior.
Cross-cutting assumptions and risks to feasibility
- Generalization from synthetic to real-world data is unproven at large scale; benchmarks across language, vision, and multimodal tasks are needed.
- Two-timescale learning introduces operational complexity (e.g., scheduling Hebbian updates, stability under global reward signals).
- Dynamic sparsity complicates compilation and latency predictability; systems support (compilers, kernels, ANN) is a key dependency.
- Hyperbolic operations require numerically stable implementations and practical neighbor search; approximations may trade accuracy for speed.
- Regulatory and safety contexts (healthcare, automotive, finance) demand rigorous validation, interpretability, and monitoring of sparsity/routing behavior.
Glossary
- Ablation study: A controlled analysis where components of a model are removed or altered to assess their contribution. "Our ablation studies confirm the contribution of each architectural component, with Hebbian learning providing consistent improvements."
- AdamW optimizer: An optimization algorithm that decouples weight decay from gradient-based updates for better generalization. "We use AdamW optimizer~\cite{loshchilov2017decoupled} with learning rate , weight decay , and cosine annealing schedule."
- Backpropagation: The standard algorithm for computing gradients in neural networks by propagating errors backward through layers. "We propose a hybrid learning rule combining backpropagation for fast weight updates with Hebbian structural plasticity for slow topological adaptation, offering a biologically plausible alternative to end-to-end gradient-based structure learning (\autoref{sec:learning})."
- Basal ganglia: A group of subcortical brain structures involved in learning and action selection, often tied to reward-modulated plasticity. "A global reward signal modulates plasticity strength, analogous to dopaminergic modulation of synaptic plasticity in the basal ganglia and cortex~\cite{schultz1997neural,reynolds2001cellular}."
- BigBird: An efficient Transformer variant that combines local, random, and global attention to achieve linear complexity. "BigBird~\cite{zaheer2020big} extends this approach with random attention connections and global tokens, achieving linear complexity while preserving theoretical expressiveness."
- Bidirectional LSTM: A recurrent neural network that processes sequences in both forward and backward directions to capture context. "LSTM: Bidirectional LSTM with 2 layers"
- Conformal factor: A scaling function in a Riemannian metric that preserves angles while altering distances. "The conformal factor $\lambda_{#1{x} = 2/(1 - \|#1{x}\|^2)$ causes distances to expand as points approach the boundary, encoding the exponential growth of volume characteristic of hyperbolic geometry."
- Cosine annealing schedule: A learning rate schedule that follows a cosine decay pattern to improve convergence. "We use AdamW optimizer~\cite{loshchilov2017decoupled} with learning rate , weight decay , and cosine annealing schedule."
- Divisive normalization: A neural computation where a neuron's activity is normalized by the activity of its neighbors, promoting competition. "This implements divisive normalization, a canonical neural computation observed across sensory systems~\cite{carandini2012normalization}."
- Dopaminergic modulation: The influence of dopamine on synaptic plasticity and learning signals in the brain. "A global reward signal modulates plasticity strength, analogous to dopaminergic modulation of synaptic plasticity in the basal ganglia and cortex~\cite{schultz1997neural,reynolds2001cellular}."
- Equilibrium Propagation: A learning framework that computes gradients via network dynamics settling to equilibrium, aiming for biological plausibility. "Equilibrium Propagation~\cite{scellier2017equilibrium} provides a biologically plausible alternative to backpropagation by computing gradients through network dynamics at equilibrium."
- FAVOR+: A random feature method used to approximate softmax attention for linear-time computation. "Performer~\cite{choromanski2020rethinking} uses random feature approximations of the softmax kernel (FAVOR+) to decompose attention computation, enabling linear-time attention through the associativity of matrix multiplication."
- Geodesic distance: The shortest-path distance between points under a given geometry or metric. "The geodesic distance between points $#1{p}_i, #1{p}_j \in B^d$ is given by the closed-form expression:"
- Global workspace theory: A cognitive theory proposing that conscious processing arises from widespread broadcasting of information across specialized modules. "The resonance metaphor reflects that stable activation patterns emerge through iterative settling, analogous to the global workspace theory of consciousness where coherent representations arise from competitive dynamics among specialized processors~\cite{baars1988cognitive,dehaene2011experimental}."
- Hebbian learning: A correlation-based learning principle summarized as “neurons that fire together wire together.” "Slow learning uses local Hebbian rules where co-activated nodes strengthen their connections and drift toward each other in the embedding space, while unused connections decay and eventually prune."
- HiPPO framework: A mathematical framework for continuous-time state space models that preserves history efficiently. "Structured State Space Sequence models (S4)~\cite{gu2021efficiently} achieve linear complexity through continuous-time state space formulations with carefully parameterized transition matrices based on the HiPPO framework~\cite{gu2020hippo}."
- Hyperbolic geometry: A non-Euclidean geometry with constant negative curvature, well-suited for representing hierarchies. "Hyperbolic geometry has attracted increasing attention in machine learning due to its natural capacity for representing hierarchical structures."
- Ignition: An input-dependent activation process that initiates activity in specific network regions based on the input. "We implement input-dependent ignition where input tokens create ``spark points'' in the embedding space, activating only nearby nodes and establishing sparse initial activation patterns."
- Layer normalization (LayerNorm): A technique that normalizes activations across features within a layer to stabilize training. "State vectors combine new information with residual connections (\autoref{eq:state_update}), stabilized by LayerNorm~\cite{ba2016layer}."
- Linformer: An efficient Transformer variant that projects keys/values to lower-dimensional spaces to make attention linear in sequence length. "Linformer~\cite{wang2020linformer} projects keys and values to lower-dimensional spaces, achieving complexity under the assumption that attention matrices are approximately low-rank."
- Local inhibition: A mechanism where nearby units suppress each other’s activity to encourage sparse, competitive representations. "To prevent activation explosion and encourage winner-take-more competition, we apply local inhibition within spatial neighborhoods."
- Lottery Ticket Hypothesis: The idea that large networks contain sparse subnetworks that can train to comparable performance when isolated. "The Lottery Ticket Hypothesis~\cite{frankle2018lottery} demonstrates that sparse subnetworks exist within dense networks that can match full network performance when trained in isolation."
- Mamba architecture: A selective state space model introducing content-dependent transitions for sequence modeling. "The recent Mamba architecture~\cite{gu2023mamba} extends this framework with selective state spaces, introducing content-dependent processing through input-dependent transition parameters."
- Mixture of Experts (MoE): A model that routes inputs to specialized subnetworks (experts) via learned gating for scalable capacity. "Mixture of Experts (MoE)~\cite{shazeer2017outrageously,fedus2022switch} routes inputs to different expert subnetworks through learned gating functions, achieving input-dependent computation allocation that scales model capacity without proportional computational cost."
- Predictive Coding: A theory where the brain minimizes prediction errors through hierarchical inference and feedback. "Predictive Coding~\cite{rao1999predictive,friston2005theory} frames neural computation as hierarchical prediction and error correction, offering a functional account of cortical processing that connects perception, action, and learning."
- Riemannian metric: A smoothly varying inner product on tangent spaces defining distances and angles on a manifold. "The Poincar " e ball $B^d = \{#1{x} \in R^d : \|#1{x}\| < 1\}$ is the open unit ball equipped with the Riemannian metric"
- Softplus: A smooth approximation to ReLU given by log(1+ex), often used for positive outputs. "where (softplus with bias) favors feedforward information flow"
- Soft threshold: A differentiable gating function that smoothly approximates a hard threshold. "The differentiable soft threshold activation is"
- Spike-timing-dependent plasticity (STDP): A synaptic learning rule where the timing of spikes determines changes in synaptic strength. "This principle has been formalized in various spike-timing-dependent plasticity (STDP) rules~\cite{markram1997regulation,bi1998synaptic}"
- Structured State Space Sequence models (S4): Sequence models using continuous-time state spaces to achieve efficient long-range processing. "Structured State Space Sequence models (S4)~\cite{gu2021efficiently} achieve linear complexity through continuous-time state space formulations with carefully parameterized transition matrices based on the HiPPO framework~\cite{gu2020hippo}."
- Synaptic pruning: The activity-dependent removal of weak or unused connections over time. "and activity-dependent synaptic pruning during development and throughout life~\cite{huttenlocher1979synaptic,petanjek2011extraordinary}."
- Synaptic scaling: A homeostatic plasticity mechanism that adjusts synaptic strengths to maintain stable activity. "This homeostatic mechanism maintains approximately constant sparsity levels despite changing input statistics, analogous to synaptic scaling in biological neurons~\cite{turrigiano2004homeostatic}."
- Universal approximation theorem: A result stating that sufficiently large neural networks can approximate any continuous function on compact sets. "By the universal approximation theorem for feedforward networks with sufficient width~\cite{cybenko1989approximation,hornik1989multilayer}, the result follows."
- Winner-take-more: A competitive dynamic where stronger activations suppress but do not completely eliminate weaker ones. "implementing a winner-take-more competition that mirrors lateral inhibition in biological neural circuits~\cite{isaacson2011smell,carandini2012normalization}."
Collections
Sign up for free to add this paper to one or more collections.