Gradient Descent as Implicit EM in Distance-Based Neural Models (2512.24780v1)

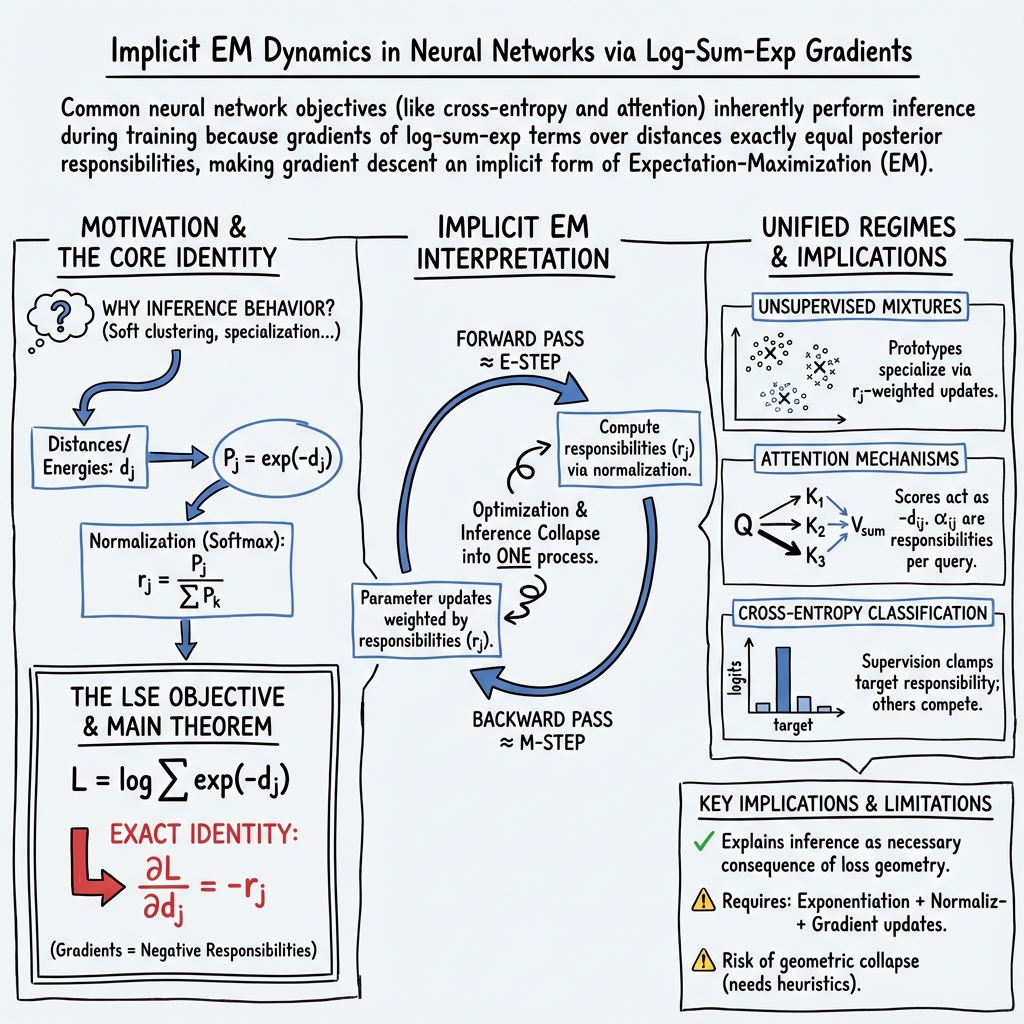
Abstract: Neural networks trained with standard objectives exhibit behaviors characteristic of probabilistic inference: soft clustering, prototype specialization, and Bayesian uncertainty tracking. These phenomena appear across architectures -- in attention mechanisms, classification heads, and energy-based models -- yet existing explanations rely on loose analogies to mixture models or post-hoc architectural interpretation. We provide a direct derivation. For any objective with log-sum-exp structure over distances or energies, the gradient with respect to each distance is exactly the negative posterior responsibility of the corresponding component: $\partial L / \partial d_j = -r_j$. This is an algebraic identity, not an approximation. The immediate consequence is that gradient descent on such objectives performs expectation-maximization implicitly -- responsibilities are not auxiliary variables to be computed but gradients to be applied. No explicit inference algorithm is required because inference is embedded in optimization. This result unifies three regimes of learning under a single mechanism: unsupervised mixture modeling, where responsibilities are fully latent; attention, where responsibilities are conditioned on queries; and cross-entropy classification, where supervision clamps responsibilities to targets. The Bayesian structure recently observed in trained transformers is not an emergent property but a necessary consequence of the objective geometry. Optimization and inference are the same process.

• The paper proves that the gradient of log-sum-exp objectives equals the negative posterior responsibilities, thereby implementing implicit EM in neural models.
• It unifies unsupervised clustering, transformer attention, and cross-entropy classification under a single geometric framework, clarifying diverse learning regimes.
• The work offers practical insights by showing how responsibility-weighted updates naturally arise from gradient descent, guiding future model and objective design.

Gradient Descent as Implicit EM in Distance-Based Neural Models

Summary of Main Contributions

This paper demonstrates that gradient descent on objectives of the form $L = \log \sum_j \exp(-d_j)$, where $d_j$ are distances (or energies) to learned prototypes, implements a form of expectation-maximization (EM) automatically. The central theorem states that the gradient of $L$ with respect to each distance is exactly the negative posterior responsibility of the corresponding component: $\partial L / \partial d_j = -r_j$, with $r_j = \exp(-d_j) / \sum_k \exp(-d_k)$. This is an algebraic identity, not an approximation or analogy, and holds for any differentiable, distance-based log-sum-exp objective. As a result, inference and optimization are unified—responsibilities are not auxiliary quantities to be computed, but emerge as gradients applied via backpropagation.

The result offers a unification of mixture models (unsupervised regime), attention mechanisms (conditional regime), and cross-entropy classification (constrained regime) within a single analytic framework. The different settings correspond to distinct constraints on the responsibility structure, but all derive their EM-like dynamics directly from the objective geometry. This analysis also clarifies the origin of soft clustering, prototype specialization, and Bayesian behaviors observed across diverse neural architectures.

Theoretical Formulation

The analysis builds on a geometric interpretation of neural outputs as distances or energies (in the sense of Mahalanobis or Euclidean metrics), rather than as uncalibrated scores or confidences. Within this framework, the log-sum-exp (LSE) objective acts as the log marginal likelihood over an unnormalized exponential likelihood for each prototype or component:

$L(x) = \log \sum_{j=1}^{K} \exp(-d_j(x))$

where each $d_j$ is the computed "distance" from input $x$ to prototype $j$. This setting encompasses cross-entropy loss (where logits correspond to negative distances), transformer attention mechanisms (where dot products act as negative energies/distances), and unsupervised mixture modeling.

The key theorem is derived by straightforward differentiation:

$$\frac{\partial L}{\partial d_j} = -\frac{\exp(-d_j)}{\sum_k \exp(-d_k)} = -r_j$$

Thus, during training, gradient descent distributes parameter updates across the prototypes in proportion to their responsibilities. These EM-like dynamics arise solely from the loss geometry and the use of gradient-based optimization.

Implications Across Learning Regimes

Unsupervised Mixture Modeling

When training with an unsupervised LSE objective, responsibilities are fully latent and learned prototypes self-organize into clusters. The learning dynamic mirrors classical EM: the forward pass computes posterior responsibilities; the backward pass applies responsibility-weighted updates. The implicit soft assignment and prototype specialization observed in mixture models and clustering tasks are direct mathematical consequences of gradient flow, not emergent or accidental phenomena.

Transformer Attention and Conditional Mixtures

When the assignment is conditional (as in transformers), attention weights are mathematically identical to responsibilities. For a query $q$ and set of keys $\{k_j\}$, attention computes (possibly negative) distances, exponentiates, and normalizes to yield attention weights:

$$\alpha_{ij} = \frac{\exp(s_{ij})}{\sum_m \exp(s_{im})}$$

These weights act as responsibilities. Value parameter updates in the backward pass are automatically weighted by attention. Feedback connections and prototype refinement in attention heads thus reflect implicit EM across function space, as opposed to explicit parameter updates in classical mixture models.

Cross-Entropy Classification and Supervised Constraints

Supervision (via hard labels) imposes constraints on responsibilities, enforcing a target assignment of responsibility $1$ to the correct class. The cross-entropy objective, interpreted via distances, leads to gradients that enhance separation for the correct class and suppress probability mass for rivals, proportional to their current responsibilities. The update for each class decomposes as:

$$\frac{\partial L}{\partial d_j} = r_j - \mathbb{1}[j = y]$$

where $y$ is the target class. This mechanism naturally implements competition and aligns with EM-like prototype learning under supervision.

Practical and Theoretical Consequences

The result reframes usual distinctions between optimization and inference, establishing their equivalence under a broad class of neural objectives. Optimization (gradient descent on geometric losses) becomes indistinguishable from inference (posterior responsibility assignment), when viewed through this lens.

Pragmatically, this insight offers a rigorous foundation for previously heuristic claims that neural attention and classification mechanisms perform Bayesian inference or "resemble" mixture models. It specifies precise conditions under which implicit EM dynamics arise (the necessity of exponentiation, normalization, and gradient-based optimization), points out when these dynamics break down (e.g., multi-label objectives without normalization), and clarifies the root cause of phenomena like prototype collapse (absence of a volume penalty analogous to the covariance term in Gaussian mixtures).

For interpretability, responsibilities are directly observable in gradient signals during training. For architecture and objective design, the analysis distinguishes effects attributable to the loss structure from those due to model architecture, recommending the log-sum-exp form when responsibility-weighted adaptation is desirable, and highlighting its limits (e.g., closed-world assignment, lack of an explicit "none" class, degeneracy in volume control).

Relationship to Prior Work

The paper's results sharpen and formalize empirical observations of Bayesian geometry in transformer attention reported by Aggarwal et al. ["The Bayesian Geometry of Transformer Attention" (Aggarwal et al., 27 Dec 2025)] and ["Gradient Dynamics of Attention: How Cross-Entropy Sculpts Bayesian Manifolds" (Aggarwal et al., 27 Dec 2025)]. Unlike these, which frame EM-like behavior as an analogy, the present analysis shows EM to be a deterministic consequence of objective geometry.

The theoretical connection to classical energy-based models, EM algorithms, and Mixture of Experts is clarified, with the key difference being the emergence of gating (responsibility) structure from loss and optimization—without explicit gating modules.

Limitations and Boundaries

The analysis holds for objectives with exponentiated distances and global normalization; it does not encompass multi-label situations, objectives lacking normalization (where responsibilities lose probabilistic meaning), or settings where prototype volumes (covariances) must be dynamically managed to avoid collapse. The connection to generalization, scaling, and emergent out-of-distribution behaviors is outside the scope of this framework.

Moreover, the framework does not explain why or when emergent capabilities appear at scale, nor does it model the effects of regularization techniques (norm constraints, weight decay, normalization layers), which are critical in practice to avoid degeneracies not controlled by the analyzed objectives.

Future Directions

The analysis suggests routes for objective refinement—such as explicit incorporation of volume penalties akin to log-determinants, or the design of open-set objectives that allow for "none-of-the-above" responsibility. It also motivates diagnostic tools for measuring implicit responsibilities via gradient traces during training, and for tracking specialization and collapse phenomena.

Extension to semi-supervised and probabilistically-labeled regimes offers a path to unify more complex training setups with the implicit EM perspective.

Conclusion

This work establishes that, for distance-based neural objectives of log-sum-exp form, the gradient with respect to each distance is exactly the negative responsibility of that component, unifying optimization and inference. EM is not an optional or emergent behavior in such systems—it is a necessary, mechanistic consequence of the loss and optimization geometry. This result provides both conceptual clarity and practical guidance for the understanding and design of neural architectures that operate on normalized, distance-based objectives.

Reference: "Gradient Descent as Implicit EM in Distance-Based Neural Models" (2512.24780)