Attention Is Not What You Need (2512.19428v1)

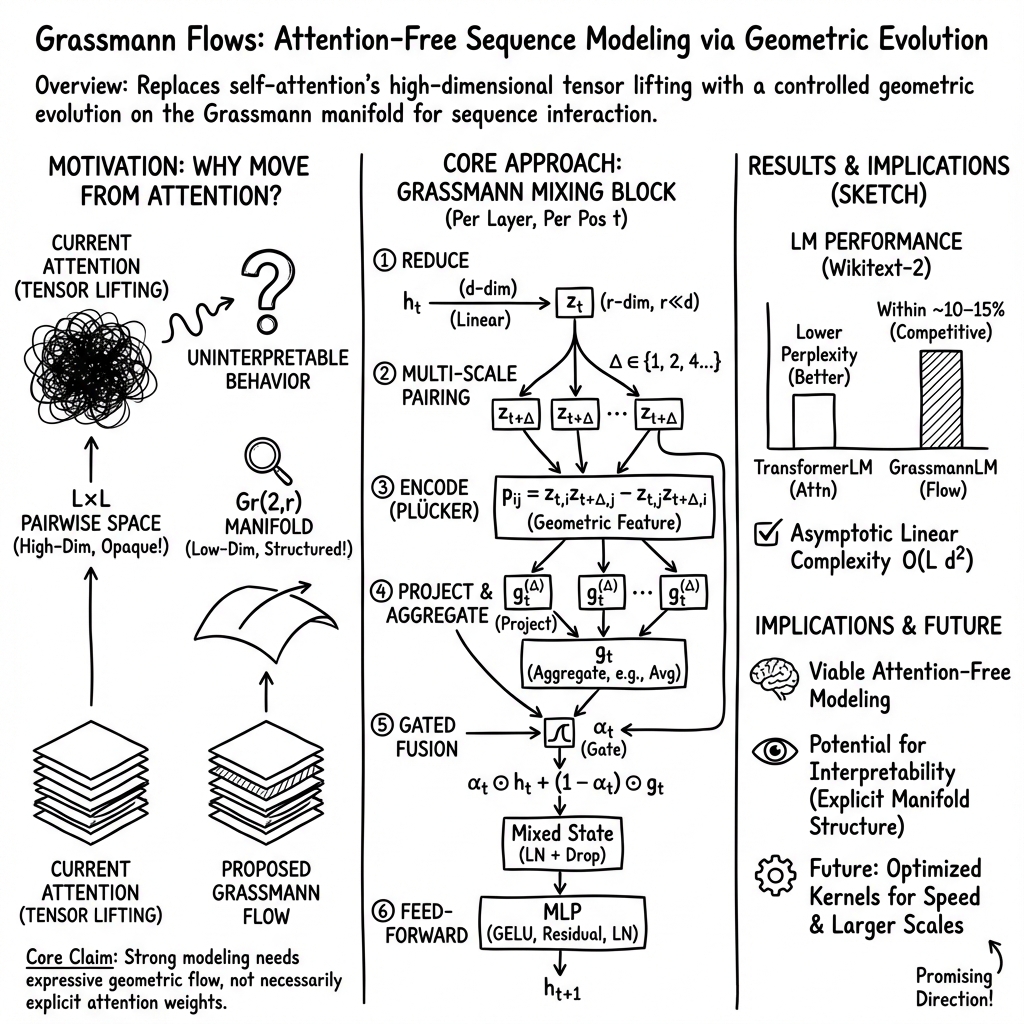
Abstract: We revisit a basic question in sequence modeling: is explicit self-attention actually necessary for strong performance and reasoning? We argue that standard multi-head attention is best seen as a form of tensor lifting: hidden vectors are mapped into a high-dimensional space of pairwise interactions, and learning proceeds by constraining this lifted tensor through gradient descent. This mechanism is extremely expressive but mathematically opaque, because after many layers it becomes very hard to describe the model with a small family of explicit invariants. To explore an alternative, we propose an attention-free architecture based on Grassmann flows. Instead of forming an L by L attention matrix, our Causal Grassmann layer (i) linearly reduces token states, (ii) encodes local token pairs as two-dimensional subspaces on a Grassmann manifold via Plucker coordinates, and (iii) fuses these geometric features back into the hidden states through gated mixing. Information therefore propagates by controlled deformations of low-rank subspaces over multi-scale local windows, so the core computation lives on a finite-dimensional manifold rather than in an unstructured tensor space. On the Wikitext-2 language modeling benchmark, purely Grassmann-based models with 13 to 18 million parameters achieve validation perplexities within about 10 to 15 percent of size-matched Transformers. On the SNLI natural language inference task, a Grassmann-Plucker head on top of DistilBERT slightly outperforms a Transformer head, with best validation and test accuracies of 0.8550 and 0.8538 compared to 0.8545 and 0.8511. We analyze the complexity of Grassmann mixing, show linear scaling in sequence length for fixed rank, and argue that such manifold-based designs offer a more structured route toward geometric and invariant-based interpretations of neural reasoning.

• The paper shows that sequence modeling can forgo explicit self-attention by employing Grassmann flows as a geometric evolution mechanism.
• It introduces the Causal Grassmann Transformer, which uses local pairwise subspace embeddings and Plücker coordinates to fuse token representations.
• Empirical results on language modeling and natural language inference demonstrate competitive performance and improved scalability compared to traditional attention models.

Summary of "Attention Is Not What You Need: Grassmann Flows as an Attention-Free Alternative for Sequence Modeling" (2512.19428)

Conceptual Motivation and Critique of Attention

The paper challenges the entrenched assumption that self-attention mechanisms are indispensable for strong sequence modeling in NLP. By reinterpreting self-attention as an instance of tensor lifting—where token representations are mapped into a high-dimensional space encoding explicit pairwise interactions—the author identifies the mathematical intractability of such lifted tensor spaces as a foundational source of Transformer uninterpretability. Specifically, the exponential growth of degrees of freedom across layers and heads renders concise, global invariants elusive, complicating both theoretical analysis and interpretability.

The proposed philosophical shift is to decenter attention: the essential ingredient for semantic reasoning is not attention per se, but a sufficiently expressive geometric evolution mechanism for hidden representations. The paper advances the view that geometric flows, with controlled algebraic and topological structure, can serve as viable alternatives, potentially making models more amenable to analytic scrutiny and facilitating the definition of explicit invariants.

Grassmann Flows: Architecture and Mathematical Underpinnings

The main technical contribution is the introduction of a fully attention-free sequence model, termed the Causal Grassmann Transformer, built around Grassmann flows. The core construction comprises:

1. Dimensionality Reduction: Token states $h_t \in \mathbb{R}^d$ are linearly projected to $z_t \in \mathbb{R}^r$ ($r \ll d$).
2. Local Pairwise Subspaces: Within local windows, pairs $(z_t, z_{t+\Delta})$ are treated as 2D subspaces on the Grassmann manifold $Gr(2,r)$.
3. Plücker Embedding: These subspaces are mapped via Plücker coordinates to a space of dimension $\binom{r}{2}$, encoding the algebraic structure of the underlying subspace.
4. Gated Fusion: Projected Grassmann features are fused back into token states through a gating mechanism, followed by standard feed-forward processing.

The architecture guarantees that global interactions are mediated via composition of local geometric flows rather than explicit $L\times L$ attention matrices, thus enforcing a finite-dimensional and algebraically structured trajectory in feature space.

Empirical Results and Complexity Analysis

Language Modeling (Wikitext-2)

Grassmann-based models with 13–18M parameters achieve validation perplexities consistently within 10–15% of size-matched Transformer baselines. Deeper architectures (12 layers) narrow this gap, indicating that an increase in depth compensates for local mixing limitations. This demonstrates that explicit attention matrices are not strictly necessary for competitive next-token prediction, provided that adequate geometric expressiveness is achieved via Grassmann flows.

Natural Language Inference (SNLI)

A Grassmann-based classification head appended to a fixed DistilBERT backbone slightly outperforms a Transformer head (val/test accuracy: 0.8550/0.8538 vs. 0.8545/0.8511). This result substantiates the claim that introducing explicit geometric structure into the mixing operation can yield competitive or superior downstream performance even in reasoning-intensive tasks.

Computational Scalability

The Causal Grassmann layer exhibits $\mathcal{O}(L)$ scaling in sequence length for fixed reduced dimension and window set, in contrast to the $\mathcal{O}(L^2)$ complexity of full self-attention. While current implementations are not yet faster than optimized attention kernels, the theoretical scaling advantage presents a pathway for handling long sequences efficiently, contingent upon engineering developments.

Interpretability and Theoretical Implications

A salient theoretical implication is the shift from opaque tensor lifting to controlled flows on structured manifolds. Grassmann flows provide algebraically constrained, finite-dimensional features (Plücker coordinates) that are comparable across layers, facilitating the definition and computation of global invariants—a prospect largely infeasible with dense attention tensors. This geometric compressibility opens avenues for invariant-based interpretability and geometric analysis of model dynamics, aligning more closely with differential and algebraic geometric tools.

Importantly, the architecture's universality is retained—neural networks remain theoretically capable of universal approximation on manifold-induced operators—but the imposed geometric prior governs the nature of information aggregation, potentially enhancing interpretability and analytic tractability.

Broader Impact and Connections

The work situates itself orthogonally to approaches that approximate or sparsify attention, demonstrating a distinct modeling regime where local geometric structure supplants global tensor interactions. The architectural bias towards structure and locality offers conceptual synergy with state-space models, and future research may exploit hybrid designs that integrate manifold flows with temporal dynamics.

In the context of non-Euclidean representation learning, the paper foregrounds the role of Grassmannians—a classic construct in geometry and subspace learning—as a primary mixing mechanism, expanding the toolkit for geometric reasoning in neural sequence modeling.

Prospects for Future Work

Promising directions include:

• Global Grassmannian Invariants: Defining and leveraging global statistical or topological descriptors (e.g., averaged subspaces, cross-layer stability measures) to enhance reasoning over long contexts.
• Higher-Dimensional Flows: Extending to $Gr(k,r)$ for $k>2$ and regularizing trajectories on the manifold, potentially increasing expressive power and flexibility.
• Geometric/Hybrid Models: Combining Grassmann flows with state-space, convolutional, or kernelized attention modules for richer multi-scale aggregation.
• Scalable Engineering: Implementing specialized GPU primitives for Grassmann operations to realize theoretical linear scaling at larger sequence lengths.
• Interpretability Analysis: Systematic investigation of the correlation between Plücker features and functional/effective reasoning in model predictions.

Conclusion

The paper decisively demonstrates that self-attention is not strictly necessary for effective sequence modeling in neural networks. Grassmann flows enable a fully attention-free alternative, preserving competitive performance through explicit geometric evolution mechanisms. This reorientation towards manifold-based operations opens substantial theoretical and practical opportunities, particularly in enhancing computational efficiency and interpretability for future neural architectures.