How Many Heads Make an SSM? A Unified Framework for Attention and State Space Models (2512.15115v1)

Abstract: Sequence modeling has produced diverse architectures -- from classical recurrent neural networks to modern Transformers and state space models (SSMs) -- yet a unified theoretical understanding of expressivity and trainability trade-offs remains limited. We introduce a unified framework that represents a broad class of sequence maps via an input-dependent effective interaction operator $W_{ij}(X)$, making explicit two recurring construction patterns: (i) the Unified Factorized Framework (Explicit) (attention-style mixing), in which $W_{ij}(X)$ varies through scalar coefficients applied to shared value maps, and (ii) Structured Dynamics (Implicit) (state-space recurrences), in which $W_{ij}$ is induced by a latent dynamical system. Using this framework, we derive three theoretical results. First, we establish the Interaction Rank Gap: models in the Unified Factorized Framework, such as single-head attention, are constrained to a low-dimensional operator span and cannot represent certain structured dynamical maps. Second, we prove an Equivalence (Head-Count) Theorem showing that, within our multi-head factorized class, representing a linear SSM whose lag operators span a $k$-dimensional subspace on length-$n$ sequences requires and is achievable with $H=k$ heads. Third, we prove a Gradient Highway Result, showing that attention layers admit inputs with distance-independent gradient paths, whereas stable linear dynamics exhibit distance-dependent gradient attenuation. Together, these results formalize a fundamental trade-off between algebraic expressivity (interaction/operator span) and long-range gradient propagation, providing theoretical grounding for modern sequence architecture design.

• The paper introduces the Interaction Rank Gap, showing single-head attention models are strictly less expressive than high-rank SSMs.
• It proves that multi-head attention can exactly emulate linear SSMs when the number of heads meets the interaction rank, linking head count to model capacity.
• The analysis reveals that attention mechanisms provide superior gradient flow for long-range dependencies, informing the design of effective hybrid architectures.

Unified Sequence Modeling: Attention and State Space Models

Introduction

The paper "How Many Heads Make an SSM? A Unified Framework for Attention and State Space Models" (2512.15115) presents a formal algebraic lens on sequence modeling architectures, encompassing Multi-Head Attention/Transformer variants, State Space Models (SSMs), convolutional structures, and more. The manuscript establishes a precise framework for quantifying the expressivity (via a notion termed "interaction rank") and trainability (via gradient flow analysis) of these architectures. Notably, it rigorously answers questions about the algebraic necessity of multiple attention heads and the trade-offs compared to SSM recurrence.

Unified Framework for Sequence Maps

The core formalism unifies explicit and implicit sequence models by representing the transformation from input $X \in \mathbb{R}^{d \times n}$ to output $Y \in \mathbb{R}^{p \times n}$ via an input-dependent effective weight tensor $W_{ij}(X)$. Architectures differ by their strategies for parameterizing $W_{ij}$:

• Explicit (Factorized) Models: Token-to-token mixing via attention mechanisms, where $W_{ij}(X) = f_\theta(x_i, x_j) V$ is rank-1 for scalar $f_\theta$ and shared value matrix $V$.
• Implicit (Structured Dynamics) Models: Recurrence-induced mixing via dynamical systems, where $W_{ij}$ is constructed by state evolution and can be full-rank.

This formulation is shown to encompass feedforward layers, CNNs, RNNs, SSMs, KANs, and all major softmax/linear attention variants.

Algebraic Analysis: Interaction Rank Gap

A central theoretical contribution is the Interaction Rank Gap. The paper proves that single-head (rank-1 factorized) attention models are strictly weaker than general linear SSMs with respect to the complexity of representable interaction operators:

• Single-head attention can only span a one-dimensional subspace in operator space, with $W_{ij}(X)$ a scalar multiple of a shared $V$.
• Linear SSMs can induce $W_{ij}$ that spans up to $k$ independent directions, where $k$ is the interaction rank determined by the system matrices $C\bar{A}^{\tau}\bar{B}$.

This is formalized by a uniform approximation lower bound: No single-head factorized model can uniformly approximate an SSM whose operators are not collinear, regardless of sequence length.

Figure 1: Test MSE versus the number of heads for different interaction ranks $k$; error sharply drops as head count $H$ matches $k$.

Numerically, the experiments show a sudden reduction in error only when the number of attention heads equals the target interaction rank $k$, consistent with the Head-Count Equivalence theorem.

Multi-Head Attention: Exact SSM Emulation

To bridge the expressivity gap, the paper proves an Equivalence (Head-Count) Theorem:

• For linear SSMs with interaction rank $k$, a multi-head factorized attention model can exactly represent the SSM if and only if the number of heads $H \geq k$. Each head corresponds to an independent basis matrix in operator space.
• The construction is explicit, showing how positional encodings and value matrices enable a causal attention layer to reproduce any linear SSM over finite sequences.

This result fundamentally connects the attention head count to the algebraic capacity of the architecture, rendering multi-head mechanisms necessary for emulating richer dynamical systems.

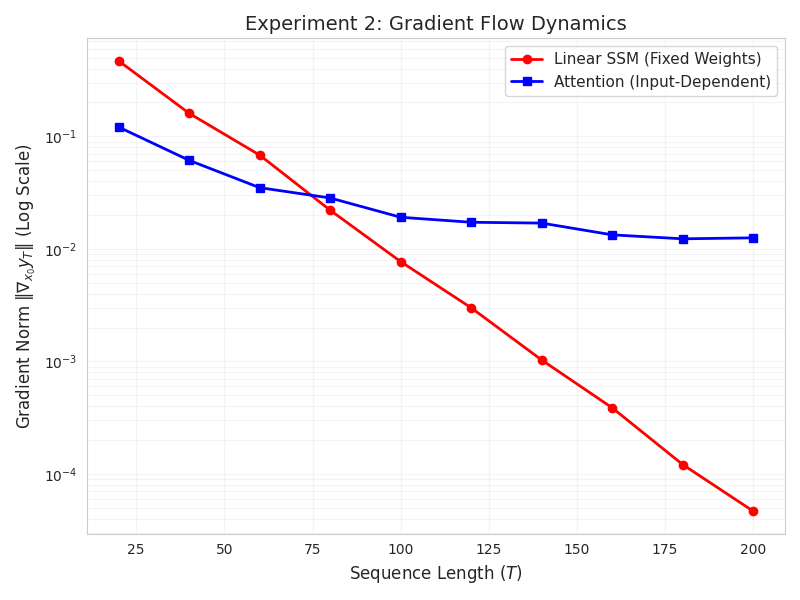
Gradient Flow and Long-Range Trainability

The manuscript rigorously studies optimization properties, focusing on the attenuation of gradients with respect to sequence distance:

• Linear SSMs: Jacobian norms between distant time steps decay exponentially for stable system matrices ($\|\bar{A}\|_2 < 1$), causing vanishing gradients and hindering optimization of long-range dependencies.
• Attention: The framework proves that the Jacobian path from output to input can be distance-invariant for suitable input configurations—attention admits direct $O(1)$ "gradient highway" paths, enabling signal preservation independent of sequence distance.

  Figure 2: Gradient norm $\|\nabla_{x_0} y_T\|$ decays rapidly for SSMs but much slower for attention, showing superior long-range trainability.

Synthetic experiments corroborate these results, visualizing exponential gradient decay in SSMs versus sustained gradient norms in attention layers, explaining the empirical trainability advantages of attention architectures.

Practical Implications and Hybrid Design

The interaction rank and trainability analyses rationalize the emergence of hybrid architectures, such as Jamba, which interleave SSM blocks (high expressivity, efficient recurrence) with attention layers (long-range interaction, gradient preservation). Under the unified lens:

• SSM blocks capture high-rank state evolution efficiently.
• Attention blocks inject non-local operations to prevent gradient attenuation, complementing the SSM dynamics.

This principle guides the design of architectures balancing structured dynamical modeling and robust optimization for tasks requiring both expressivity and long-context modeling.

Theoretical Extensions

The sufficiency construction for multi-head attention matching SSMs is further refined under spectral assumptions on $\bar{A}$. Translation-invariant features with $O(mJ^2)$ dimension per head, where $m$ is the state size and $J$ the maximal Jordan block size, are sufficient for exact representation in common SSM parameterizations.

Conclusion

The algebraic framework presented establishes a precise hierarchy of sequence model expressivity and trainability. Multi-head attention mechanisms are algebraically essential to bridge the gap between attention and SSMs, with head count dictating interaction rank. Conversely, attention architectures offer intrinsic optimization benefits via gradient highways. These findings underpin the architectural choices being made in modern large-scale models and illuminate the fundamental trade-offs at play in sequence modeling. The work provides a principled foundation for the further development and rigorous analysis of hybrid and next-generation architectures in sequence learning.