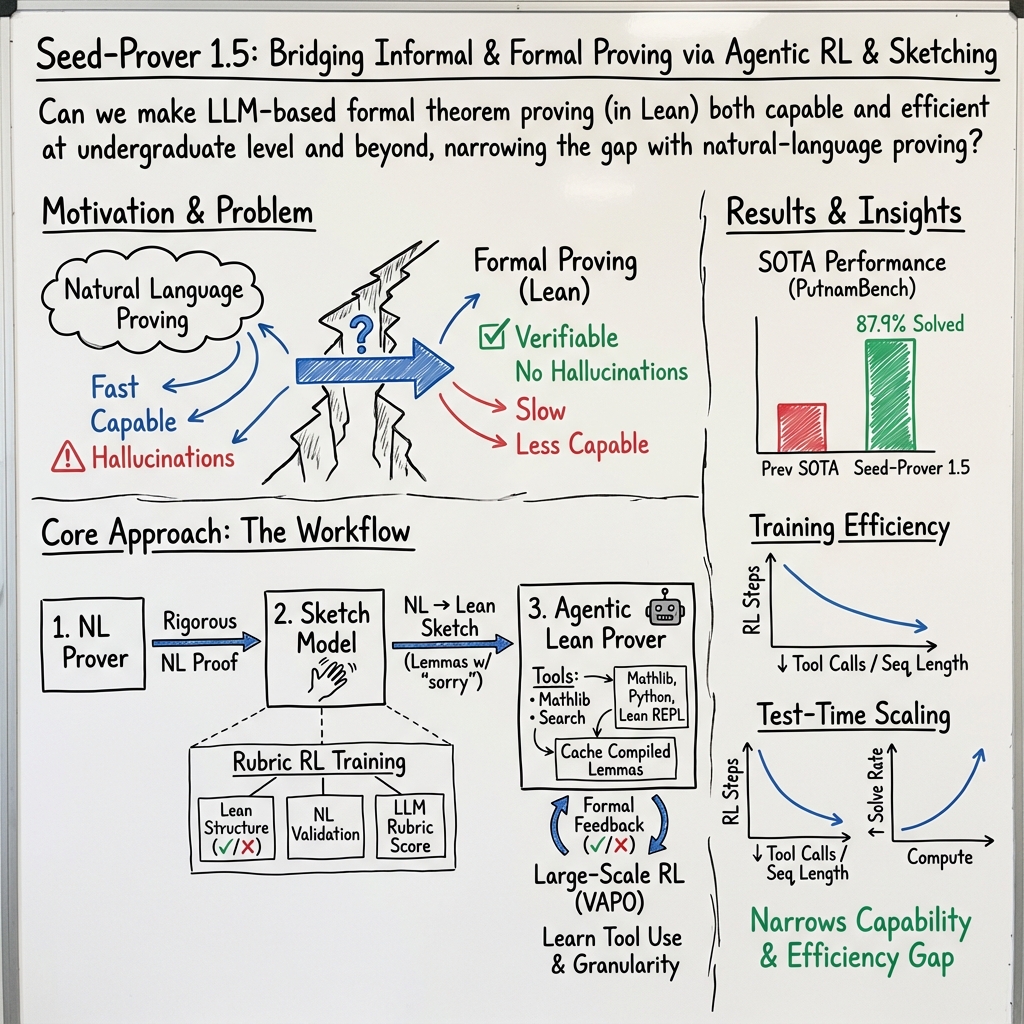
Seed-Prover 1.5: Mastering Undergraduate-Level Theorem Proving via Learning from Experience
Abstract: LLMs have recently made significant progress to generate rigorous mathematical proofs. In contrast, utilizing LLMs for theorem proving in formal languages (such as Lean) remains challenging and computationally expensive, particularly when addressing problems at the undergraduate level and beyond. In this work, we present \textbf{Seed-Prover 1.5}, a formal theorem-proving model trained via large-scale agentic reinforcement learning, alongside an efficient test-time scaling (TTS) workflow. Through extensive interactions with Lean and other tools, the model continuously accumulates experience during the RL process, substantially enhancing the capability and efficiency of formal theorem proving. Furthermore, leveraging recent advancements in natural language proving, our TTS workflow efficiently bridges the gap between natural and formal languages. Compared to state-of-the-art methods, Seed-Prover 1.5 achieves superior performance with a smaller compute budget. It solves \textbf{88\% of PutnamBench} (undergraduate-level), \textbf{80\% of Fate-H} (graduate-level), and \textbf{33\% of Fate-X} (PhD-level) problems. Notably, using our system, we solved \textbf{11 out of 12 problems} from Putnam 2025 within 9 hours. Our findings suggest that scaling learning from experience, driven by high-quality formal feedback, holds immense potential for the future of formal mathematical reasoning.
Summary
- The paper introduces a scalable agentic reinforcement learning framework that incrementally constructs proofs using modular lemma caching and adaptive tool invocation.
- It employs a hierarchical sketch model to seamlessly bridge natural language reasoning and formal Lean proofs for efficient inference.
- The approach achieves up to 87.9% success on undergraduate benchmarks while reducing computational costs, demonstrating significant practical impact.
Seed-Prover 1.5: Agentic Reinforcement Learning for Formal Undergraduate-Level Theorem Proving
Introduction and Motivation
Formal mathematical reasoning using LLMs has remained a significant challenge, especially when targeting formal languages such as Lean, which demand both rigorous proof construction and computational efficiency. While recent advances in natural language mathematical reasoning have yielded near-perfect scores on undergraduate benchmarks, a substantial gap persists in capability and resource consumption between formal and informal approaches. Seed-Prover 1.5 directly addresses these limitations, introducing a scalable, agentic reinforcement learning framework with hierarchical decomposition and efficient inference for formal theorem proving at undergraduate and graduate levels.
Figure 1: Performance of Seed-Prover 1.5 compared to other state-of-the-art provers, demonstrating a substantial performance gain at reduced computational cost.
Agentic Prover Architecture and Training
Seed-Prover 1.5 employs a multi-tool, agentic RL paradigm distinct from prior step-level and whole-proof models. Rather than frequent interaction per tactic (inefficient context usage) or single-shot large proofs (sparse feedback), this agent incrementally constructs formal proofs via modular lemma caching and adaptive tool invocation (Lean verification, Mathlib semantic search, Python execution). This tuning allows efficient exploitation of Lean's verifiable environment and targeted RL, facilitating fine-grained learning from high-quality formal feedback.
Figure 2: An example trace of Seed-Prover 1.5's agentic strategy on a FATE-H problem, showcasing interleaved tool calls and efficient lemma caching.
Agentic prover training utilizes supervised fine-tuning on synthetic datasets followed by careful outcome-based RL leveraging VAPO for stable optimization. Training examples are curated to maximize challenge and learning signal, selectively filtering for hard instances through multi-pass model evaluation and self-summarization. The reward is binary, strictly reflecting Lean-verified proof success, and the RL process interleaves multi-turn tool interactions within long context windows for maximal expressivity.
Post-Training Dynamics and Efficiency
Extensive RL training yields significant improvements in proof accuracy and tool-use efficiency. Batch-level training accuracy approaches 90%, and the average number of function/tool calls per proof trajectory drops sharply, indicating the agent's ability to synthesize and optimize reasoning procedures adaptively.
Figure 3: Batch-level training accuracy increases sharply after RL, reflecting improved learning signal extraction and higher formal proving rates.
Figure 4: The average number of function calls per proof decreases over RL steps, evidencing more strategic and less redundant tool invocation.
Adaptive behavior emerges: on tool-intensive datasets (e.g., FATE-H), the agent increases Mathlib usage; on others (Putnam), reliance is reduced, reflecting successful knowledge internalization and search simplification.
Hierarchical Sketch Model and Decomposition
To further leverage recent gains in natural language reasoning, Seed-Prover 1.5 introduces a sketch model that bridges NL proofs and formal Lean decomposition. The sketch agent, trained via Rubric RL and VAPO with hybrid compiler-LLM-as-judge rewards, generates lemma-based Lean templates, which are then processed as parallelizable sub-goals for the formal prover.
Figure 5: An example sketch generated by Seed-Prover 1.5, illustrating decomposition into auxiliary lemmas and a structured main proof body.
Quality is strictly assessed with binary rewards that force sufficient decomposition, lemma correctness, and alignment with NL guidance, validated via targeted rubric and NL disproof checks. This enables efficient hierarchical expansion at inference (test time), leading to robust scaling on complex proofs.
Test-Time Scaling and Benchmark Results
Seed-Prover 1.5 orchestrates three collaborating agents: NL Prover, Sketch Model, and Agentic Lean Prover. Given a Lean statement, proofs are initiated in natural language, converted to Lean sketches, and recursively decomposed into lemma-level sub-proofs. This modular approach (employing pass@3×3 compute scaling) enables a log-linear increase in solved problems with increased computational budget, with most distribution clustered in early inference hours and a long tail for hardest cases.
Figure 6: Scaling of solved problems with compute; Seed-Prover 1.5 solves problems on PutnamBench with log-linear scaling in computational budget.
Across competitive benchmarks:
- PutnamBench (Undergraduate): 87.9% solved, outperforming AlphaProof, Hilbert, and Aleph Prover under dramatically lower compute budgets.
- FATE-H (Graduate): 80% solved.
- FATE-X (PhD-level): 33% solved, highlighting limitations due to increased mathematical complexity and Mathlib coverage gaps.
Figure 7: Visualization of Seed-Prover 1.5's capability on the Putnam benchmark, indicating high proficiency on undergraduate problems.
Seed-Prover 1.5 demonstrated the ability to solve 11 out of 12 Putnam 2025 competition problems within a 9-hour window and matched state-of-the-art human-expert performance on selected IMO 2025 problems using reduced inference budgets.
Practical and Theoretical Implications
Practically, Seed-Prover 1.5 narrows the gap between formal and informal proving efficiency at undergraduate/graduate levels, making formal verification of significant mathematical exercises tractable on modest resources. Its agentic RL methodology and modular workflow enable both fast development and extensibility, providing a robust blueprint for scalable, formalized proof automation.
Theoretically, the work substantiates that extensive learning from experience—driven by high-quality, ground-truth formal feedback—can yield substantial advances in formal mathematical reasoning. Yet, it exposes limitations at higher complexity tiers due to Mathlib coverage and proves relatively simple or mis-formalized frontier problems but falls short of driving independent mathematical research comparable to expert human synthesis.
Future Directions
Seed-Prover 1.5's limitations on PhD-level and open conjectures underscore three bottlenecks for future progress:
- Automatic identification and formalization of influential research papers.
- Natural language reasoning grounded in state-of-the-art mathematics.
- Scalable formalization of both referenced results and newly derived insights.
Solving these would enable large-scale formal mathematical research and potentially contribute to resolving open conjectures using automated agents.
Conclusion
Seed-Prover 1.5 presents an agentic RL system integrating hierarchical sketch-driven decomposition for formal theorem proving at undergraduate and graduate levels. Its empirical results validate the efficacy of learning from experience in verifiable environments, bridging much of the capability gap between formal and informal mathematical reasoning. While significant challenges remain—especially at the frontier of mathematical knowledge—the system offers a scalable paradigm and foundational architecture for future advances in AI-driven formal mathematics.
Whiteboard
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
Overview
This paper introduces Seed‑Prover 1.5, an AI system that writes and checks math proofs in a computer language called Lean. Lean is strict: it won’t accept a proof unless every step is correct. The goal is to make AI good at “formal theorem proving” (proving math in Lean), not just writing nice-sounding proofs in everyday English. Seed‑Prover 1.5 learns by practicing thousands of times with real feedback and uses a smart workflow that breaks big problems into smaller parts so it can solve tough, university-level math problems efficiently.
What questions does the paper try to answer?
The paper focuses on three simple questions:
- Can we train an AI to prove math theorems in Lean more effectively by letting it learn from experience?
- Can we use strong English-language proofs to guide and speed up formal proofs in Lean?
- Can we solve hard math problems (like those in the Putnam and graduate-level exams) with less computing power than previous systems?
How does the system work?
To understand the approach, think of the AI like a student solving a big math problem with tools and a coach:
- Lean is the coach who checks every step and says “correct” or “wrong.”
- “Mathlib” is a large math library—the student’s textbook of known facts and theorems.
- The AI student uses multiple tools and a plan to get the job done.
Here are the main ideas, explained with everyday language:
- Agentic Prover: Instead of writing the entire proof in one go, the AI writes it piece by piece using “lemmas” (small helpful steps). It sends each lemma to Lean to check. Once Lean approves a lemma, the AI saves it and reuses it later—just like keeping finished Lego blocks to build a bigger structure. This makes the process faster and more organized.
- Tool Use:
- Lean verification: The AI asks Lean to check each lemma and returns structured feedback (“this step works” or “this part fails”).
- Mathlib search: The AI looks up relevant theorems by meaning, not just keywords—like searching a textbook by the idea you need.
- Python execution: For some problems, the AI can run quick number checks or experiments to guide its thinking.
- Learning from Experience (Reinforcement Learning): The AI practices proving many problems. When it finishes a correct proof, it gets a “point” (reward = +1). If it fails, it gets a penalty (reward = −1). Over time, it figures out better strategies—like which tools to use, when to search, and how to split problems into easier parts.
- Sketch Model (Bridge from English to Lean): The system trains another AI to read a natural-language proof (in English) and turn it into a Lean “sketch”: a plan with multiple lemmas. At first, these lemmas may be marked “sorry” (meaning “to be proved later”), but they provide a clear roadmap. A separate “judge” model checks if each lemma makes sense and matches the English proof.
- Test-Time Workflow (Solving process): For a new problem, the system:
- Writes a careful English proof.
- Converts that proof into a Lean sketch with lemmas.
- Proves each lemma one by one in Lean, reusing verified parts. If a lemma is too hard, it breaks it down further. If a lemma is wrong, it refines the sketch. This repeats until all lemmas are proved or the time limit is reached. Think of this like exploring a maze: try a path, save progress, backtrack if needed, and split the maze into rooms.
What did they find?
Here are the main results, and why they matter:
Strong performance with less compute:
- PutnamBench (undergraduate level): solved about 88% of problems.
- Fate-H (graduate level): solved about 80%.
- Fate-X (PhD level): solved about 33%.
- These are better or competitive with other leading systems, but with a smaller computing budget. That’s important because it makes the approach more practical and scalable.
- Real-world tests:
- Putnam 2025: the system solved 11 out of 12 problems within 9 hours.
- IMO 2025: solved 5 out of 6 problems under a reasonable compute setting.
- Learning improvements:
- During training, the AI got more accurate and used fewer tool calls and shorter proofs—meaning it learned to be more efficient, not just more powerful.
- Bridging English and Lean works:
- Using the sketch model, the system effectively turned strong English proofs into formal Lean plans, then verified every detail. This “bridge” greatly sped up formal proving.
- Limits:
- PhD-level problems are still tough. Some areas depend on missing pieces in Mathlib or require deep knowledge from research papers, which are harder to formalize.
Why does this matter?
This research shows that formal theorem proving with AI is becoming both powerful and efficient. It proves that:
- Learning from strict feedback (Lean’s checks) helps AI build trustworthy math proofs.
- Combining natural-language reasoning with formal verification speeds up solving hard problems.
- Breaking big problems into smaller lemmas and caching verified pieces is a smart strategy that saves time and compute.
In the long run, this could help mathematicians check complex proofs, teach students with reliable step-by-step solutions, and maybe even contribute to tackling advanced open problems—once we can better connect formal tools to the huge landscape of research papers. For now, Seed‑Prover 1.5 is a strong step toward AI systems that reason carefully, prove rigorously, and do so efficiently.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise, actionable list of what remains missing, uncertain, or unexplored in the paper.
- Lack of principled, sound lemma validation for the sketch model: the paper uses an NL prover and LLM-as-judge rubric (with a 0.7 threshold) to accept/reject lemmas, but does not quantify false-positive/false-negative rates or provide guarantees against subtle mathematical errors in lemma statements.
- Unclear robustness of the rubric reward: no ablation comparing rubric-driven rewards vs. scalar learned value models, self-consistency scoring, or formal-checkable proxies; sensitivity to rubric prompt design and judge model choice is not analyzed.
- No auditing of “difficulty reduction”: the claim that the sketch makes the hardest lemma strictly easier is enforced only by rubric heuristics; there is no quantitative measure (e.g., empirical hardness proxies, solution time, or formal complexity metrics) validating true difficulty reduction.
- Potential unsoundness from Python tool-use: the agent uses Python execution for numerical checks, but safeguards against floating-point errors, random seeds, non-determinism, or spurious empirical validation are not described.
- Limited error analysis of failures on Fate-X and other hard instances: no breakdown of dominant failure modes (e.g., missing Mathlib facts, decomposition errors, search horizon limits, tactic synthesis failures, wrong lemma statements).
- No ablation of tool categories: the contribution of Mathlib retrieval vs. Lean verification vs. Python execution to final solve rates and efficiency is not quantified.
- Missing ablation of agentic granularity: there is no systematic study comparing lemma-level interaction against step-level and whole-proof paradigms under matched compute budgets.
- Sparse analysis of search hyperparameters: the effects of maximum tool calls, maximum sequence length, search width/depth, and backtracking heuristics on performance and cost are not reported beyond a single setting.
- Open question on lemma caching scope: it is unclear whether cached lemmas are local to a problem, session, or global library; the risks of reusing overly-specific or environment-dependent lemmas are not analyzed.
- Limited exploration of long-context reasoning: the paper notes degraded scores at 32k–64k tokens, but provides no methods (e.g., state summarization, retrieval-augmented memory, structured proof state encoding) to reliably scale beyond these ranges.
- RL reward design is minimal: binary +1/−1 outcome rewards omit efficiency, tool-use cost, lemma reuse, or decomposition quality; the impact of richer reward shaping or multi-objective RL is not explored.
- Credit assignment across tool calls: how advantages are estimated and assigned in multi-turn, tool-interleaved rollouts (VAPO) is not detailed; no ablation on off-policy/on-policy data mixing or tool-call credit propagation is given.
- Missing RL hyperparameters and training details: clipping ranges (, ), learning rates, KL control, update frequency, and baselines are not reported; the PPO equation is mis-typeset, hampering reproducibility.
- Dataset filtering introduces bias: excluding problems the SFT model solves >3 times may skew training toward hard tails; no analysis of catastrophic forgetting on “easy” cases or overall calibration drift is provided.
- In-house data opacity: the “in-house formalized math textbooks” (e.g., GTM) are not released or described in detail; contamination checks and licensing status are unclear; this blocks reproducibility and fair comparison.
- Generalization across Mathlib versions: the system is pinned to Mathlib v4.22.0; robustness to library updates, API churn, and theorem renaming/restructuring is untested.
- Retrieval quality and coverage: retrieval recalls/precision for Mathlib search and its failure cases (e.g., synonyms, notational variance) are not measured; no learning-to-retrieve or interactive retrieval refinement is presented.
- Fair compute comparisons: “H20-days/problem” is not defined in FLOPs, wall-clock, or energy; comparisons to baselines (e.g., TPU-days, pass@k) are not normalized, making “smaller compute budget” claims hard to verify.
- Limited evaluation diversity: performance is reported mainly on Putnam/FATE; broader coverage (Isabelle/Coq ecosystems, non-olympiad domains, algebraic geometry/analysis-heavy tasks) is absent.
- Limited analysis of combinatorics and new-definition synthesis: the system struggles with datasets like CombiBench due to formalization issues; no targeted method for on-the-fly definition creation, schema induction, or “definition debugging” is proposed.
- Missing component-level ablations for the test-time workflow: the incremental gains from NL prover, sketch model, and agentic prover (and their failure handoffs) are not isolated.
- No study of recursive decomposition depth: although max depth is capped at 4 (with restart to 8), there is no analysis of optimal depth/width policies, learned search control, or completeness/soundness trade-offs of the recursive strategy.
- No comparison to MCTS/BFS at the lemma level: whether lemma-level MCTS or best-first search outperforms the current heuristic orchestration remains unknown.
- Safety constraints in Lean tactics: beyond avoiding
native_decide, the paper does not enumerate other potentially unsafe tactics or settings and how they are mitigated at scale. - Limited treatment of proof maintainability: metrics for proof readability, refactoring cost, tactic stability, and brittleness under library changes are not reported.
- Robustness to adversarial or subtly wrong NL proofs: the system relies on NL proofs to seed sketches; how it reacts to misleading or incomplete NL arguments is not evaluated.
- Distribution shift in the rubric judge: the LLM judge itself may be biased or fail on out-of-domain topics; calibration and consistency checks for the judge over time are absent.
- Lack of novelty detection and formalization fidelity: in Erdős cases, the paper notes trivial or simplified versions being proved due to mis-formalization; there is no systematic method to detect under-specification or over-simplification of problem statements.
- No integration with literature-grounded proving: the “dependency issue” (using multiple research papers) is identified but no concrete pipeline for paper retrieval, citation graph navigation, and formalization of referenced results is proposed.
- Library growth and knowledge consolidation: unlike LEGO-style approaches, the system does not study how to curate, generalize, and re-export newly proved lemmas into a reusable, evolving library with quality control.
- Limited cross-assistant portability: applicability to Coq, Isabelle, or HOL Light, and the portability of the agentic strategies and sketch interface, are not investigated.
- Insufficient transparency on base model: details on the underlying model size, pretraining corpus, and safety filters are missing; contributions of base capabilities vs. RL fine-tuning cannot be disentangled.
- No systematic data leakage assessment: while IMO/Putnam 2025 are said to be leak-free, comprehensive leakage audits for PutnamBench/FATE and in-house data (e.g., overlapping problem statements/solutions) are not documented.
- Lack of persistence/memory across problems: the system proves lemmas per problem but does not maintain a long-term memory of reusable results or learned tactics; strategies for lifelong learning remain unexplored.
- Economic and energy cost: end-to-end costs (training and inference) are not reported in standardized units; the cost–quality trade-off curves and carbon footprint are unknown.
- Security of tool-use: executing generated Python code poses security risks; sandboxing, resource limits, and audit logs are not described.
- Human-in-the-loop opportunities: the paper does not study when minimal expert hints (definitions, key lemmata) most improve success per unit cost, or design low-latency interfaces to solicit such input.
- Benchmarks with formalization ambiguity: strategies for detecting and repairing dataset misformalizations (e.g., automatic counterexample finding, spec mining, proof repair) are not integrated into the pipeline.
- Theoretical understanding of agentic RL: there is no analysis of convergence, sample efficiency, or guarantees for learning tool-use policies in environments with sparse but high-fidelity rewards like Lean.
Practical Applications
Immediate Applications
Below are concrete, deployable use cases that can leverage Seed-Prover 1.5’s agentic Lean prover, sketch model, and test-time scaling workflow now, together with sector links, plausible tools/products, and feasibility notes.
- Formal-proof copilot for mathematicians and proof engineers (Academia, Software)
- What: Assist Lean users with lemma decomposition, Mathlib search, and incremental proof construction with cached lemmas.
- Tools/Products: VS Code/Lean plugin “Proof Copilot”; PR bot for Lean repos that suggests lemmas and repairs; context-window–efficient proof sessions.
- Dependencies/Assumptions: Lean v4.22.0 pin; Mathlib coverage; moderate compute for Pass@k; team readiness to adopt Lean workflows.
- Auto-formalization assistant for courses and textbooks (Education)
- What: Convert natural-language solutions to Lean sketches (lemma-style proof outlines with sorry-admitted subgoals) for teaching, homework, and exams.
- Tools/Products: LMS plugin for “Sketch-to-Lean”; autograder that checks student-filled lemmas; instructor dashboard for hint generation and difficulty calibration.
- Dependencies/Assumptions: Course content formalizable in Mathlib; faculty and TA adoption; sandboxed compute per assignment; alignment with academic integrity policies.
- Continuous integration (CI) for formal math libraries (Academia, Open Source)
- What: On pull requests, the agent runs light inference to complete small gaps, check regressions, suggest minimal patches, and detect brittle proofs.
- Tools/Products: “Lean CI Prover” GitHub App; regression dashboard with proof-length and tool-call metrics; automated lemma search and refactor suggestions.
- Dependencies/Assumptions: Stable CI runners with Lean toolchain; Mathlib commit pinning; compute budget preconfigured; contributor consent to automated edits.
- Proof-of-correctness for algorithmic kernels and scientific code (Software, ML Infra, Energy/Scientific Computing)
- What: Prove properties like termination, convexity, bounds, invariants, and numerical safety for core algorithms (optimizers, solvers).
- Tools/Products: “Formal Kernel Verifier” that pairs specs (Lean theorems) with incremental proof attempts; Python-check tool for quick numerical sanity checks.
- Dependencies/Assumptions: Clear formal specs; feasibility of modeling algorithms in Lean; bridging floating-point vs exact math; engineering time to write specs.
- Smart contract and protocol verification accelerator (Blockchain, Security)
- What: Assist with high-level invariants and math-heavy components (e.g., tokenomics, AMM invariants, signature schemes) by generating lemma sketches and proofs.
- Tools/Products: Pipeline from contract spec → Lean sketch → formal lemma proofs; advisor that proposes invariants and checks them.
- Dependencies/Assumptions: Translation from contract languages to Lean specs; availability of crypto/math libraries; auditors comfortable with Lean artifacts.
- Cryptographic proof assistant (Security)
- What: Verify algebraic and number-theoretic lemmas underpinning proofs (e.g., group structure, hardness reductions) with mathlib-anchored search.
- Tools/Products: “Crypto-Math Lean Pack” templates; sketch model to decompose long reductions; proof caching for reusable lemmas across schemes.
- Dependencies/Assumptions: Adequate Mathlib support for algebra/number theory; domain experts to supervise formalization boundaries.
- Reproducible derivation checking for papers and technical docs (Academia, Industry R&D)
- What: Turn derivations in PDFs/notes into Lean sketches; agent verifies sub-lemmas; numerically probes claims with Python as a stopgap.
- Tools/Products: “ProofCheck for Docs” service; journal submission add-on validating lemma decomposition and linking to Lean artifacts.
- Dependencies/Assumptions: Tolerance for partial formalization; document-to-structured-text extraction; author willingness to refine specs.
- Competition training and coaching (Education)
- What: Generate structured hints, lemma plans, and verified subgoals for Putnam/IMO practice; autograde formal proofs.
- Tools/Products: “Putnam Coach” with scalable test-time search; skill analytics on decomposition and lemma difficulty.
- Dependencies/Assumptions: Compute quotas per user; alignment with contest rules for training; supervision to prevent overfitting specific styles.
- Verified analytics for finance math components (Finance)
- What: Prove identities, limit theorems, or risk aggregation properties in valuation/risk models where feasible in Lean.
- Tools/Products: “Quant Proof Kit” templates for pricing/hedging lemmas; CI check for model changes affecting invariants.
- Dependencies/Assumptions: Formalizable core math (measure/probability coverage in Mathlib); acceptable performance–formalization trade-offs.
- Knowledge graph of formal lemmas for enterprise reuse (Enterprise Knowledge Management)
- What: Leverage the agent’s lemma caching to build a searchable, provenance-tracked lemma graph for teams.
- Tools/Products: “Enterprise Math Atlas” with dependency visualization and reuse suggestions in proofs.
- Dependencies/Assumptions: Security policies for internal math; storage and indexing of formal artifacts; versioning across Lean commits.
- Tool-integrated RL with verifiable feedback for code and math (AI/ML Tooling)
- What: Apply Seed-Prover’s tool-use RL recipe (Lean verification, compilation feedback, pass@k workflows) to program synthesis and repair.
- Tools/Products: “Verifier-in-the-Loop RL” harness using compilers, test suites, and static analyzers as reward oracles.
- Dependencies/Assumptions: High-quality, fast oracles; careful reward design; cost control for tool calls; domain-specific datasets.
- Internal benchmarking and capability evaluation (AI Labs, QA)
- What: Use PutnamBench/FATE-like suites to track model and workflow improvements under fixed budgets and pass@k settings.
- Tools/Products: A/B testing harness with solve-rate vs compute curves, search-depth/width tuning dashboards.
- Dependencies/Assumptions: Dataset licensing; strict data hygiene to avoid leakage; reproducible environment pinning.
Long-Term Applications
The following use cases require further research, scaling, library expansion, or ecosystem agreement before widespread deployment.
- Autonomous research assistant for mathematics (Academia, AI4Science)
- What: Read papers, extract definitions/lemmas, build formal libraries, propose conjectures, and attempt proofs end-to-end.
- Emergent Workflow: Literature retrieval → NL proof drafting → sketch decomposition → iterative formalization → proof search with TTS scaling.
- Dependencies/Assumptions: Robust autoformalization of dense math texts; larger Mathlib coverage; reliable NL-to-formal alignment; persistent memory over large corpora.
- End-to-end formal verification for safety-critical systems (Aerospace, Automotive, Medical Devices, Robotics)
- What: Verify control/stability, scheduling, and safety invariants across software–hardware stacks; support certification (e.g., DO-178C).
- Tools/Products: Domain-specific libraries (control theory, numerical certs), Lean–C/LLVM bridges, obligation generators from specs.
- Dependencies/Assumptions: Industrial-grade interop (Coq/Isabelle/Lean); robust libraries for real analysis and control; regulator buy-in.
- Regulatory-grade financial model assurance (Finance, Policy)
- What: Require machine-checkable proofs for certain risk and capital models; provide audit trails with formal artifacts.
- Tools/Products: “Reg-Ready Proof Packs” and model change management tied to formal invariants; audit dashboards linking proofs to filings.
- Dependencies/Assumptions: Standards-setting by regulators; domain formal libraries (stochastic calculus); performance acceptable for production cycles.
- Formalized scientific publishing and peer review (Academia, Publishing)
- What: Journals accept or encourage formalized lemmas for key claims; reviewers use agents to probe decomposition quality and soundness.
- Tools/Products: Submission validators; archive of formal artifacts per paper; cross-paper lemma reuse detection.
- Dependencies/Assumptions: Community norms; authoring tools; incentives for authors and reviewers; stable archival infrastructure.
- Cross-system proof interoperability and standardization (Software Tooling)
- What: Reliable translation among Lean, Coq, Isabelle, and HOL; shared proof exchange formats and certification pipelines.
- Tools/Products: Proof translators with semantics-preserving guarantees; cross-system search over theorem libraries.
- Dependencies/Assumptions: Agreement on standards; bridging subtle logical differences; long-term maintenance.
- Legally reliable smart contracts and computable law (Policy, LegalTech, Blockchain)
- What: Translate legal clauses to formal semantics with proofs of compliance and dispute-handling properties; high-assurance smart contracts.
- Tools/Products: Domain-specific logics for law; “Legal-to-Formal” compilers; compliance provers tied to regulatory texts.
- Dependencies/Assumptions: Formal legal ontologies; acceptance in courts/regulators; human-in-the-loop drafting standards.
- LLM safety and reliability via verifiable feedback (AI Safety)
- What: Train general agents with ground-truth, executable or formal feedback (beyond math), reducing hallucinations and enabling scalable oversight.
- Tools/Products: RL harnesses with simulators, compilers, and checkers as rewards; rubric-based value models for semantics.
- Dependencies/Assumptions: High-fidelity environments for non-math tasks; cost-effective feedback loops; generalization of rubric RL beyond math.
- Formal analytics for critical infrastructure and energy systems (Energy, Operations Research)
- What: Verified optimization and scheduling models (grid dispatch, market clearing, resilience guarantees) with machine-checked obligations.
- Tools/Products: Lean libraries for OR/convex analysis; pipeline that turns planning specs into formal obligations and lemmas.
- Dependencies/Assumptions: Adequate modeling fidelity; scalability to industry-size instances; stakeholder adoption.
- Automated cryptographic protocol design and verification (Security)
- What: Agents propose protocols and jointly prove confidentiality/integrity/liveness properties under formal adversary models.
- Tools/Products: Libraries for simulation-based proofs, reductions, games; composable security frameworks in Lean.
- Dependencies/Assumptions: Mature crypto libraries; efficient automation for probabilistic reasoning; expert oversight.
- Scalable, fully autograded formal-proof curricula (Education at Scale)
- What: End-to-end formal coursework where every assignment is machine-checked; credentials rooted in verified proof portfolios.
- Tools/Products: Courseware generators; difficulty-adaptive hinting; personalized decomposition trajectories.
- Dependencies/Assumptions: Better UX for novices; institutional support; compute provisioning for cohorts.
- Enterprise knowledge OS of formalized results (Enterprise, R&D)
- What: A living, queryable repository of formalized models and results across teams, with lineage tracking and reuse.
- Tools/Products: Semantic search over lemma graphs; change-impact analysis; policy enforcement via formal obligations.
- Dependencies/Assumptions: Organization-wide formalization culture; integration with internal tooling; governance for updates.
- Verified ML pipelines and models (ML Infra, Safety-Critical AI)
- What: Prove properties of training procedures, loss landscapes (where possible), or post-training safety constraints; checkable logs for audits.
- Tools/Products: “Proof-aware” training frameworks; certified post-processing steps; formal specification of safety constraints.
- Dependencies/Assumptions: Feasibility of formalizing relevant ML math; acceptance of partial proofs; performance overheads.
Notes on general feasibility across applications:
- Scaling limits and costs: While the agent is efficient, nontrivial compute is required for pass@k and hierarchical search; budgets must be managed.
- Library coverage: Many targets hinge on Mathlib (and domain-specific libraries) being sufficiently rich; gaps increase proof burden.
- NL-to-formal fidelity: The sketch model presupposes reasonably correct natural-language proofs; errors upstream propagate to formalization.
- Toolchain pinning and reproducibility: Results assume version-pinned Lean/Mathlib; upgrades may break proofs or search behavior.
- Human oversight: Especially in safety-critical or legal contexts, expert review remains necessary to validate semantics, specs, and modeling choices.
Glossary
- Agentic prover: A theorem-proving model that acts as an autonomous agent, invoking tools and constructing proofs via lemmas across multi-turn interactions. "we trained an agentic prover to learn optimal interaction strategies and tool usage for formal theorem proving."
- Agentic reinforcement learning: Reinforcement learning tailored to agents that interact with environments and tools to learn proving strategies at scale. "Seed-Prover 1.5, a formal theorem-proving model trained via large-scale agentic reinforcement learning"
- Backtracking: An inference control technique that restarts from earlier points to explore alternate proof paths when progress stalls. "such as pruning irrelevant intermediate steps or backtracking to restart the conversation at specific points."
- Embedding-based retrieval: Retrieving relevant items (e.g., theorems) by comparing vector embeddings to capture semantic similarity. "For Mathlib search, we use embedding-based retrieval to identify relevant theorems by semantic similarity"
- FATE-H: A benchmark of graduate-level or honors exam difficulty used to evaluate formal proving systems. "FATE-H contains 100 problems at the level of honors course exams or graduate-level difficulty."
- FATE-X: A benchmark of PhD qualifying exam-level difficulty used to evaluate formal proving systems. "FATE-X contains 100 problems at the level of PhD qualifying exams or beyond."
- Formal verification: Mechanized checking of proofs to ensure correctness and eliminate errors. "Consequently, formal verification is widely regarded as a potential paradigm shift for mathematical research."
- Incremental caching mechanism: Storing successfully compiled lemmas to reuse them later, reducing context overhead and regeneration. "This incremental caching mechanism enables more efficient utilization of the context window compared to approaches based on whole-proof generation."
- Interaction budget: Resource limits on the number of turns or sequence length during an inference session. "or when the interaction budget (maximum number of turns or maximum sequence length) is exhausted."
- Lean: An interactive theorem prover and formal proof language used for verifiable mathematical reasoning. "Leveraging Lean\citep{lean4} for mathematical theorem proving offers fully trustworthy verification"
- Lean compiler: The Lean component that compiles and verifies proof code for correctness. "a valid proof is completed and verified by the Lean compiler"
- Lean junk value analysis: Evaluation to detect meaningless or low-value Lean code within generated sketches. "considering factors including alignment with the NL proof, decomposition granularity, difficulty reduction, and Lean junk value analysis."
- Lean sketch (lemma-style): A structured Lean proof outline that decomposes a theorem into auxiliary lemmas (often initially admitted), guiding formalization. "This model synthesizes a lemma-style Lean sketch"
- Light inference: A constrained inference mode that uses self-summarization to retry proving under limited compute. "We can also apply light inference introduced in Seed-Prover \citep{chen2025seed} by applying self-summarizing when the interaction budget is exhausted."
- LLM-as-a-Judge Rubric: An LLM-driven rubric used as a semantic value model to score sketch quality. "an LLM-as-a-Judge Rubric acts as a semantic value model"
- Long Chain-of-Thought (Long-CoT): Extended reasoning sequences used by judge/evaluator models to generalize beyond scalar scoring. "employing Long Chain-of-Thought (Long-CoT) to achieve better generalization than scalar-based models."
- LooKeng: A REPL-based Python interface that compiles Lean proofs and returns structured feedback to the model. "we employ LooKeng~\cite{chen2025seed}, a REPL\textsuperscript{4}-based Python interface that compiles Lean proofs and returns structured feedback to the model."
- Mathlib: The standard mathematics library for Lean containing formalized theorems and definitions. "For Mathlib search, we use embedding-based retrieval"
- Mathlib commit: A specific pinned version of Mathlib used to ensure consistent and reproducible experiments. "calibrated to a fixed Mathlib commit (i.e., v$4.22.0$) to ensure consistency and reproducibility."
- Mathlib search: A tool/process that retrieves relevant Mathlib declarations matched to a query’s semantics. "the model may invoke ``Mathlib search'' to explore available theorems"
- native_decide: An unsafe Lean mechanism for decision procedures that can compromise soundness if misused. "not using any `native_decide' in Putnam, which is unsafe under Lean."
- Natural Language Prover: A component that produces rigorous proofs in natural language to guide formalization. "Natural Language Prover: An LLM optimized for natural language proving (initialized from Doubao-Seed-1.6)."
- Pass@k: A metric/compute budget indicating the number of independent proof attempts or samples (often in multi-pass inference). "This process is viewed as Pass@1 in our setting."
- Pruning: Removing irrelevant steps or branches during inference to streamline the proof search. "such as pruning irrelevant intermediate steps"
- REPL: Read–Eval–Print Loop; an interactive interface for executing and evaluating code step-by-step. "a REPL\textsuperscript{4}-based Python interface that compiles Lean proofs and returns structured feedback to the model."
- ReTool: A framework/approach for reinforcement learning that integrates tool interactions into training. "and follow similar approach in ReTool~\cite{feng2025retool} to enable tool-integrated reinforcement learning."
- Rubric RL: Reinforcement learning guided by an LLM rubric that provides structured, often binary, rewards for outputs. "We trained a sketch model using Rubric RL to bridge natural language proofs with formalization."
- Self-summarization: Generating a summary of a failed trajectory to condition subsequent attempts and improve efficiency. "it performs self-summarization over this trajectory and initiates a new trajectory conditioned on the summary."
- Sketch model: A model that converts natural language proofs into lemma-based Lean sketches to decompose problems. "We train a sketch model to generate lemma-based Lean sketches"
- Step-level interaction: A prover paradigm that issues one tactic per interaction and compiles incrementally at each step. "step-level interaction\citep{wu2024internlm25stepproveradvancingautomatedtheorem,xin2025bfsproverscalablebestfirsttree,xin2025scaling,alphaproof,Aristotle} and whole-proof generation"
- Test-time scaling (TTS): Increasing inference-time compute and search (depth/width) to improve solve rates. "alongside an efficient test-time scaling (TTS) workflow."
- Tool-integrated reinforcement learning: RL where tool calls and responses are interleaved within rollouts to guide learning. "follow similar approach in ReTool~\cite{feng2025retool} to enable tool-integrated reinforcement learning."
- Tool-use agent: The proving agent configured to call tools (Lean, search, Python) under specified limits. "we configure our tool-use agent with a maximum sequence length of 64K and a limit of 28 tool calls."
- VAPO: The RL algorithmic framework used to optimize both the agentic prover and the sketch model. "We implement our RL algorithm based on VAPO~\cite{vapo}"
- Whole-proof generation: A paradigm where the model attempts to produce the entire proof code in a single pass. "approaches based on whole-proof generation."
- Whole-proof mode: Long thinking followed by a single Lean interaction to submit the entire proof. "the whole-proof mode (long thinking followed by a single interaction)"
Collections
Sign up for free to add this paper to one or more collections.