- The paper demonstrates that current UQ methods excel in zero-aleatoric settings but collapse when ambiguity introduces multiple plausible answers.
- It introduces two novel QA datasets, MAQA* and AmbigQA*, to evaluate UQ estimators under realistic, ambiguous conditions using factual co-occurrence statistics.
- The findings suggest that both post-hoc UQ approaches and internal representation probes are unreliable in ambiguous scenarios, highlighting the need for uncertainty-aware training.
Uncertainty Quantification in LLMs: Failure Modes Under Ambiguity
Introduction and Motivation
The paper "The Illusion of Certainty: Uncertainty quantification for LLMs fails under ambiguity" (2511.04418) rigorously investigates the reliability of uncertainty quantification (UQ) methods in LLMs when faced with ambiguous question-answering (QA) tasks. The central thesis is that while current UQ estimators—predictive variation, internal representation probes, and ensemble-based methods—perform adequately in settings with zero aleatoric uncertainty, their efficacy collapses in the presence of ambiguity, i.e., when multiple plausible answers exist for a given question. This is a critical issue for deploying LLMs in real-world, high-stakes domains where ambiguity is inherent.
Theoretical Foundations: Aleatoric vs. Epistemic Uncertainty
The paper formalizes total uncertainty (TU) in LLM predictions as the cross-entropy between the true answer distribution p∗ and the model's predicted distribution p. This decomposes into aleatoric uncertainty (AU), the entropy of p∗, and epistemic uncertainty (EU), the KL-divergence KL(p∗∥p). AU is irreducible and reflects intrinsic data ambiguity, while EU is reducible and reflects model ignorance.
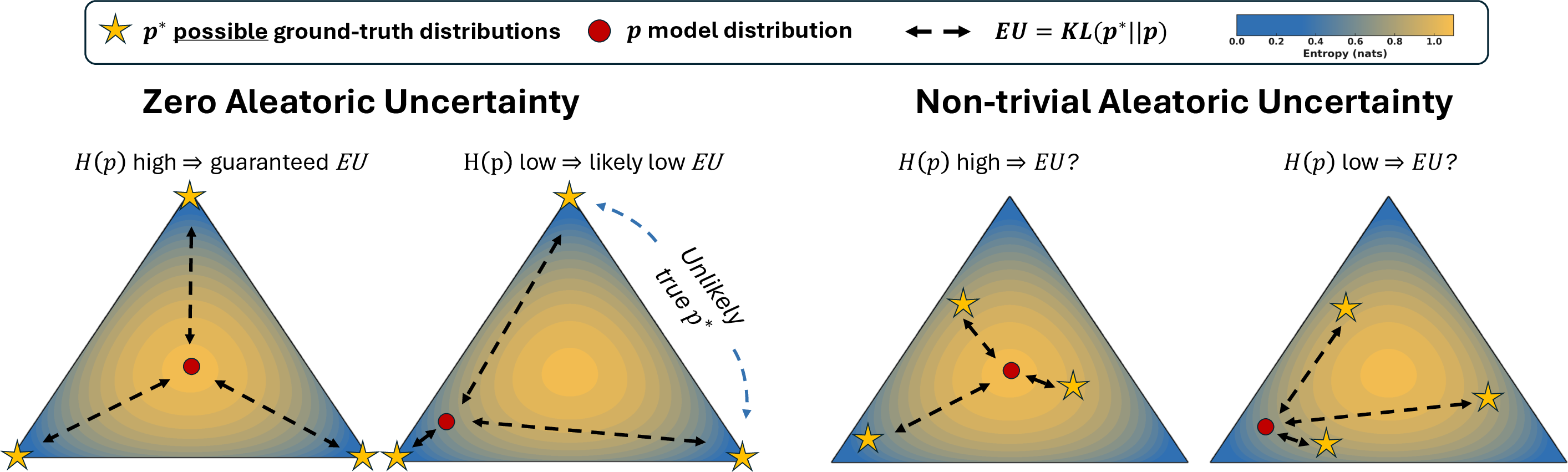
Figure 1: Theoretical insights on the 3-class simplex; under zero AU, high entropy in p guarantees high EU, but under non-trivial AU, entropy in p is uninformative about EU.
The theoretical analysis demonstrates that in the zero-AU regime, EU reduces to the negative log-likelihood of the correct answer, and predictive entropy or mutual information (MI) from ensembles are reliable proxies for EU. However, when AU is non-zero, the location of p∗ in the probability simplex is unconstrained, and no function of p alone can reliably distinguish epistemic from aleatoric uncertainty.
Benchmarking Under Ambiguity: MAQA* and AmbigQA*
To enable principled evaluation of UQ under ambiguity, the authors introduce MAQA* and AmbigQA*, two QA datasets with explicit ground-truth answer distributions p∗, estimated via factual co-occurrence statistics in large corpora (primarily English Wikipedia). This frequentist approach is justified by empirical correlations between co-occurrence and LLM output probabilities, and by theoretical arguments that, in the infinite data limit, model predictions should converge to the pretraining distribution.
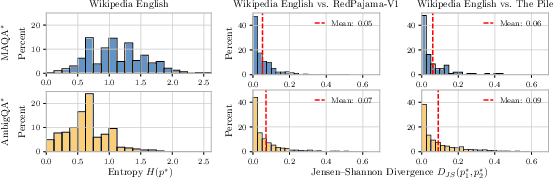
Figure 2: Left: Distribution of ground-truth entropy H(p∗) across MAQA
and AmbigQA*; Right: JS divergence between different proxies for estimating
p∗, indicating high alignment.*
The datasets span a wide range of AU, enabling systematic paper of UQ estimators in both unambiguous and ambiguous regimes.
Empirical Results: Collapse of UQ Estimators Under Ambiguity
The paper evaluates three families of UQ estimators:
- Predictive Variation: Semantic Entropy (SE), Maximum Sentence Probability (MSP), Shifting Attention to Relevance (SAR), and Iterative Prompting (IP).
- Internal Representations: Linear and MLP probes on residual stream activations.
- Ensembles: MI computed over predictions from LLaMA3.1 8B, Gemma3 12B, and Qwen2.5 14B.
In the zero-AU setting (e.g., TriviaQA), all estimators achieve high concordance (AUCc) scores, reliably ranking samples by EU. However, in MAQA* and AmbigQA*, AUCc scores for all estimators degrade to near-random (0.5–0.6), indicating a failure to distinguish high and low EU.

Figure 3: Relationship between prediction-based estimators and true EU for Gemma 3-12B on MAQA
; correlation vanishes under non-trivial AU, and ROC curves approach random performance.*
Theoretical results (Proposition: Non-Identifiability of EU) prove that for any function f(p), there exist p1∗ and p2∗ such that EU is either zero or large, making f(p) uninformative about EU under ambiguity. Similarly, MI from ensembles is shown to be unreliable: high MI does not imply high EU when AU is non-trivial.
Internal Representation Probes: No Reliable Signal Under Ambiguity
Empirical analysis of linear and MLP probes on model activations reveals that, while deeper layers encode EU in the zero-AU regime, probe performance collapses under ambiguity. This suggests that model internals do not retain additional signal for EU beyond what is present in the predictive distribution.
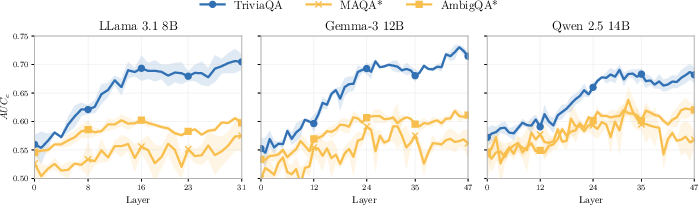
Figure 4: MLP regression performance across layers; probe ranking capability collapses under non-trivial AU.
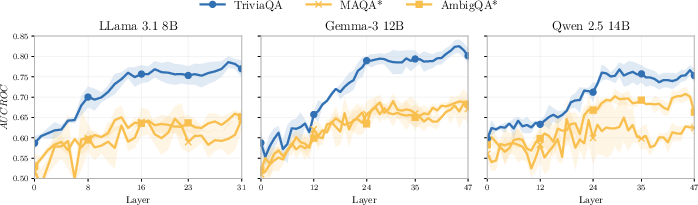
Figure 5: MLP classification performance across layers; separation capability collapses under non-trivial AU.
Robustness and Ablations
The findings are robust across different p∗ estimation strategies (Wikipedia, RedPajama-V1, The Pile), model sizes, and perturbations of p∗ via Dirichlet priors. Notably, instruct models exhibit entropy collapse, outputting near-deterministic answers even when AU is high, further degrading UQ estimator performance.
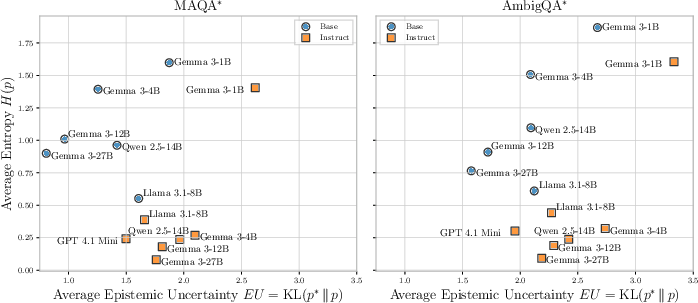
Figure 6: Entropy collapse of Instruct models on MAQA
and AmbigQA*.*
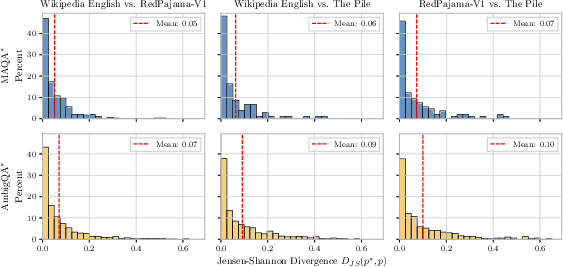
Figure 7: Comparison of retrieved ground-truth distribution p∗ using different strategies; low JS divergence validates consistency.
Implications and Future Directions
The paper's results have significant implications:
- Current UQ paradigms are fundamentally unreliable under ambiguity. This is both empirically and theoretically substantiated.
- Post-hoc UQ methods are insufficient. Reliable EU estimation in the presence of AU requires models to be explicitly trained to encode uncertainty, potentially via higher-order or evidential approaches.
- Benchmarking must account for ambiguity. The release of MAQA* and AmbigQA* enables rigorous evaluation of future UQ methods in realistic settings.
The authors suggest that future work should focus on training LLMs to model joint distributions over answers, or to learn second-order uncertainty representations, as in evidential deep learning or higher-order calibration frameworks.
Conclusion
This paper provides a comprehensive theoretical and empirical analysis of the failure modes of uncertainty quantification in LLMs under ambiguity. The introduction of new benchmarks and the demonstration of estimator collapse highlight a critical gap in current methodologies. The work motivates a paradigm shift toward uncertainty-aware training and evaluation, with direct implications for the safe and trustworthy deployment of LLMs in ambiguous, real-world tasks.








