- The paper introduces a two-phase decoding framework called Latent Refinement Decoding (LRD) that refines belief states in the embedding space before token commitment.
- The methodology employs soft diffusion with entropy-based mixing and a KL divergence threshold to adaptively finalize tokens, improving information propagation.
- Empirical results show up to +6.3 points improvement in pass@1 and speedups of up to 10.6×, demonstrating robust gains in accuracy and efficiency.
Latent Refinement Decoding for Diffusion-Based LLMs
Introduction and Motivation
Diffusion-based LLMs (dLLMs) have emerged as a promising alternative to autoregressive (AR) models for natural language generation, offering parallel decoding and significant inference speedups. However, standard diffusion decoding strategies are hampered by two principal limitations: (1) information loss due to hard masking, where predictive distributions for uncertain positions are discarded at each step, and (2) inefficient convergence dynamics, as hard assignment either commits prematurely or slows progress by excessive remasking. The paper introduces Latent Refinement Decoding (LRD), a two-stage decoding framework designed to address these issues by refining belief states in the embedding space before discrete token commitment.
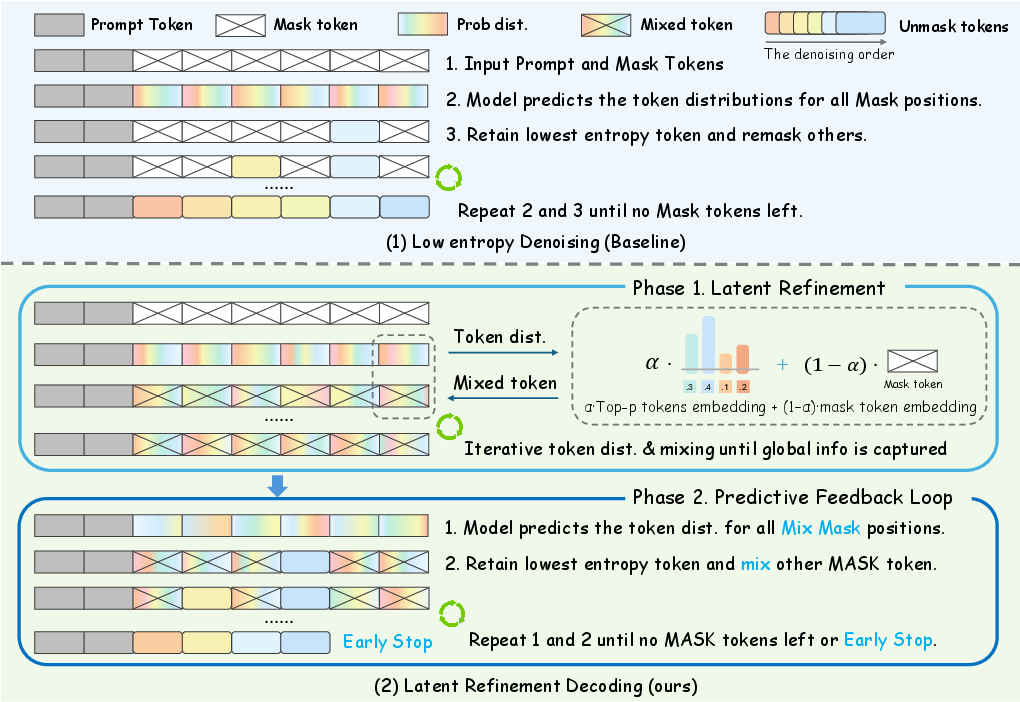
Figure 1: Comparison between the existing decoding strategy and the proposed method. In LRD, Phase 1 refines each [MASK] embedding, and Phase 2 progressively commits confident tokens while keeping uncertain ones soft for context-aware decoding.
Methodology
Soft Diffusion in Embedding Space
LRD departs from the binary decision paradigm of hard masking by introducing a soft diffusion phase. Instead of resetting uncertain positions to a uniform [MASK] embedding, LRD forms mixed embeddings for each masked position. These are constructed as convex combinations of the [MASK] embedding and the entropy-normalized expectation over the top-p predicted token embeddings. The mixing coefficient αt(i) is entropy-dependent, ensuring that high-entropy (uncertain) positions remain mask-like, while low-entropy (confident) positions incorporate more token-specific information. This continuous relaxation allows the model to propagate uncertainty and partial beliefs across positions via self-attention, facilitating globally coherent belief formation before discrete decisions.
Adaptive Two-Phase Decoding
LRD employs a two-phase decoding schedule:
- Phase 1: Latent Refinement
The model iteratively updates soft embeddings for all positions, refining predictive distributions in the embedding space. Convergence is monitored by the average KL divergence between consecutive predictive distributions. When the KL divergence falls below a threshold, indicating stabilization of beliefs, the process transitions to Phase 2.
- Phase 2: Predictive Feedback Loop
Confident positions (low entropy) are finalized as discrete tokens, while uncertain positions retain their soft embeddings. This hybrid representation is iteratively updated, with the predictive feedback loop allowing uncommitted positions to benefit from the context provided by finalized tokens. Early stopping is governed by a KL-based criterion, enabling adaptive termination of decoding based on actual convergence rather than a fixed number of steps.
This design ensures that information is preserved throughout the generation process, and that the model can adaptively allocate computation based on the complexity of the generation task.
Empirical Results
Accuracy and Efficiency
LRD demonstrates consistent improvements in both accuracy and inference speed across a range of benchmarks, including code generation (HumanEval, MBPP) and mathematical reasoning (GSM8K, MATH500). For example, on HumanEval, LRD achieves up to +6.3 points improvement in pass@1 over the Dream-Base-7B baseline at 256 tokens. Similar gains are observed across other tasks and sequence lengths. Notably, LRD delivers speedups of up to 10.6× for long sequences, with the largest gains realized in large-context scenarios.
Convergence Dynamics
KL divergence analysis reveals that the latent refinement phase rapidly drives the model's predictive distributions toward a stable fixed point, after which the predictive feedback loop efficiently sharpens confidence and finalizes tokens.
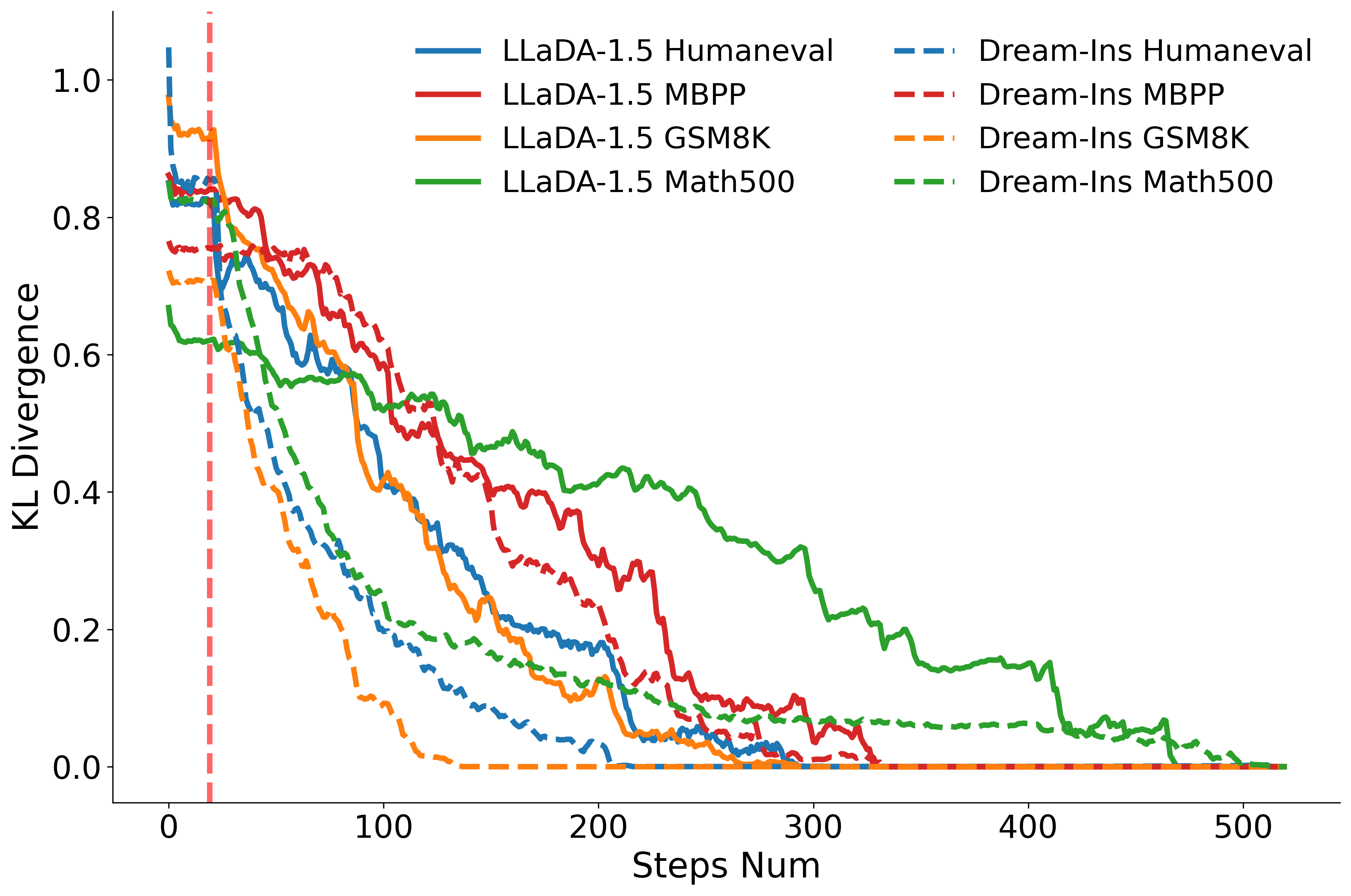

Figure 2: KL divergence between step-wise predictive distributions and final decoded results for LLaDA-1.5 and Dream-Ins across benchmarks. The red vertical line marks where decoding begins after a fixed 20-step latent refinement.
Most examples converge within the first few latent refinement steps, confirming the efficiency of the soft diffusion phase and justifying the use of adaptive early stopping.
Ablation Studies
Ablation experiments highlight the critical role of both latent refinement and mixed embeddings. Removing either component degrades accuracy, with the absence of mixed embeddings causing the largest drop. Early stopping is identified as the primary driver of speedup, with negligible impact on accuracy. Excessive latent refinement beyond the initial phase yields diminishing returns and slows decoding.
Sensitivity to Mixing Parameters
The maximum mixing ratio rf and the top-p nucleus set size are key hyperparameters. The results indicate that intermediate values of rf yield the best trade-off between stability and information propagation; both extremes (no mixing or full mixing) are suboptimal.
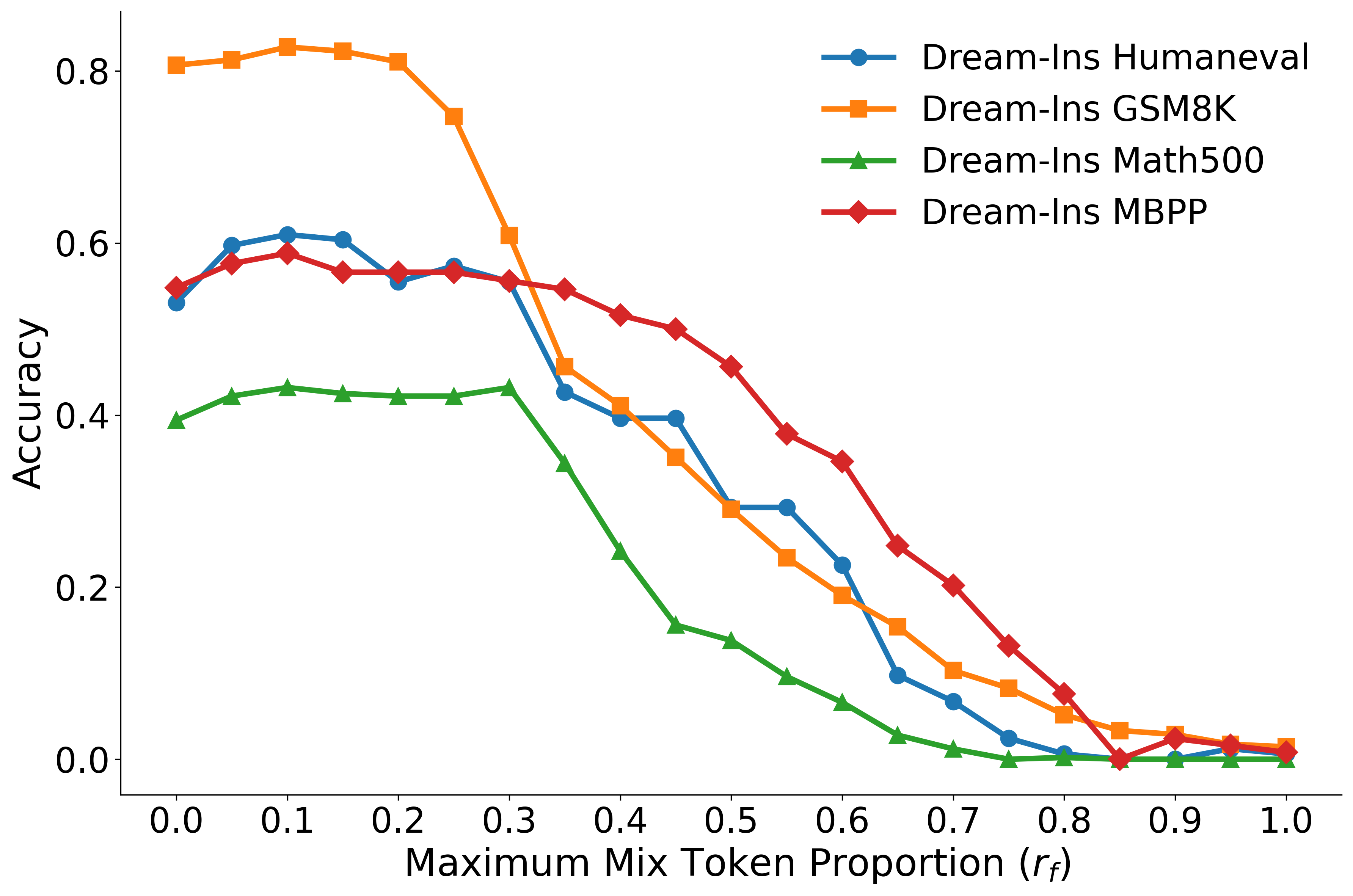
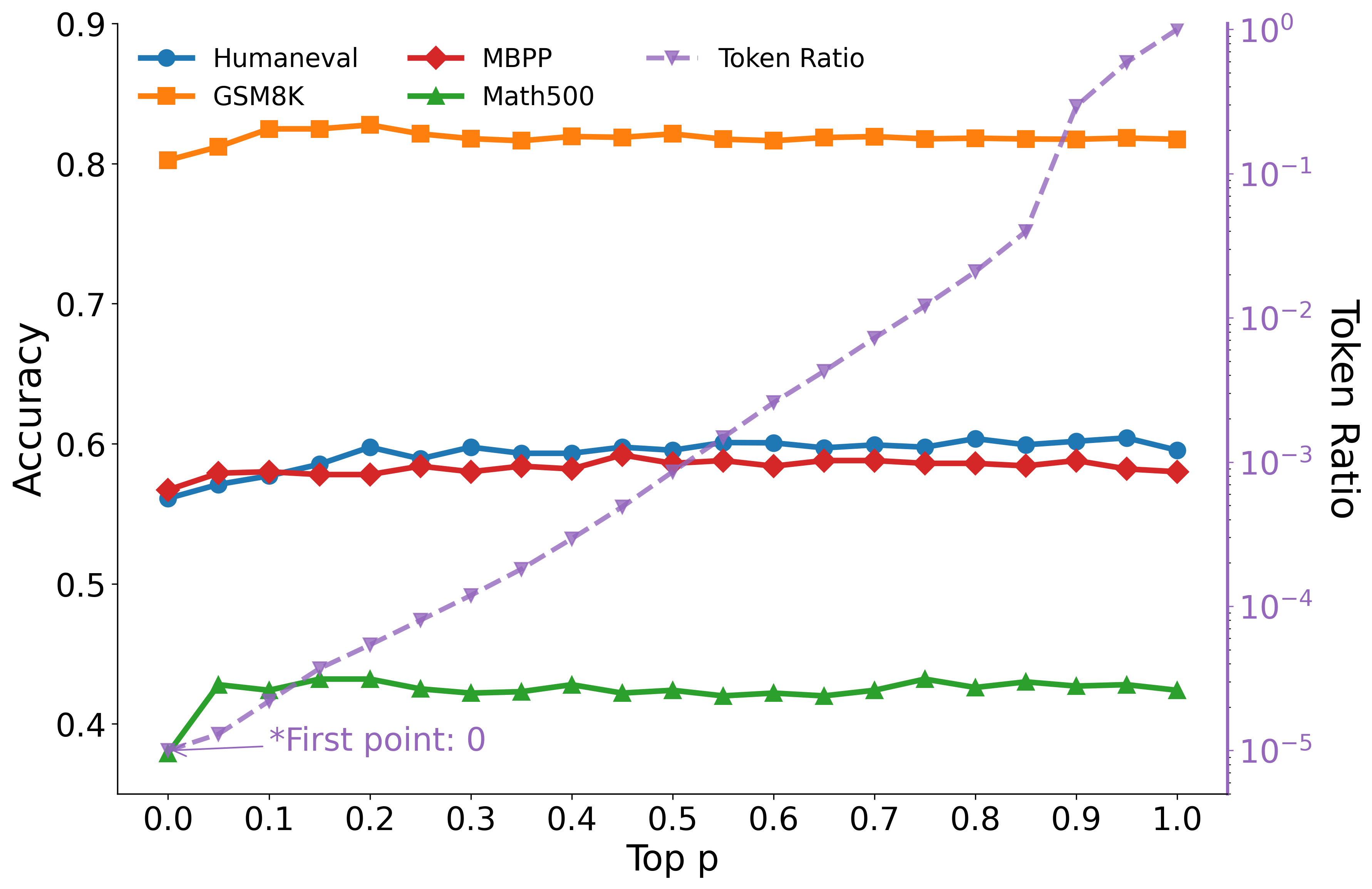
Figure 3: Accuracy of Dream-Ins on four benchmarks under different Maximum token proportion, where rf=0 corresponds to no mixing.
Increasing the top-p value for mixing quickly improves performance, but further increases beyond p≈0.2 offer little additional benefit, indicating that the presence of mixing is more important than the absolute number of tokens included.
Theoretical and Practical Implications
LRD provides a principled approach to mitigating information loss in diffusion decoding by leveraging continuous relaxation in the embedding space. The use of entropy-based mixing and KL-driven early stopping aligns the decoding process with the underlying uncertainty in the model's predictions, supporting both efficient exploration and rapid convergence. The framework is model-agnostic and can be integrated into existing dLLMs without architectural modifications.
From a theoretical perspective, the local Lipschitz analysis of the mixed embedding updates suggests practical stability, even though global convergence guarantees remain intractable due to the complexity of transformer dynamics. Empirical evidence supports the claim that the method is robust across a range of settings and model families.
Future Directions
LRD opens several avenues for further research and practical deployment:
- Integration with Systems-Level Optimizations: Combining LRD with KV caching, speculative decoding, and hardware-aware acceleration could further enhance inference efficiency.
- Extension to Multimodal and Structured Generation: The soft-to-hard refinement paradigm may generalize to other domains where uncertainty propagation and adaptive commitment are beneficial.
- Theoretical Analysis: Deeper analysis of the convergence properties of mixed embedding updates in high-capacity transformers could yield stronger guarantees and inform hyperparameter selection.
Conclusion
Latent Refinement Decoding addresses fundamental limitations of diffusion-based LLM decoding by introducing a two-stage process that preserves and refines belief states before discrete token commitment. The approach yields consistent improvements in both accuracy and efficiency, particularly for long sequences and complex tasks. LRD is a flexible, theoretically motivated, and empirically validated framework that advances the state of the art in parallel sequence generation with diffusion models. Its modularity and compatibility with existing architectures position it as a strong candidate for future research and deployment in high-throughput language generation systems.






