Why Can't Transformers Learn Multiplication? Reverse-Engineering Reveals Long-Range Dependency Pitfalls (2510.00184v1)

Abstract: LLMs are increasingly capable, yet still fail at a seemingly simple task of multi-digit multiplication. In this work, we study why, by reverse-engineering a model that successfully learns multiplication via \emph{implicit chain-of-thought}, and report three findings: (1) Evidence of long-range structure: Logit attributions and linear probes indicate that the model encodes the necessary long-range dependencies for multi-digit multiplication. (2) Mechanism: the model encodes long-range dependencies using attention to construct a directed acyclic graph to cache'' andretrieve'' pairwise partial products. (3) Geometry: the model implements partial products in attention heads by forming Minkowski sums between pairs of digits, and digits are represented using a Fourier basis, both of which are intuitive and efficient representations that the standard fine-tuning model lacks. With these insights, we revisit the learning dynamics of standard fine-tuning and find that the model converges to a local optimum that lacks the required long-range dependencies. We further validate this understanding by introducing an auxiliary loss that predicts the ``running sum'' via a linear regression probe, which provides an inductive bias that enables the model to successfully learn multi-digit multiplication. In summary, by reverse-engineering the mechanisms of an implicit chain-of-thought model we uncover a pitfall for learning long-range dependencies in Transformers and provide an example of how the correct inductive bias can address this issue.

• The paper demonstrates that ICoT training enables transformers to capture long-range dependencies essential for multi-digit multiplication, unlike standard fine-tuning.
• The analysis reveals that intermediate representations, such as the computed value ˆcₖ and attention tree structures, are critical for predicting carries and partial products accurately.
• The study proposes an auxiliary loss technique to mitigate long-range learning deficits, fostering a structural inductive bias in Transformer architectures.

Why Can't Transformers Learn Multiplication? Reverse-Engineering Reveals Long-Range Dependency Pitfalls

Introduction

The paper explores why Transformers struggle with multi-digit multiplication, a relatively simple algorithmic task. Despite the prowess of LLMs such as LLaMA-3.2 and GPT-4, they fail at 4x4-digit multiplication. This investigation involves examining the inner workings of a model trained using Implicit Chain-of-Thought (ICoT), uncovering its successful handling of long-range dependencies, in contrast to standard fine-tuning methods which falter.

Long-Range Dependencies in Multiplication

Multi-digit multiplication inherently involves computing pairwise products of digits and accounting for carries over extended positions. The paper outlines a key intermediary term, $\hat{c}_k = s_k + r_{k-1}$, crucial for encapsulating these dependencies. While ICoT models align with these dependencies through explicit chain-of-thought training, standard fine-tuning lacks this structural insight, often leading to local optima and unsuccessful learning.

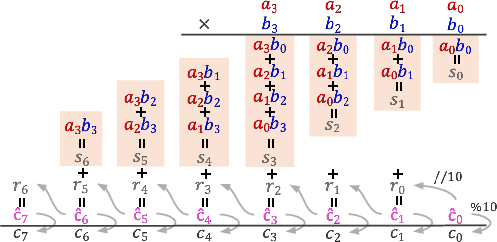
Figure 1: Multiplication has long-range dependencies, which can be captured by an intermediate value $\hat{c}_i$, from which both the solution ($c_i$) and carries ($r_i$) can be derived.

Evidence of Long-Range Dependencies

Logit Attributions

Logit attribution analysis reveals that, unlike standard fine-tuned models, ICoT models discern each digit's influence on the eventual product, demonstrating successful learning of the requisite dependencies.

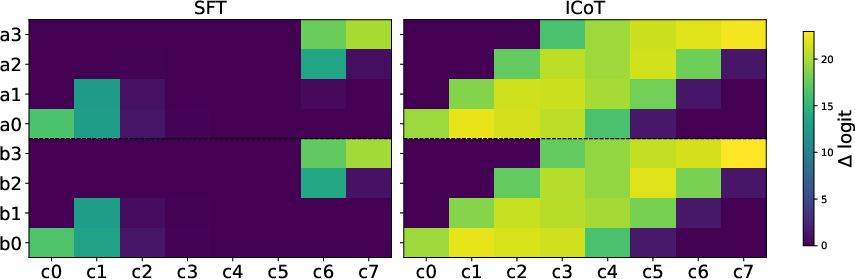
Figure 2: Logit Attribution. We test for whether each model has correctly learned long-range dependencies by measuring how sensitive the logits of output digits $c_i$ are to each operand digit (i.e., $a_i, b_j$).

Probing for Intermediary Terms

Linear probes establish that ICoT models encode intermediate values like $\hat{c}_k$ effectively, whereas fine-tuned models fail to develop such comprehensive representations.

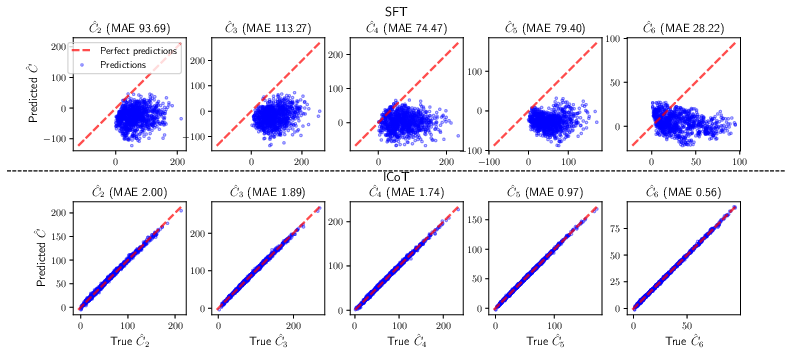
Figure 3: Linear regression probing results for $\hat{c_k}$. We probe from the middle of the last Transformer block, after attention heads but before MLPs.

Mechanisms for Encoded Dependencies

Attention Trees

ICoT models create a directed acyclic graph structure, akin to binary trees, using attention heads to track necessary pairwise products and store these calculations for later retrieval when predicting solutions.

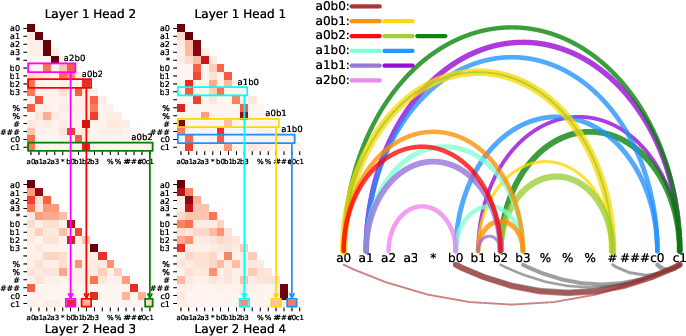
Figure 4: Visualization of attention tree to compute $c_2$. Attention maps show cache and retrieval patterns.

Geometric Representations of Features

1. Minkowski Sums: Attention heads realize partial products as Minkowski sums, providing an efficient combination of attended inputs (Figure 5).
2. Fourier-based Digit Embeddings: Digits are embedded using Fourier bases, forming visually identifiable structures that represent even and odd number sequences efficiently (Figure 6).

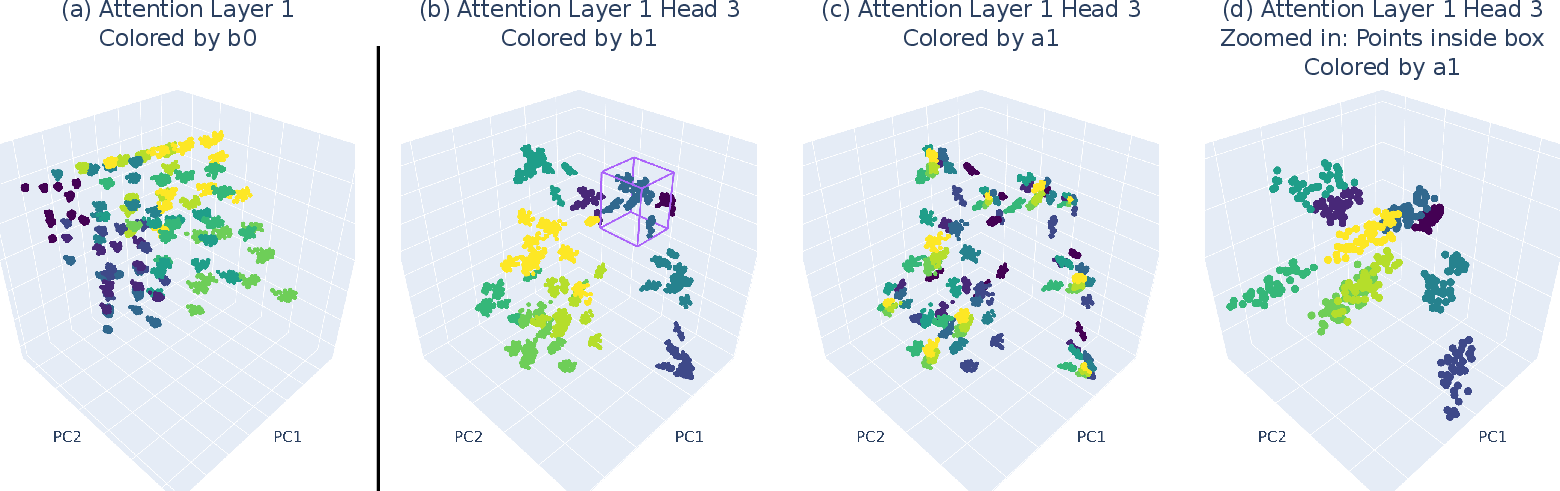
   Figure 5: 3D PCA of attention head outputs can form Minkowski sums, which in turn can form nested representations.

   

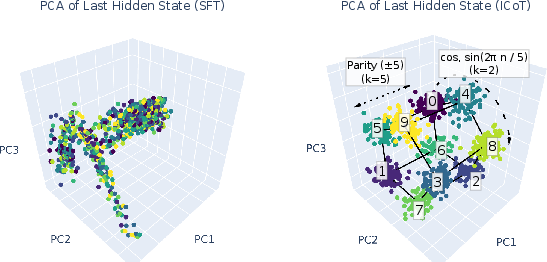
   Figure 6: Digits embedded in a pentagonal prism, using Fourier bases.

Learning Limitations of Transformers

Analysis of training dynamics shows standard fine-tuning often results in learned solutions for only the first, second, and last digits. Middle digits remain elusive due to insufficient long-range information propagation.

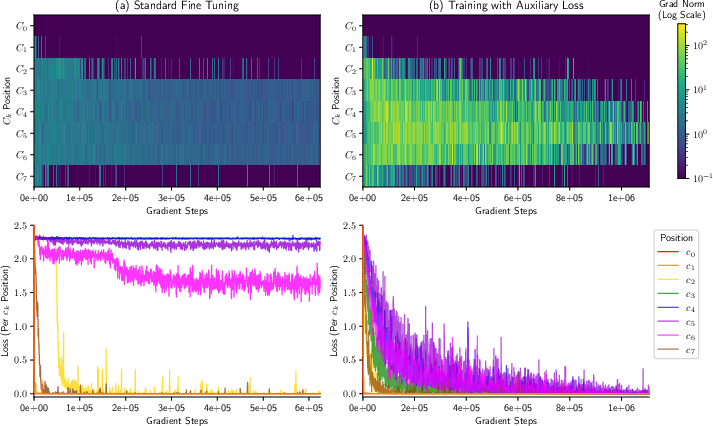
Figure 7: Gradient norms and losses per token $c_k$. Loss plateau and erratic gradients illustrate the pitfalls of insufficient long-range dependency learning.

Inductive Bias for Effective Multiplication Learning

The paper introduces an auxiliary loss to guide Transformers towards better dependency handling, allowing prediction of intermediate sums without explicit chain-of-thought guidance. This strategy shows promise in overcoming existing shortcomings within Transformer architectures.

Conclusion

The paper reveals the crucial role of long-range dependencies in learning multi-digit multiplication and highlights structural deficits in standard fine-tuning approaches. While ICoT provides task-specific improvements, future AI advancements must focus on more general solutions for handling long-range dependencies effectively in complex tasks.