Linear Probes: Neural Network Diagnostics
- Linear probes are simple, independently trained linear classifiers added to intermediate layers to gauge the linear separability of features.
- They reveal how semantic content evolves across network depths, providing actionable insights for model interpretability and performance assessment.
- By isolating layer-specific diagnostics, linear probes inform strategies for pruning, compression, and deep supervision in various domains.
Linear probes are simple, independently trained classifiers—typically linear models such as softmax regression—attached to intermediate layers of neural networks to assess the linear separability and semantic content of representations at various depths. They serve as non-intrusive diagnostic tools by providing a direct measure of how features at each layer support a specific prediction or classification objective, thereby illuminating the functional dynamics and interpretability of deep models across architectures and domains.
1. Definition and Functional Role
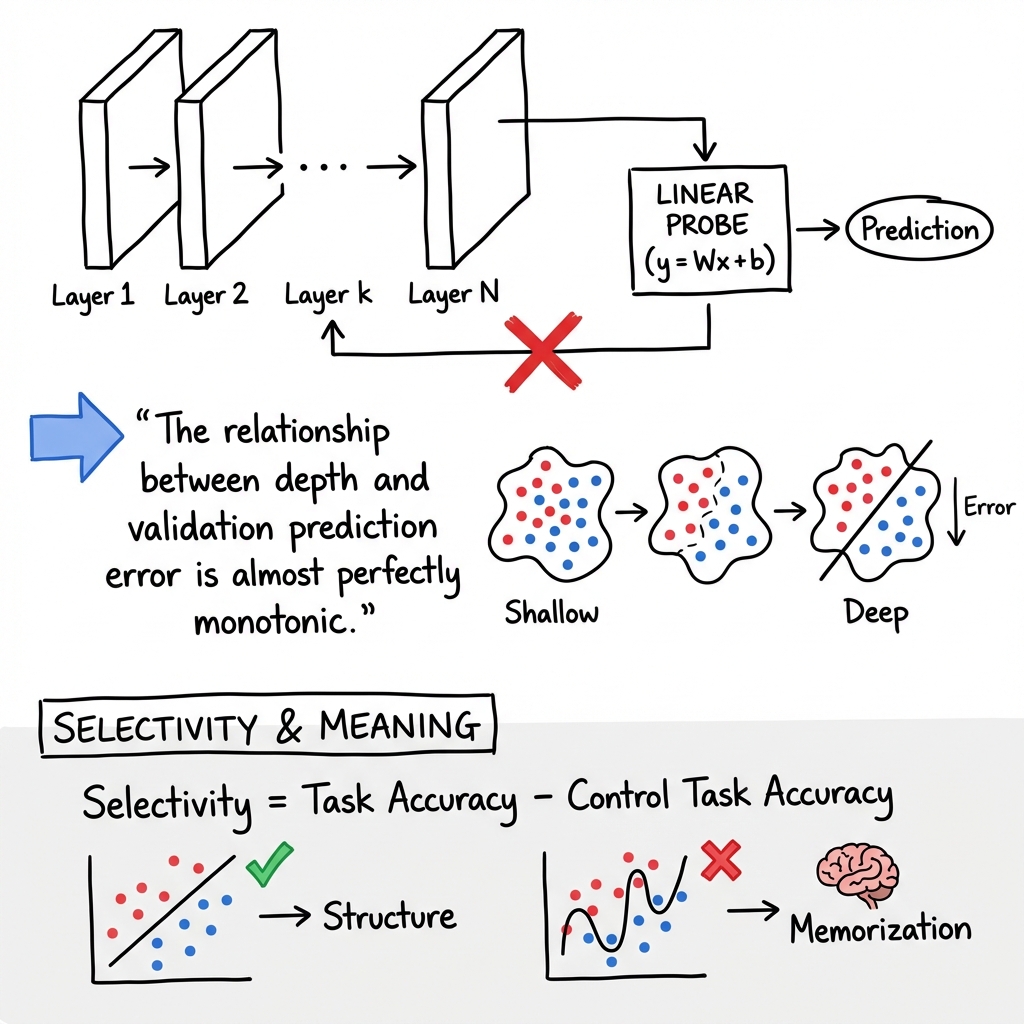
A linear probe is defined as a linear classifier or regressor trained post hoc—without altering the parameters of the main network—on the activations (feature vectors) extracted at a given intermediate layer. Mathematically, for features at layer , a probe is parameterized by weights and bias :
for classification tasks, or
for regression. Probes are optimized using a convex objective (such as cross-entropy loss for classification), with gradients not propagated to the backbone model, enforced by operations like tf.stop_gradient.
Their primary function is to quantify the extent to which the desired information is encoded in a linearly accessible form at each layer. By measuring probe accuracy (or loss), researchers can determine which features are developed, at what depth, and how readily they can be used for downstream tasks.
2. Methodologies and Deployment Practices
Insertion and Training
- For each selected layer in the primary network (e.g., ResNet-50, Inception v3, LLMs), activations are extracted and used as features for a linear probe.
- Probes are trained independently of the model’s own training process, usually on a dataset split to avoid confounding optimization.
- To limit overfitting and maintain tractability, high-dimensional representations may be reduced using random feature subsampling or pooling operations.
Probe Objectives and Techniques
- Task labels need not match the original supervised objectives; probes can target diverse properties such as class labels, syntactic roles, world features, or security vulnerabilities.
- Regularization (such as L2 penalty or rank constraints) and capacity control are important—empirical studies show regularization increases the selectivity of probes, reducing their propensity to memorize superficial cues (1909.03368).
- For probing compositional or relational structure, extensions such as propositional or structural probes have been developed (see Section 6).
Evaluation
- Probe performance is typically reported as classification accuracy, cross-entropy loss, AUC, , or correlation with ground-truth features.
- In model compression or pruning, probe accuracy at each layer informs early estimates of post-compression model performance and guides pruning decisions (2505.24451).
3. Interpretive Insights and Diagnostic Applications
Linear Separability Across Depth
A central empirical finding is that in deep feedforward networks, linear separability of features (as measured by optimal probe performance) increases monotonically with depth. This is observed consistently in canonical architectures such as ResNet-50 and Inception v3:
| Layer | Feature Size | Probe Validation Error |
|---|---|---|
| input_1 | (224, 224, 3) | 0.99 |
| add_1 | (28, 28, 256) | 0.94 |
| ... | ... | ... |
| add_16 | (7, 7, 2048) | 0.31 |
"The relationship between depth and validation prediction error is almost perfectly monotonic." (1610.01644)
This reflects that, while information content may only decrease by the Data Processing Inequality (), later layers create representations that are more convenient for linear classification.
Model Diagnostics
Linear probes enable quantitative localization of where learning and information flow occurs within a model:
- Identification of "dead" or ineffective segments, as evidenced by flat or anomalously high probe error profiles.
- Understanding the utility of skip connections or auxiliary branches by comparing probe accuracy across different segments.
- Tracking probe performance epochs provides insight into how representations evolve during training.
Confidence Scoring and Uncertainty Estimation
Probes deployed at multiple layers can be used as features to a meta-model for confidence estimation. For instance, in whitebox meta-models, the concatenated outputs of all probes are input to a secondary classifier (logistic regression or gradient boosting) to predict model confidence, outperforming blackbox approaches under noise and out-of-domain shifts (1805.05396).
4. Implications for Representation Learning, Interpretability, and Model Compression
Probing as an Interpretability Tool
By providing a direct readout of which properties are present in representations, linear probes serve as a principled basis for network interpretation. In NLP, linear probes reveal which layers in contextualized encoders (such as ELMo and BERT) encode syntactic, lexical, or positional information, and expose disentangled subspaces when regularization (e.g., orthogonal constraints) is enforced (2012.15228).
Guidance of Compression Strategies
LP-based approaches such as LPASS leverage per-layer probe accuracy on side tasks (e.g., cyclomatic complexity in code) to select compression cutoffs that do not compromise downstream accuracy (2505.24451). This diagnostic use offers substantial computational savings by enabling fast, interpretable pruning and early performance estimation.
Deep Supervision and World Modeling
Adding a probe-based loss (deep supervision) during training can encourage intermediate network states to encode world features in more linearly decodable forms. As demonstrated in world modeling for partial observation tasks, this supervision improves both representation quality and resource efficiency, with a supervised model achieving similar performance as a model twice its size (2504.03861).
5. Limitations, Selectivity, and Best Practices
Selectivity and Memorization
Probes with too high capacity (deep MLPs, large hidden layers) can memorize or exploit superficial cues, such as word identity rather than true encoded structure (1909.03368). The notion of selectivity—defined as the gap between linguistic and control task accuracy—
—is central for meaningful interpretation. High selectivity from a linear probe indicates features are truly encoded in representation, rather than artifacts of the probe.
Limitations
- In clean data settings, probe-based confidence models may not outperform simple softmax response baselines; their main advantages are robustness to noise and distribution shift.
- Probe outcomes may be correlational, not causal: directions found by probing may not be actively used by the model’s output head (2503.17755).
- Linear probes reveal only linearly accessible structure; non-linear phenomena remain invisible unless more expressive probes are used, though these introduce interpretability trade-offs.
6. Extensions: Structural and Propositional Probes
Structural probes decompose the linear map into rotation and scaling components to match, for example, the topology of linguistic parse trees in NLP (2012.15228). Enforcing orthogonality restricts overfitting and enables the identification of distinct subspaces for syntactic vs. lexical features, increasing interpretability.
Propositional probes extend linear probes by composing per-token attributes into logical predicates using a learned binding subspace, uncovering compositional world knowledge that persists even when the model output is manipulated by prompt injection or backdoors (2406.19501).
7. Practical Applications Across Domains
Linear probes have been applied to:
- Computer vision: characterization of layer-wise feature generality (1610.01644), assessment of medical imaging representations (2107.11468).
- NLP: quantifying encodings of syntax, semantics, and factual knowledge (1909.03368, 2012.15228).
- Security: guiding efficient compression and pruning of LLMs for code vulnerability detection without performance tradeoff (2505.24451).
- World models: deep supervision for latent decodability and stability in agents trained under partial observation (2504.03861).
- Safety and alignment: detection of deception, robust preference extraction, and monitoring for prompt attacks or backdoors (2502.03407, 2503.17755, 2406.19501).
Summary Table: Core Linear Probe Properties
| Aspect | Description |
|---|---|
| Training | On fixed representations, gradients do not update main model |
| Objective | Predict task labels, world features, or auxiliary traits via linear map |
| Key utility | Diagnosing feature evolution, layer selection for pruning, decodability, robust uncertainty |
| Interpretability | High for low-capacity (linear) probes; tradeoff with expressivity for complex tasks |
| Main caveats | Interpretability of accuracy (selectivity), limitation to linear content, probe memorization |
Linear probes represent a versatile, theoretically grounded, and computationally efficient methodology for both interpreting neural networks' inner workings and guiding practical decisions in network design, compression, supervision, and monitoring. Their correct and selective application requires careful attention to regularization, control tasks, and alignment with the intended interpretive or diagnostic goal.