LeanGeo: Formalizing Competitional Geometry problems in Lean (2508.14644v1)

Abstract: Geometry problems are a crucial testbed for AI reasoning capabilities. Most existing geometry solving systems cannot express problems within a unified framework, thus are difficult to integrate with other mathematical fields. Besides, since most geometric proofs rely on intuitive diagrams, verifying geometry problems is particularly challenging. To address these gaps, we introduce LeanGeo, a unified formal system for formalizing and solving competition-level geometry problems within the Lean 4 theorem prover. LeanGeo features a comprehensive library of high-level geometric theorems with Lean's foundational logic, enabling rigorous proof verification and seamless integration with Mathlib. We also present LeanGeo-Bench, a formal geometry benchmark in LeanGeo, comprising problems from the International Mathematical Olympiad (IMO) and other advanced sources. Our evaluation demonstrates the capabilities and limitations of state-of-the-art LLMs on this benchmark, highlighting the need for further advancements in automated geometric reasoning. We open source the theorem library and the benchmark of LeanGeo at https://github.com/project-numina/LeanGeo/tree/master.

• The paper introduces LeanGeo, a framework that formalizes competition-level geometry problems using Lean 4 for rigorous proof verification.
• It presents LeanGeo-Bench, a formal benchmark sourced from IMO problems, to evaluate advanced large language models and automated theorem provers.
• The framework integrates cross-disciplinary mathematical domains, demonstrating potential to enhance automation and scalability in geometric reasoning.

LeanGeo: Formalizing Competitional Geometry Problems in Lean

The paper "LeanGeo: Formalizing Competitional Geometry Problems in Lean" introduces LeanGeo, a framework for formalizing and solving competition-level geometry problems using the Lean 4 theorem prover. This paper outlines the design, implementation, and applications of LeanGeo, together with its implications for advancing the field of automated geometric reasoning.

Introduction to LeanGeo

LeanGeo is developed to overcome the challenges in formalizing geometry problems that are often encountered in mathematical competitions. It strives for a unified system that not only addresses these issues but also integrates seamlessly with other mathematical domains. One significant aspect of LeanGeo is its extensive library of geometric theorems, built upon Lean's foundational logic, which aids in rigorous proof verification.

LeanGeo's inception is motivated by the limitations of existing geometry solving systems, which are often isolated and unable to integrate with a broader mathematical framework, such as algebra or number theory. The LeanGeo framework provides a comprehensive set of tools for formalizing geometric problems, hence facilitating the inclusion of cross-disciplinary mathematical concepts.

Figure 1: Structure of LeanGeo Theorem Library.

LeanGeo-Bench: A Formal Geometry Benchmark

This work also introduces LeanGeo-Bench, a formal benchmark of geometry problems expressed within LeanGeo. The benchmark consists of problems sourced from the International Mathematical Olympiad (IMO) and other advanced competitions. This makes it a suitable testbed for evaluating the reasoning capabilities of state-of-the-art LLMs and proof systems.

The LeanGeo-Bench covers a wide range of geometric topics and structures, such as triangles, circles, and key geometric points like circumcenters and orthocenters. These provide a rigorous environment for testing new methods in automated theorem proving (ATP).

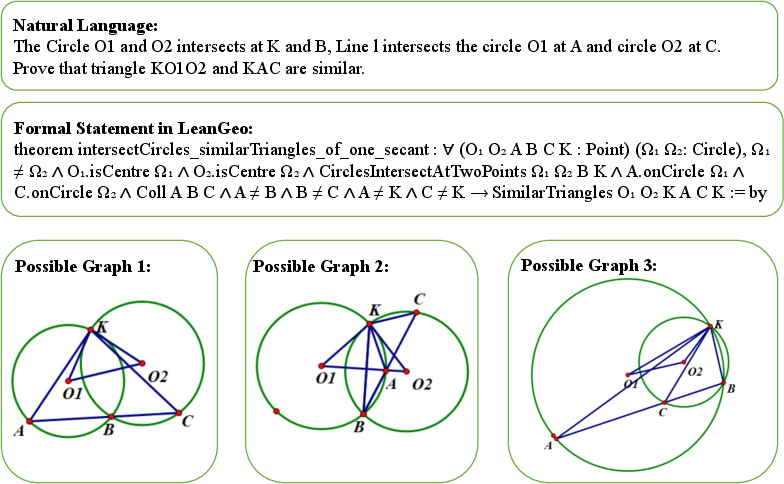
Figure 2: Different graphs with a same formal statement.

Implementation and Applications

LeanGeo is constructed atop the axiomatic framework of SystemE, with enhancements that accommodate a broader scope of geometric reasoning. The integration with LeanSMT allows for efficient proof checking and validation within the Lean environment.

The theorem library of LeanGeo comprises a substantial array of formalized theorems, facilitating the development of proofs in a declarative language that is easily interpretable. This is pivotal for enabling interaction with advanced geometric tools from other mathematical disciplines, thus broadening the applicable scope of theorems beyond the typical geometry systems.

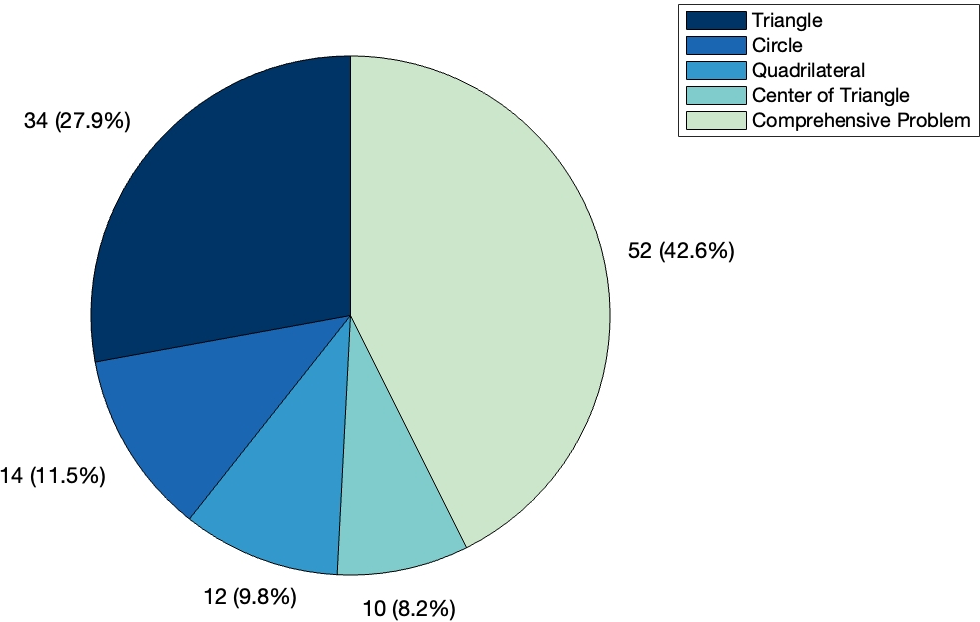
Figure 3: Category Distribution of LeanGeo-Bench.

Results from Initial Experiments

Preliminary experiments conducted with LeanGeo-Bench demonstrated varying levels of performance across different LLMs, underscoring the complexity of geometric reasoning tasks. These results highlight the potential of LeanGeo as a benchmark for gauging the future development of formal mathematics systems and assessing their ability to handle intricate geometric problems.

The trials also suggest that current systems have limitations in dealing with the most challenging problems, which require an innovative approach to proof generation and theorem application.

Future Directions and Conclusion

LeanGeo sets the foundation for future research in automated geometry theorem proving by providing a robust framework and comprehensive benchmarks. Future work may focus on enhancing the automation and scalability of LeanGeo, integrating more sophisticated proof tactics, and augmenting its theorem library to further refine its capability.

In conclusion, LeanGeo represents a significant step towards unified and rigorous geometric reasoning systems, promoting deeper exploration into the intersection of geometry and other mathematical fields within proof assistants like Lean.