Gold-medalist Performance in Solving Olympiad Geometry with AlphaGeometry2 (2502.03544v2)

Abstract: We present AlphaGeometry2, a significantly improved version of AlphaGeometry introduced in Trinh et al. (2024), which has now surpassed an average gold medalist in solving Olympiad geometry problems. To achieve this, we first extend the original AlphaGeometry language to tackle harder problems involving movements of objects, and problems containing linear equations of angles, ratios, and distances. This, together with support for non-constructive problems, has markedly improved the coverage rate of the AlphaGeometry language on International Math Olympiads (IMO) 2000-2024 geometry problems from 66% to 88%. The search process of AlphaGeometry2 has also been greatly improved through the use of Gemini architecture for better language modeling, and a novel knowledge-sharing mechanism that enables effective communication between search trees. Together with further enhancements to the symbolic engine and synthetic data generation, we have significantly boosted the overall solving rate of AlphaGeometry2 to 84% for $\textit{all}$ geometry problems over the last 25 years, compared to 54% previously. AlphaGeometry2 was also part of the system that achieved silver-medal standard at IMO 2024 https://dpmd.ai/imo-silver. Last but not least, we report progress towards using AlphaGeometry2 as a part of a fully automated system that reliably solves geometry problems directly from natural language input.

• The paper introduces AlphaGeometry2, which surpasses gold medalist performance by expanding its domain language and adding new predicate syntaxes.
• It employs an improved DDAR2 symbolic engine and integrates the Gemini language model, achieving 88% coverage on IMO geometry problems.
• The research demonstrates significant computational efficiency, solving 42 out of 50 IMO problems through advanced automated reasoning.

Gold-medalist Performance in Solving Olympiad Geometry with AlphaGeometry2

The paper "Gold-medalist Performance in Solving Olympiad Geometry with AlphaGeometry2" (2502.03544) introduces AlphaGeometry2 (AG2) as an advanced enhancement over its predecessor, AlphaGeometry (AG1), in solving problems from the International Mathematical Olympiad (IMO) geometry category. AG2 reportedly surpasses the performance of an average gold medalist by employing a hybrid approach that leverages a robust LLM coupled with an improved symbolic engine. This essay examines the critical aspects of the research, providing an analysis of the advances in LLMs, domain-specific languages, and search algorithms. It concludes by exploring the implications of this research for the future of AI-driven problem-solving.

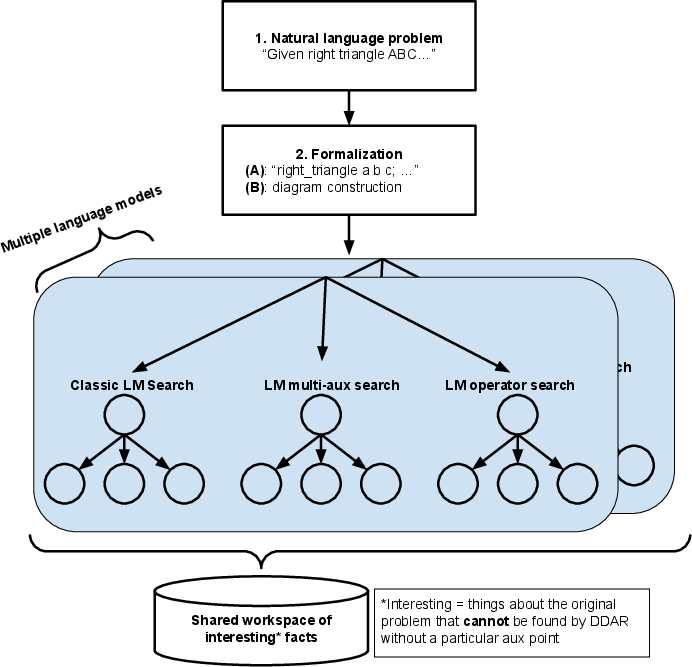
Figure 1: Overview of our search algorithm. We employ several different search trees which can share facts they proved via a special knowledge sharing mechanism.

Enhancements in AlphaGeometry2

Expanded Domain Language

The original AlphaGeometry model (AG1) was constrained by its limited domain-specific language, which restricted it to solving 66% of IMO geometry problems. The successor, AG2, overcame these limitations by expanding its domain language to cover problems involving locus-type theorems and linear equations of angles, ratios, and distances. AG2 now accommodates more advanced geometric concepts and relationships, achieving 88% coverage on IMO 2000-2024 geometry problems (Figure 2).

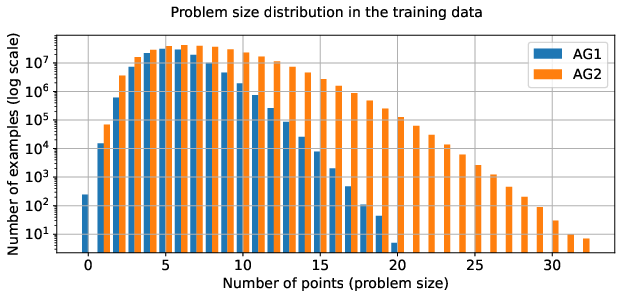
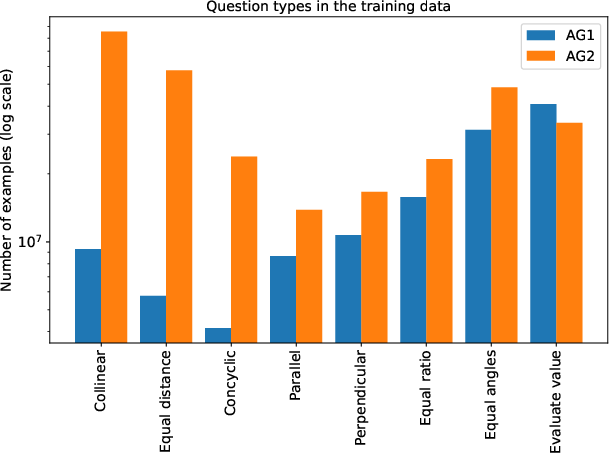
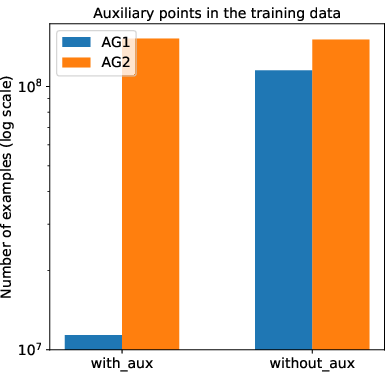
Figure 2: AG2 includes more complicated/longer problems compared to AG1.

To address additional categories that were not supported in AG1, AG2 incorporates new predicate syntaxes that can express locus-type statements, handle double points, and allow non-constructive problem descriptions (Figure 3). This flexibility considerably increases the scope of problems that AG2 can tackle, lifting domain language coverage from 66% (in AG1) to 88% for IMO problems.

Figure 3: Handling ``double" points in AG2. It is hard to prove that the intersection of $a$, $b$ is on $\omega$. But if a LLM suggests a construction $X' \in a \cap \omega$, then DDAR can prove the goal by proving $X' \in b$, and hence $X = X'$.

Enhanced Symbolic Engine: DDAR2

The symbolic engine, referred to as DDAR (Deductive Database Arithmetic Reasoning), underwent considerable improvements in AG2. DDAR computes the deduction closure through a predefined set of rules and follows a systematic process to add facts iteratively until no more can be added. Its primary limitations in AG1 were an inability to handle problems involving double points, a slower processing algorithm, and time-consuming implementation.

The new version, DDAR2, introduces a capability for handling double points. This makes proving complex theorems involving intersecting lines greatly streamlined.

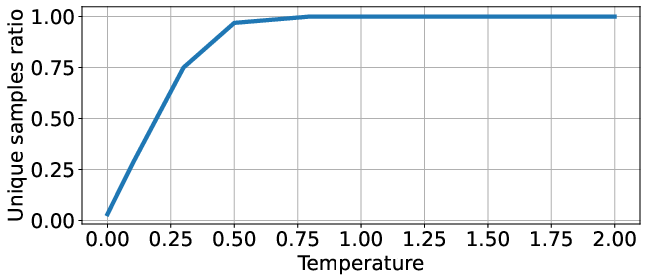
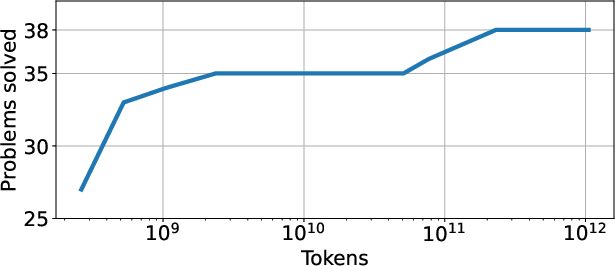
Figure 4: Ratio of unique samples for various temperatures for top-k sampling.

In terms of efficiency, DDAR2 implements a more efficient algorithm for proof search, reducing the complexity dramatically from $O(N^8)$ down to a more manageable cubic complexity in certain aspects of its computation, like the search for similar triangles and cyclic quadrilaterals. This offers a substantial reduction in computation time and accelerates the deduction closure process under the geometry problem-solving paradigm employed by AG2.

The Gemini LLM

In AG2, a more powerful LLM built upon the Gemini architecture is implemented. Unlike AG1, which utilized a simplified transformer trained in a two-phase approach, AG2 benefits from a single-phase training on an expanded dataset of 300 million synthetic problems. With the Gemini architecture, AG2 achieves considerable improvements in training efficiency and model performance, as demonstrated in the learning curves for various model sizes (Figure 5).

Experiments with different inference setups demonstrated that a higher temperature and more samples are essential to maximizing the IMO problem-solving success rate. Notably, top-k sampling with $t=1.0$ and we consistently observed that increasing the model size results in a decrease in perplexity and an improvement in performance.

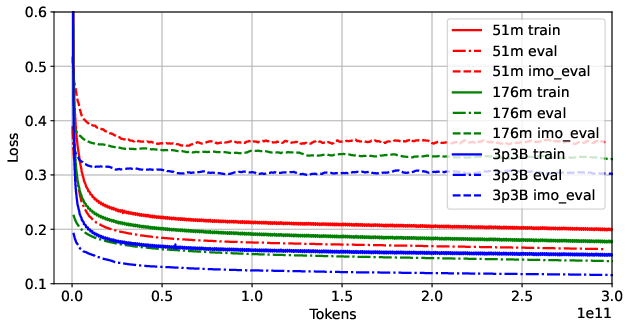
Figure 5: Learning curves for AlphaGeometry2 LLMs of different sizes in terms of parameter count ("m" - million, "B" - billion). Increasing the model size results in decreasing loss for train, eval and IMO evaluation sets.

A critical novel augmentation is the comprehensive generation of synthetic training data. Enhanced synthetic data generation, supplemented by auxiliary point construction and extensive dataset diversification, improves the model's performance significantly, boosting the solve rate on challenging Olympiad problems.

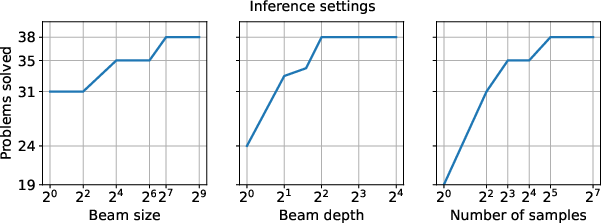
Figure 6: Number of 2000-2024 IMO geometry problems solved for different inference settings with one search tree. We start with beam size 512, beam depth 4, 32 samples and vary one of the parameters while keeping others fixed.

Performance Metrics and Outcomes

AlphaGeometry2 achieves a significant performance increase by solving 42 out of 50 geometry problems from IMO 2000-2024, a substantial improvement from AG1's previous best of 27 (Figure 7). The optimizer's new features, encompassing better problem formalization and enriched LLMs, played a key role in the achieved advancement. These results surpass an average gold medal level, setting a new standard for machine capabilities in solving competitive mathematics problems.

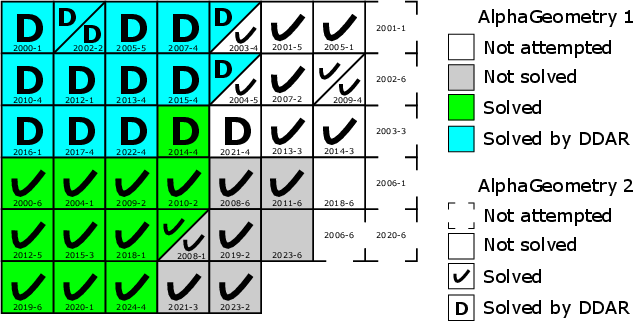
Figure 7: AlphaGeometry2 results on all 2000-2024 IMO geometry problems. Problems are grouped together based on their status, and ordered chronologically within the groups.

AlphaGeometry2 successfully emulates creative human-like approaches in problem solving by effectively employing non-traditional auxiliary constructions and sophisticated yet computationally viable geometry solving techniques. This proficiency extend beyond standard problem domains, automating the translation of natural language inputs into formal language, and comparable to the manual problem-solving capabilities seen in high-achieving human contestants.

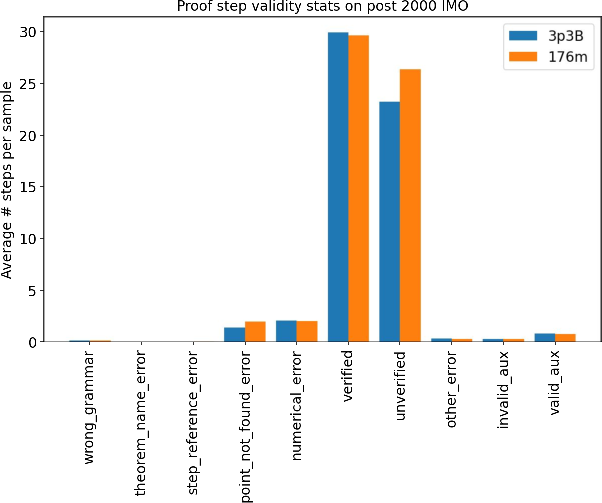
Figure 8: Proof steps validity statistics. Models almost do not make any syntax errors. Small and larger models perform similarly.

Conclusion

The development of AlphaGeometry2 represents a substantial upgrade in computational geometry problem solving capabilities, achieving and even surpassing an average gold medal performance. Its advancements in domain language, symbolic engine, and LLM integration have been pivotal in enhancing its solve rate on complex problems and in advancing automated formalization. However, further improvements to address current limitations, such as handling additional problem domains and enhancing auto-formalization, remain areas of future work to fully evolve the system's potential in automatic theorem proving and mathematical problem solving.