Layer Importance for Mathematical Reasoning is Forged in Pre-Training and Invariant after Post-Training (2506.22638v2)

Abstract: LLMs improve at math after instruction tuning, reinforcement learning, or knowledge distillation. We ask whether these gains come from major changes in the transformer layers or from smaller adjustments that keep the original structure. Using layer-wise ablation on base and trained variants, we find that math reasoning depends on a few critical layers, which stay important across all post-training methods. Removing these layers reduces math accuracy by as much as 80%, whereas factual recall tasks only show relatively smaller drops. This suggests that specialized layers for mathematical tasks form during pre-training and remain stable afterward. As measured by Normalized Mutual Information (NMI), we find that near these critical layers, tokens drift from their original syntactic clusters toward representations aligned with tokens less syntactically related but potentially more useful for downstream task.

• The paper demonstrates that specific transformer layers, such as Qwen’s layer 23 and Llama’s layers 15 and 18, are critical for mathematical reasoning, with ablation causing up to an 80% performance drop.
• The study employs zero-ablation experiments and NMI analysis to reveal that these critical layers, forged during pre-training, are invariant after post-training across different tasks.
• The findings suggest that targeted model fine-tuning and optimized transformer designs could enhance mathematical reasoning capabilities by preserving the function of these crucial layers.

Layer Importance for Mathematical Reasoning in Transformer Models

The paper "Layer Importance for Mathematical Reasoning is Forged in Pre-Training and Invariant after Post-Training" investigates whether the improvements in LLMs for mathematical reasoning arise from major structural changes during post-training or from minor adjustments to the pre-existing model architecture. The study employs layer-wise ablation experiments to analyze the significance of individual layers in the transformer architectures and assess how these critical layers contribute to both mathematical and non-mathematical tasks.

Methodology and Experiments

The core methodology involves systematic zero-ablation of layers within transformer models, specifically focusing on Qwen and Llama variants. The paper evaluates the models across mathematical reasoning benchmarks such as GSM8K and MATH500, alongside TriviaQA for factual recall tasks. Zero-ablation entails nullifying parameters of a specific transformer layer to examine the impact on model performance without altering the overall architecture due to residual connections.

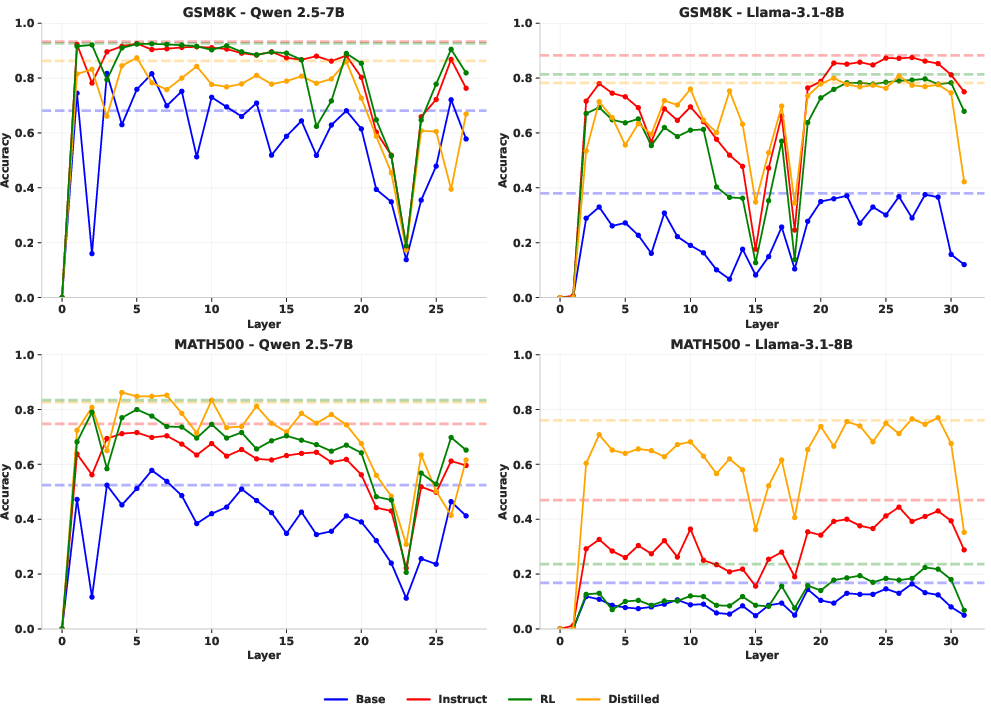
Figure 1: The plots show model accuracy (Y-axis) on GSM8K and MATH500 when a single transformer layer (X-axis) is zeroed out. The performance of all model variants drops substantially when specific layers are removed (layer 23 for Qwen, layers 15 and 18 for Llama), a pattern that remains consistent across different datasets and post-training methods. Dashed lines indicate the original, un-ablated performance.

Key Findings

Critical Layer Identification

The ablation studies reveal that models depend heavily on a few "critical" layers for mathematical reasoning tasks, evidenced by sharp performance declines—up to 80% in accuracy—when these layers are ablated. For Qwen models, layer 23 is pivotal, while Llama models demonstrate sensitivity at layers 15 and 18. Interestingly, these layers remain relevant irrespective of the post-training method applied, indicating their importance is instilled during pre-training.

Figure 2: Layer ablation results on the TriviaQA factual recall task. The left plot shows performance for Qwen 2.5-7B models, and the right plot shows performance for Llama 3.1-8B models when individual layers are zeroed out. The X-axis represents the layer index (0-32), and the Y-axis shows the accuracy.

Representational Shifts via NMI Analysis

The study employs Normalized Mutual Information (NMI) to analyze representational shifts across layers, providing insight into how token clustering evolves. In mathematical reasoning tasks, critical layers exhibit distinct representational transitions, with tokens forming semantically enriched clusters. This drift from syntactic tokens to semantically significant representations is measured by decreases in NMI scores nearing critical layers, indicating a potential correlation with their task-specific importance.

Figure 3: The plots show the NMI score (Y-axis) at each transformer layer (X-axis), calculated relative to the token clusters at Layer 0. The observed trends are robust to the number of clusters (k) used for the analysis, with similar results for k-values between 10 and 70. The choice of 50 here is arbitrary. Shaded region denotes standard deviation over 5 runs.

Limitations and Implications

This study's results are primarily derived from ablation and NMI analyses on Qwen and Llama models within a specific parameter range (7B-8B). Broader assessments across various model scales and architectures could enhance generalizability. Additionally, while NMI provides a high-level view of representational changes, it lacks the granularity to pinpoint specific reasoning mechanisms within models. Future work could explore fine-tuning strategies targeting identified critical layers to enhance efficiency in mathematical reasoning tasks or employ mechanistic interpretability for deeper insights.

Conclusion

The findings suggest a stable architecture for mathematical reasoning tasks that persists post-training, driven by a small number of critical layers. This stability contrasts with non-mathematical tasks like factual recall, where layer importance is more evenly distributed. These insights can inform future transformer model designs emphasizing layer configurability and task-specialization strategies. The research underscores the potential for optimizing LLMs' mathematical reasoning capabilities by focusing on the preservation and enhancement of these critical layers.