Scalable Machine Learning Algorithms using Path Signatures

Abstract: The interface between stochastic analysis and machine learning is a rapidly evolving field, with path signatures - iterated integrals that provide faithful, hierarchical representations of paths - offering a principled and universal feature map for sequential and structured data. Rooted in rough path theory, path signatures are invariant to reparameterization and well-suited for modelling evolving dynamics, long-range dependencies, and irregular sampling - common challenges in real-world time series and graph data. This thesis investigates how to harness the expressive power of path signatures within scalable machine learning pipelines. It introduces a suite of models that combine theoretical robustness with computational efficiency, bridging rough path theory with probabilistic modelling, deep learning, and kernel methods. Key contributions include: Gaussian processes with signature kernel-based covariance functions for uncertainty-aware time series modelling; the Seq2Tens framework, which employs low-rank tensor structure in the weight space for scalable deep modelling of long-range dependencies; and graph-based models where expected signatures over graphs induce hypo-elliptic diffusion processes, offering expressive yet tractable alternatives to standard graph neural networks. Further developments include Random Fourier Signature Features, a scalable kernel approximation with theoretical guarantees, and Recurrent Sparse Spectrum Signature Gaussian Processes, which combine Gaussian processes, signature kernels, and random features with a principled forgetting mechanism for multi-horizon time series forecasting with adaptive context length. We hope this thesis serves as both a methodological toolkit and a conceptual bridge, and provides a useful reference for the current state of the art in scalable, signature-based learning for sequential and structured data.

• The paper introduces variational inference and low‐rank tensor projections to overcome computational bottlenecks in signature-based methods.
• It demonstrates enhanced performance in GP, deep learning, and GNN frameworks across diverse datasets with improved calibration and prediction.
• The work extends path signatures to graph domains using randomized kernel approximations and hypo-elliptic diffusions for robust feature extraction.

Scalable Machine Learning with Path Signatures: Algorithms, Theory, and Applications

Introduction and Motivation

This work presents an exhaustive, technically rigorous study on the integration of path signatures—a fundamental concept from rough path theory—into scalable machine learning algorithms for sequential, temporal, and graph-structured data (2506.17634). Path signatures provide universal, hierarchical, and algebraically rich representations of paths and sequences, enabling powerful invariance and expressivity. However, direct computation of signature features and their kernelizations incurs severe computational bottlenecks, both due to the combinatorial explosion in feature space and the quadratic scaling in sample size and sequence length. This manuscript addresses these bottlenecks through algorithmic, variational, and randomized constructions, establishing new scalable, theoretically analyzable machine learning methods.

Algebraic and Analytic Foundations

Path signatures are constructed via the tensor algebra over a feature space $V$. For a discretized path or sequence, the signature is an infinite sequence of tensors, with the $m$-th term encoding all non-contiguous $m$-subsequences in the data. Central algebraic properties, such as the non-commutative product and shuffle product, ensure that path signatures capture order, concatenation, and symmetries relevant for temporal modeling. Crucially, the signature is universal in the sense of the Stone–Weierstrass theorem: any continuous function on paths can be uniformly approximated by a linear functional of the signature truncated to finite degree. The signature map is injective up to reparameterization or tree-like equivalence, providing robust invariances. These properties collectively establish the theoretical suitability of path signatures across a vast set of sequential domains.

Scalable Gaussian Processes with Signature Kernels

The first major scalable Bayesian approach extends GPs with signature kernels, embedding sequential data in a signature feature space with a signature-based covariance (Sections "Gaussian Processes with Signature Covariances"). A key technical advance is the development of variational inference based on "inducing tensors" in the feature space, yielding inter-domain sparse GP inference that scales sub-cubically in the number of sequences and linearly in sequence length. This approach generalizes sparse GPs with pseudo-inputs, permitting the inducing variables to be structured elements of the tensor algebra rather than sequences themselves. On a comprehensive suite of time series classification tasks, signature GP models consistently achieve lowest negative log-predictive probability (NLPP) and high accuracy across data modalities (Figure 1). Notably, these models outperform all classical GP sequence models in both calibration and prediction, and are competitive with modern deep TSC baselines.

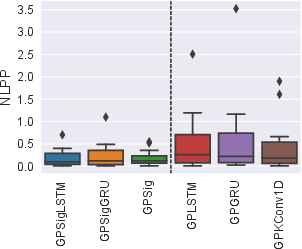
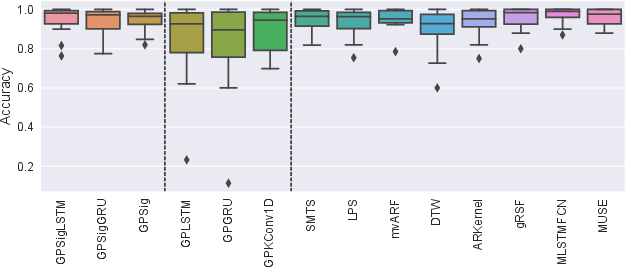
Figure 1: Box-plots of negative log-predictive probabilities (left) and classification accuracies (right) on 16 TSC datasets.

Deep Low-Rank Tensor Architectures: Seq2Tens and Deep S2T Layers

Recognizing the computational intractability of full signature tensors, the Seq2Tens framework introduces highly scalable, low-rank projection methods for signature-based modeling in neural architectures. By parameterizing dual functionals on the signature via collections of low-rank or recursive rank-1 tensors, these projections can be evaluated with runtime linear in sequence length and tensor degree, leveraging dynamic programming. Crucially, although individual low-rank functionals are less expressive, stacking multiple seq2seq layers (akin to deep networks) restores functional universality, as demonstrated algebraically and empirically. These layers are compatible with convolutional, recurrent, or feedforward preprocessing, and particularly effective when used in bidirectional setups.

On multivariate TSC tasks, models combining convolutional feature extractors and stacked S2T layers match or exceed state-of-the-art deep learning and classical baselines, with significant reductions in parameter count and computation. A prominent outcome is that low-rank signature projections, when composed, empirically recover the expressivity of full signature kernels but with practical tractability (see Figure 2).

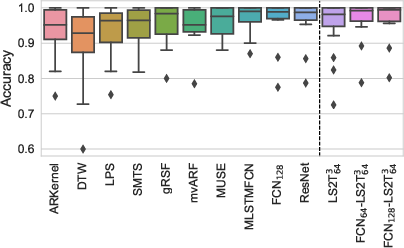
Figure 2: Box-plot of classification accuracies (left) and critical difference diagram (right).

Path Signatures for Graph Learning: Hypo-Elliptic Diffusions on Graphs

To extend signature-based reasoning to graph domains, the manuscript introduces hypo-elliptic diffusion processes and tensor-valued Laplacians defined via random walks and path signatures over graphs. By constructing matrix rings over the tensor algebra, the framework provably summarizes distributions of random walk histories as nodes' or graphs' features, capturing both local and global, long-range dependencies. These features are then projected via low-rank functionals, recursively composed (Figure 3), and used in GNN-type architectures with or without attention.

Empirically, this approach substantially outperforms classical and hierarchical GNNs on biochemical graph classification, especially on tasks requiring long-range and global structure (NCI1/NCI109). The method eliminates the need for full pairwise node interactions (unlike transformer-based models), retains locality of influence distributions, and is robust to pooling/squashing phenomena. The computational complexity grows linearly with respect to edges and tensor rank, enabling efficient processing on large graphs.

Figure 3: Visualization of the architecture used for NCI1 and NCI109 described in Section 4.2.

Random Fourier Signature Features: Scalable Kernelization and Approximation

A critical bottleneck for signature kernel methods is their quadratic scaling in both sample size and sequence length. The manuscript introduces Random Fourier Signature Features (RFSF): random feature maps producing unbiased, exponentially-concentrating approximations to the signature kernel. The construction leverages a Bochner-type Fourier analytic perspective applied to the signature kernel, but over the nonlinear, tensorial domain of sequences. By independently randomizing each degree-$m$ term, RFSF achieves uniform convergence in probability, with explicit finite-sample rates (Figure 4).

Dimensionality reduction strategies, including diagonal projections (RFSF-DP) and tensor random projections (RFSF-TRP), further reduce complexity and memory, making state-of-the-art signature kernels feasible on datasets with $10^6$ or more sequences. Experimentation demonstrates that these random feature kernels provide accuracy and calibration essentially indistinguishable from the exact kernel, and in many regimes outperform prior random feature baselines (e.g., random warping series) by substantial margins.

Figure 4: Approximation error of random kernels against RFF size on log-log plot.

Recurrent Sparse Spectrum Signature GPs: Adaptive Forecasting with Forgetting

Building on scalable signature feature approximations, the RS$^3$GP model combines random Fourier decayed signature features with GP inference and a learnable forgetting mechanism. Exponential decay parameters governing context adaptivity are optimized via variational inference, enabling the model to automatically interpolate between short- and long-term temporal dependencies for forecasting tasks. High-throughput GPU kernelization and work-efficient parallel scans render the approach effective for high-dimensional, long-horizon time series (Figure 5).

On standard forecasting benchmarks (Solar, Electricity, Wikipedia, etc.), RS$^3$GP achieves probabilistic forecasting performance matching or superseding deep learning baselines (e.g., TSDiff, DeepAR) and does so with dramatically reduced training time and computational resources. CRPS is minimized on long-range datasets, and uncertainty quantification is calibrated.

Figure 5: Computation time (left) and memory consumption (right) of VRS$^3$GP (variational recurrent sparse spectrum signature GP) scaling with sequence length.

Visualizing Expressivity and Scalability

The expressivity, optimization, and learned manifold structure of signature-based models are visualized using low-dimensional embeddings of learned signature tensors and inducing points. UMAP projections on high-class-count multivariate sequential datasets show that inducing tensors populate distinct subspaces from underlying data—contradicting standard GP intuition that inducing points should gravitate toward classification boundaries in data space and confirming the higher expressivity afforded by the tensor algebra (Figure 6). Experiments also quantify accuracy and ELBO progress as the number of inducing tensors varies, demonstrating their practical data efficiency relative to sequence-based inducing points (Figure 7).

Figure 7: Achieved ELBO (top), accuracy (middle), mean NLPP (bottom) after 300 epochs of training the variational parameters with random initialization and frozen pre-learnt kernel hyperparameters. Solid is the mean over 5 independent runs, dashed is the 1-std region.

Figure 6: A UMAP visualization of the features corresponding to data-points (coloured), and inducing tensors (black) in the feature space on the AUSLAN dataset.

Theoretical and Practical Implications

This body of work establishes path signatures as a theoretically universal and practically scalable class of representations for sequential and structured data, via:

• Novel variational inference machinery over the tensor algebra for tractable GPs.
• Deep, low-rank tensor functionals recovering universality with linear complexity.
• Algebraically principled extension to graph domains, capturing non-local and global structure beyond classical GNN capabilities.
• Randomized, unbiased kernel approximations enabling scaling to orders-of-magnitude larger datasets without loss of accuracy.
• Data-driven, variational forgetting and adaptive context modeling for temporal prediction.

The results highlight path signatures' compatibility with both probabilistic and deep learning scenarios, and their suitability for settings demanding explicit, provable invariances.

Outlook and Future Directions

The methods developed here suggest a path for scalable structured data machine learning with theoretical underpinning and operational feasibility. Possible future research includes:

• Higher-order signature kernel approximation and random feature theory, addressing the full geometric signature beyond order-1 features.
• Deeper exploration of stacked low-rank signature layers' universality and connection to the neural tangent kernel regime.
• Expansion of hypo-elliptic diffusion and signature GNNs to higher-order network topologies, such as simplicial and cellular complexes.
• Further algorithmic acceleration via structured or block-orthogonal random features.
• Enhanced interpretability via signature inversion and saliency, and further development of signature-based statistical tests.

Conclusion

This work demonstrates that, through rigorous algorithmic innovation and theoretical analysis, it is feasible to unlock the algebraic and analytic potential of path signatures for scalable, expressive, and invariant machine learning on sequential and structured data. The approaches documented herein position signature-based methods as essential primitives for future probabilistic, deep, and kernel-based learning systems in artificial intelligence and scientific data analysis (2506.17634).