The Principles of Diffusion Models (2510.21890v1)
Abstract: This monograph presents the core principles that have guided the development of diffusion models, tracing their origins and showing how diverse formulations arise from shared mathematical ideas. Diffusion modeling starts by defining a forward process that gradually corrupts data into noise, linking the data distribution to a simple prior through a continuum of intermediate distributions. The goal is to learn a reverse process that transforms noise back into data while recovering the same intermediates. We describe three complementary views. The variational view, inspired by variational autoencoders, sees diffusion as learning to remove noise step by step. The score-based view, rooted in energy-based modeling, learns the gradient of the evolving data distribution, indicating how to nudge samples toward more likely regions. The flow-based view, related to normalizing flows, treats generation as following a smooth path that moves samples from noise to data under a learned velocity field. These perspectives share a common backbone: a time-dependent velocity field whose flow transports a simple prior to the data. Sampling then amounts to solving a differential equation that evolves noise into data along a continuous trajectory. On this foundation, the monograph discusses guidance for controllable generation, efficient numerical solvers, and diffusion-motivated flow-map models that learn direct mappings between arbitrary times. It provides a conceptual and mathematically grounded understanding of diffusion models for readers with basic deep-learning knowledge.
Sponsor
Paper Prompts
Sign up for free to create and run prompts on this paper using GPT-5.
Top Community Prompts
Explain it Like I'm 14
What is this paper about?
This paper is a friendly, big-picture guide to diffusion models—AI systems that can create things like images, sounds, or text by gradually turning random noise into something meaningful. The authors explain where these models came from, how they work, why there are different “versions” of them, and how all those versions are actually connected by the same core idea.
What questions does it try to answer?
The paper focuses on a few simple questions:
- How do diffusion models turn noise into realistic data step by step?
- Why are there three popular ways to think about them (variational, score-based, and flow-based), and how are those ways connected?
- How can we guide a diffusion model to follow a user’s wishes (for example, “draw a cat on a skateboard”)?
- How can we make sampling (the process of generating results) faster and more efficient?
- What math sits under the hood, and how does it help us design better models?
How do the methods work? A simple tour
The authors explain diffusion models using everyday ideas and three complementary viewpoints. First, an overall picture:
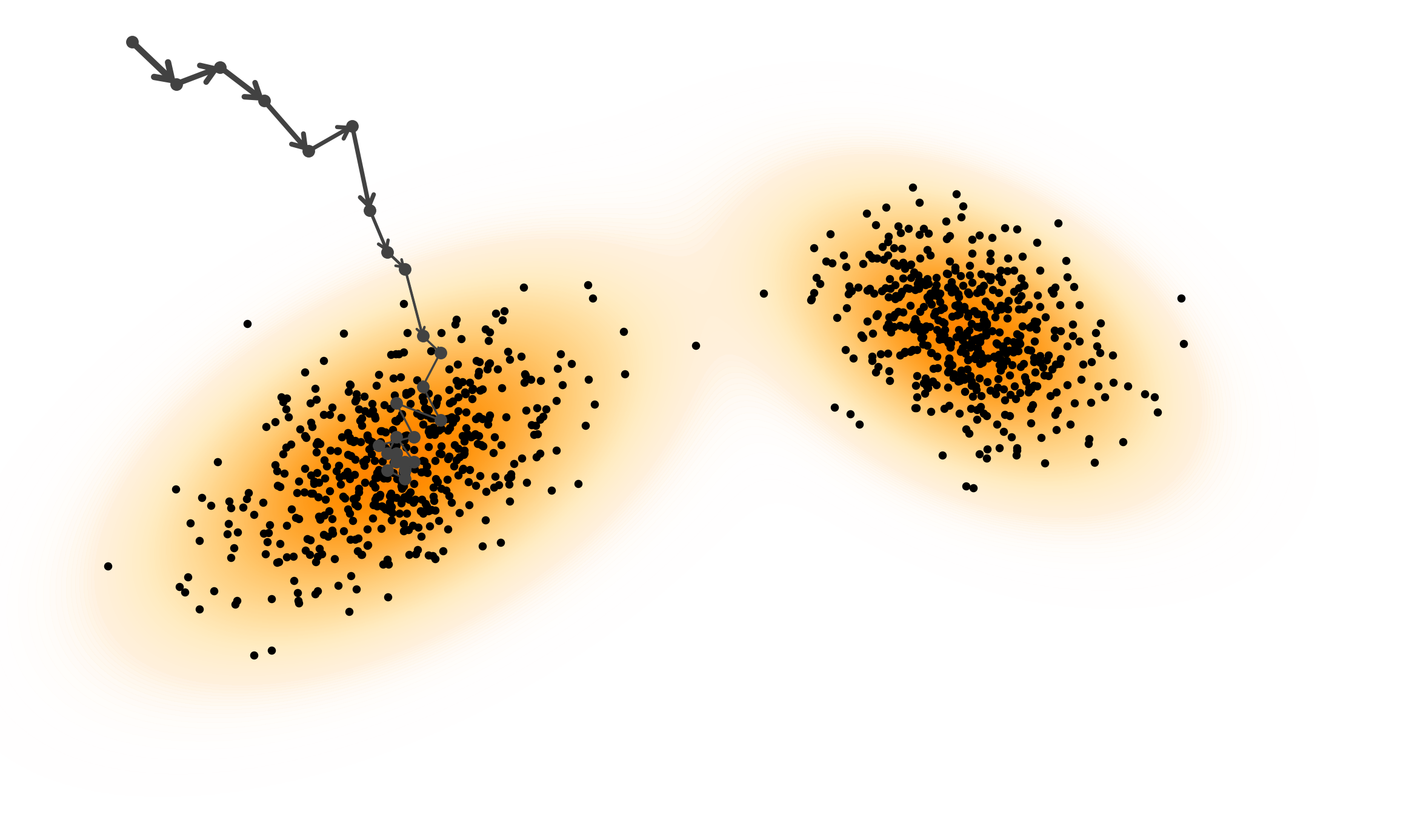
- Imagine starting with a clear photo. You slowly add noise (like fog), making it blurrier and blurrier until it looks like pure static. That’s the “forward process.”
- The goal is to learn the reverse: starting from pure noise (static), remove the fog a little at a time until you get a clean, realistic image. That’s the “reverse process.”
Here are the three ways to formalize that reverse process:
- Variational view (think “cleaning tiny bits at a time”):
- Analogy: You clean a dirty window layer by layer. Each small cleaning step teaches the model how to remove a little noise.
- In practice: The model learns to denoise in small steps, and stacking many small successes creates a full image from noise.
- Score-based view (think “follow the slope to the best place”):
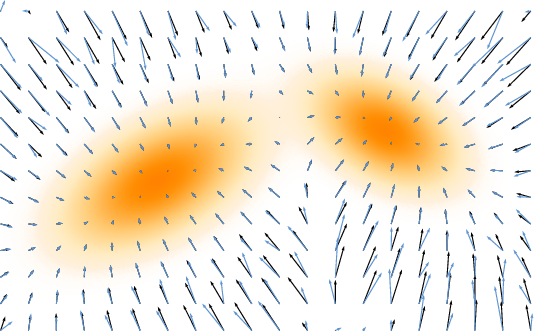
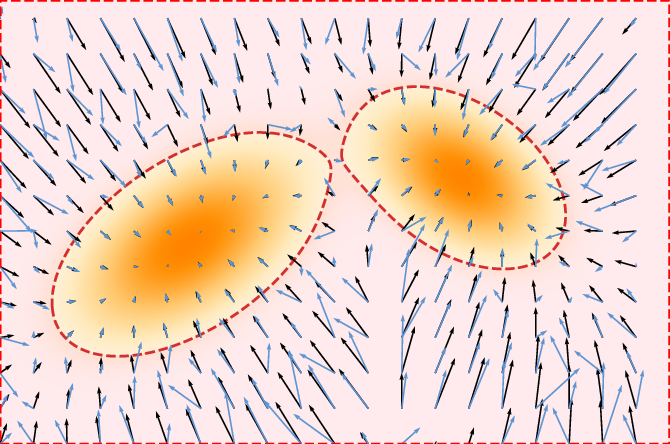
- Analogy: Picture a landscape where high ground means “more likely to be real.” The “score” is a vector that tells you which direction goes uphill. Starting from random points, you climb toward likely, realistic results.
- In practice: The model learns the gradient (direction of steepest increase) of the data’s likelihood, then uses it to push noisy samples toward realistic ones. This can be described with differential equations (continuous rules for moving through time).
- Flow-based view (think “smooth path with a guiding wind”):
- Analogy: Imagine a gentle wind (a velocity field) that blows random particles along a path until they form a realistic image. If you follow the wind over time, you arrive at the data.
- In practice: The model learns a velocity field that transports noise to data smoothly using an ordinary differential equation (ODE).
All three share the same backbone: a time-dependent “velocity field” that tells samples how to move from noise to data. Generating a sample is like solving a step-by-step instruction manual (a differential equation) that transforms noise into something meaningful.
What did the authors show, and why does it matter?
Here are the main takeaways the paper organizes and clarifies:
- The three views are deeply connected:
- Even though they look different, they describe the same journey from noise to data using the same underlying math. This connection is explained using tools like the Fokker–Planck equation (think: rules for how a crowd of particles spreads and concentrates over time).
- Guidance makes generation controllable:
- You can steer the model to follow instructions (like text prompts) by adding a gentle “nudge” during sampling. This is how text-to-image models draw what you ask for.
- Faster sampling is possible:
- The usual process takes many small steps (slow). The paper explains better numerical solvers that take fewer, smarter steps while keeping quality high.
- Even faster models can be learned:
- Distillation: Train a smaller or simpler “student” to mimic a slower “teacher” diffusion model, but with far fewer steps.
- Flow maps: Learn a direct jump from one time to another along the generative path, sometimes even going from noise to data in one or a few jumps.
- Connections to classic math:
- The paper links diffusion models to optimal transport and the Schrödinger bridge (ideas about moving probability mass in the most efficient or well-regularized way). This helps ground the field in well-studied theory and suggests new methods.
Why it matters: Understanding that all these methods are variations of the same core principle helps researchers design better, faster, and more controllable generative models with confidence.
What could this change or enable?
- Better tools for creators: Faster, higher-quality generation of images, audio, and video that can follow instructions more precisely.
- Smarter controls: More reliable ways to steer models (e.g., safety, style, or preference alignment), making generative AI more useful and trustworthy.
- Efficient systems: Methods that cut down the time and compute needed to sample, making powerful generation available on smaller devices.
- Strong theory, better practice: The unified view and math connections give a sturdy foundation for future research, helping new ideas build on what’s already known instead of reinventing the wheel.
In short, this paper serves as a clear map of the diffusion-model landscape: it shows how the main ideas fit together, how to guide and speed up these models, and how solid math supports it all.
Knowledge Gaps
Knowledge gaps, limitations, and open questions
Below is a concise list of what this monograph leaves missing, uncertain, or unexplored, framed as concrete, actionable directions for future research.
- Formal equivalence under discretization: Precisely characterize when variational, score-based, and flow-based formulations yield the same generative trajectory in discrete time with finite-capacity networks and imperfect training, and provide counterexamples where they diverge.
- Forward corruption design beyond Gaussian noise: Systematically paper non-Gaussian, data-adaptive, or geometry-aware forward processes and schedules, and quantify their impact on training stability, sample quality, controllability, and solver efficiency.
- Convergence and stability guarantees: Derive bounds on how score/velocity estimation errors propagate through reverse-time SDE/ODE sampling, including conditions for convergence to the target distribution and stability regions for practical samplers.
- Numerical solver error analysis: Develop rigorous step-size–error trade-offs, adaptive schemes, and stability criteria for fast ODE/SDE samplers, especially under model misspecification and guidance, with provable quality guarantees.
- Guidance correctness and calibration: Establish when classifier(-free) and preference-based guidance preserves calibrated likelihoods or target marginals; quantify the trade-off between conditioning strength, realism, diversity, and faithfulness to prompts.
- Preference alignment objectives: Design and evaluate principled training objectives and metrics for aligning diffusion models with human or task preferences without collapsing diversity or introducing artifacts.
- Distillation theory for few-step generators: Provide distributional error bounds and sample-complexity analyses for distilling slow diffusion samplers into few-step or single-step generators, including minimal steps needed to meet quality targets.
- Consistent flow-map learning: Ensure semigroup/composition consistency for “anytime-to-anytime” flow maps; develop training objectives and diagnostics that prevent time-inconsistent mappings and quantify composition error.
- Discrete and hybrid data modalities: Extend the framework to discrete spaces (e.g., text, graphs) via jump processes or hybrid continuous–discrete formulations, and analyze reverse-time dynamics and solvability in these settings.
- Optimal transport and Schrödinger bridge links: Make explicit the conditions under which learned velocity fields coincide with OT/SB solutions; paper the role of entropy regularization, non-Gaussian priors, and sample-based estimators in practice.
- Identifiability and sample complexity: Determine when the score or velocity field is uniquely recoverable from finite data; derive generalization rates and regularization strategies that guarantee consistent recovery.
- Evaluation and benchmarking gaps: Establish standardized, modality-agnostic metrics for quality, diversity, controllability, and efficiency, and conduct systematic cross-method comparisons the monograph intentionally avoids.
- Robustness and safety: Analyze sensitivity to guidance perturbations, out-of-distribution inputs, and adversarial attacks; develop principled constraint mechanisms (e.g., safety filters) that preserve theoretical guarantees.
- Scaling laws and efficiency: Investigate compute–data–architecture scaling laws specific to diffusion/flow models and identify training regimes and curricula that optimize performance per unit cost.
- Architectural priors for velocity fields: Explore parameterizations that embed symmetries, conservation laws, or physics-informed constraints, and quantify their effect on sample quality, training dynamics, and theoretical properties.
- Practical deployment constraints: Bridge theory with system-level concerns (memory, latency, hardware accelerators) by designing samplers and model variants tailored to real-world deployment while retaining principled guarantees.
Practical Applications
Immediate Applications
Below are deployable applications that draw directly from the monograph’s unified principles of diffusion models (variational, score-based, and flow-based views), guidance mechanisms, advanced numerical solvers, and distillation/flow-map acceleration.
- Controllable text-to-image, audio, and video generation via guidance (Media/Software)
- Description: Use classifier and classifier-free guidance to steer generative trajectories toward user-specified attributes and preferences.
- Potential tools/workflows: Prompting UIs with adjustable guidance scales; preference datasets; API endpoints that expose guidance weight schedules; batch sampling with fixed ODE integrators.
- Assumptions/dependencies: High-quality pretrained diffusion backbones; representative and well-curated preference datasets; compute (GPU/TPU); safety filters tuned to guidance levels.
- Image restoration and enhancement with diffusion priors (Imaging/Consumer apps)
- Description: Super-resolution, deblurring, denoising, inpainting, and colorization by treating reconstruction as guided reverse-time denoising or plug-and-play score-based priors.
- Potential tools/workflows: Photo editing plugins; batch restoration pipelines; integration with camera apps for post-processing; “noise-to-clean” sliders (anytime-to-anytime jumps).
- Assumptions/dependencies: Accurate forward degradation models (blur/noise); domain-matched training; robust numerical solvers to prevent artifacts in few-step sampling.
- Synthetic data generation for privacy-preserving analytics (Healthcare, Finance, Retail; Policy)
- Description: Generate realistic but non-identical samples that preserve statistical properties of sensitive datasets to support analytics and prototyping.
- Potential tools/workflows: Synthetic cohort generators; structured/text/image tables; evaluation dashboards for utility/privacy trade-offs.
- Assumptions/dependencies: No formal privacy guarantees by default; requires rigorous utility and reidentification testing; compliance and governance processes.
- Fast inference via advanced numerical solvers (Software/ML platforms)
- Description: Replace many-step samplers with high-order ODE solvers and tailored schedules to reduce latency while preserving quality.
- Potential tools/workflows: Solver libraries (adaptive step, multi-step methods); model-card guidance on stable step counts; A/B testing for quality vs. speed.
- Assumptions/dependencies: Stability and error control under aggressive step reduction; solver hyperparameters tuned to model and modality.
- On-device content creation with distilled generators (Mobile/Edge)
- Description: Distill slow teacher diffusion models into few-step or one-step students for real-time creation of images, stickers, and audio effects.
- Potential tools/workflows: Lightweight runtimes (Metal/Vulkan/NNAPI); quantization-aware distillation; streaming generation with partial trajectories.
- Assumptions/dependencies: Teacher quality and coverage; memory/compute constraints; edge safety policies; robustness across diverse device hardware.
- Preference-guided, aligned generation (Safety/Policy; Media)
- Description: Incorporate preference datasets to steer outputs toward acceptable or desired styles (e.g., reducing toxicity, reinforcing brand look).
- Potential tools/workflows: Guidance pipelines with preference losses; dashboards to tune alignment weights; human-in-the-loop reviews.
- Assumptions/dependencies: Preference data quality and representativeness; monitoring for unintended bias; transparent governance and auditability.
- Flow-matching for domain/style translation (Design/Healthcare Imaging)
- Description: Learn velocity fields that transport source distributions to target distributions (e.g., artistic style transfer; research-grade CT↔MRI synthesis).
- Potential tools/workflows: Paired/unpaired domain-transfer training; inference “source-to-target” batches; editors with domain sliders.
- Assumptions/dependencies: Sufficient domain coverage; evaluation for anatomical fidelity (medical use); regulatory constraints for clinical deployment.
- Anytime-to-anytime latent editing via learned flow maps (Creative tools)
- Description: Jump along the generative trajectory to perform targeted edits (e.g., adjust texture/detail without full resampling).
- Potential tools/workflows: Latent timeline controls; “refine” vs. “coarsen” toggles; partial-trajectory caching.
- Assumptions/dependencies: Accurate flow-map estimation across times; edit consistency; user interface clarity around stochastic vs. deterministic behavior.
- Audio denoising and speech synthesis with diffusion (Audio engineering, Accessibility)
- Description: Use diffusion-based denoisers and TTS systems for clean speech, voice cloning consented datasets, and accessibility features.
- Potential tools/workflows: DAW plugins; real-time noise removal; text-to-speech with guidance for prosody/style.
- Assumptions/dependencies: Quality datasets; latency constraints; ethical use (voice cloning permissions).
- Robotics planning with guided generative policies (Robotics)
- Description: Sample feasible trajectories under constraints using guided diffusion policies as priors in offline planning or model-predictive control.
- Potential tools/workflows: Integrations with simulators; constraint-aware guidance terms; motion libraries built from generative trajectories.
- Assumptions/dependencies: Accurate dynamics models or simulators; sim-to-real transfer; safe exploration and verification.
- Inverse problems with score-based priors (e.g., MRI/CT reconstruction) (Healthcare/Scientific imaging)
- Description: Combine physical forward models with learned diffusion priors for reconstruction in low-signal regimes or accelerated acquisitions.
- Potential tools/workflows: Reconstruction toolkits; plug-in priors with tunable regularization; validation on phantom and clinical data.
- Assumptions/dependencies: Well-specified measurement models; clinical validation; regulatory review for diagnostic use.
- Curriculum and training materials (Academia/Education)
- Description: Use the monograph to teach unified foundations (Fokker–Planck, continuity, SDE/ODE) and connect variants (DDPM, Score SDE, Flow Matching).
- Potential tools/workflows: Lecture modules; interactive notebooks with solver demos; assignments on guidance and acceleration.
- Assumptions/dependencies: Students with basic deep learning background; access to small-scale compute for demos.
Long-Term Applications
These applications are feasible with further research, scaling, clinical validation, provable guarantees, or system-level engineering. They build on the monograph’s emphasis on velocity fields, transport, and accelerated flow maps.
- Data assimilation via Schrödinger bridges and flow matching (Climate/Weather, Energy)
- Description: Use entropy-regularized optimal transport to merge observations with priors, transporting probability mass to match real-time measurements.
- Potential tools/workflows: Generative assimilation modules; uncertainty-aware transport solvers; HPC integration.
- Assumptions/dependencies: Rich, timely sensor data; stable training at scale; rigorous uncertainty quantification.
- Real-time on-device video generation and editing (Mobile AR/VR)
- Description: One- or few-step video diffusion on consumer devices for interactive, coherent frames with controllable guidance.
- Potential tools/workflows: Specialized accelerators; temporal flow-map distillation; consistent multi-frame solvers.
- Assumptions/dependencies: Hardware advances; temporal consistency guarantees; energy/thermal budgets.
- Formally safe, constraint-satisfying generative control (Policy/Robotics/Software)
- Description: Integrate guidance with formal constraints (e.g., barrier certificates) to guarantee safe outputs/trajectories.
- Potential tools/workflows: Hybrid verification + sampling; certified solvers; runtime monitors.
- Assumptions/dependencies: Mature verification frameworks for stochastic flows; tractable certification; sector-specific safety standards.
- Clinically validated synthetic cohorts and training data (Healthcare)
- Description: Diffusion-generated synthetic medical images/patient records for training, with proven diagnostic utility and privacy robustness.
- Potential tools/workflows: Validation pipelines; blinded reader studies; bias audits; regulatory submissions.
- Assumptions/dependencies: Strong utility evidence; reidentification risk assessment; multi-institutional collaboration.
- Scenario generation and stress testing in finance (Finance/Risk)
- Description: Flow-based generators conditioned on macro/market covariates to produce stress scenarios under distributional constraints.
- Potential tools/workflows: Scenario libraries; tail-focused guidance; audit trails for regulatory review.
- Assumptions/dependencies: Model risk management; alignment with supervisory expectations; robust backtesting.
- Universal flow-map services (Software/Platforms)
- Description: Deploy general-purpose learned flow maps that jump between arbitrary times and domains for rapid prototyping across tasks.
- Potential tools/workflows: “Flow-as-a-service” APIs; time-conditioned models; composite guidance stacks.
- Assumptions/dependencies: Broad generalization across modalities; composability; versioning and reproducibility.
- Multi-modal controllable generation with unified velocity fields (Media/Metaverse)
- Description: Joint text–image–audio–3D generation with consistent conditioning and guidance terms across modalities.
- Potential tools/workflows: Cross-modal adapters; joint solvers; preference datasets spanning modalities.
- Assumptions/dependencies: Scalable multi-modal training; consistent alignment objectives; evaluation across modalities.
- Governance standards for synthetic content and data (Policy)
- Description: Standardize evaluation, transparency reports, and watermarking/signatures embedded in velocity-field trajectories for provenance.
- Potential tools/workflows: Watermark injectors/detectors; model cards with solver/guidance specs; compliance dashboards.
- Assumptions/dependencies: Adoption by industry; robustness against removal; interoperable standards.
- Generative surrogates for PDE-constrained systems (Science/Engineering)
- Description: Use Fokker–Planck-informed transports as surrogate models for expensive simulators (fluid dynamics, material design).
- Potential tools/workflows: Operator-learning + diffusion hybrids; uncertainty-aware solvers; design-of-experiments loops.
- Assumptions/dependencies: Error bounds and reliability; domain trust; integration with existing simulation stacks.
- Energy grid digital twins with stochastic dynamics (Energy/Infrastructure)
- Description: Generative models that capture load, renewable variability, and contingencies for planning and resilience analysis.
- Potential tools/workflows: Scenario engines; guided risk simulations; operator dashboards.
- Assumptions/dependencies: High-fidelity data; stakeholder validation; alignment with regulatory and operational constraints.
- Interactive SDE/ODE simulators for education at scale (Academia/Education)
- Description: Widely adopted platforms that visualize generative trajectories, probability transport, and solver behavior for learning.
- Potential tools/workflows: Browser-based labs; curriculum integrations; automated grading on conceptual tasks.
- Assumptions/dependencies: Institutional adoption; sustained maintenance; accessible compute resources.
Glossary
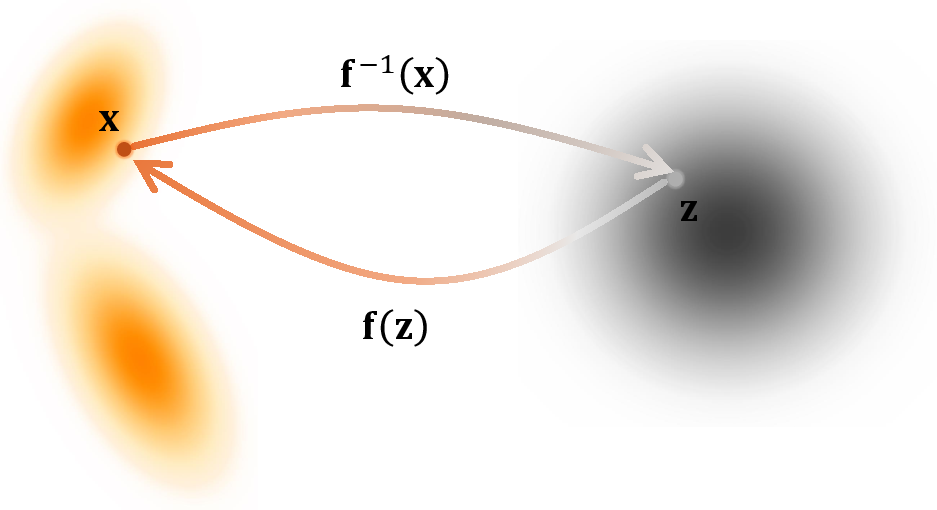
- Change-of-variables formula: A mathematical relation describing how probability densities transform under mappings, foundational to continuous-time generative flows. "The core insight behind diffusion models, despite their varied perspectives and origins, lies in the change-of-variables formula."
- Classifier guidance: A sampling technique that uses a classifier’s gradients or signals to steer generation toward desired attributes. "Techniques such as classifier guidance and classifier-free guidance make it possible to condition the generation process on user-defined objectives or attributes."
- Classifier-free guidance: A conditioning method that guides generation without an explicit classifier, typically by interpolating conditional and unconditional model outputs. "Techniques such as classifier guidance and classifier-free guidance make it possible to condition the generation process on user-defined objectives or attributes."
- Conditional Strategy: A modeling approach that turns the learning objective into a tractable regression by conditioning on time/noise. "Conditional Strategy"
- Continuity equation: A partial differential equation expressing conservation of probability mass over time under a flow. "explain their relations to the continuity equation and the Fokker--Planck perspective."
- Counting measures: A measure that assigns to a set the number of elements in it; integrals under counting measures reduce to sums. "All integrals are in the Lebesgue sense and reduce to sums under counting measures."
- Denoising Diffusion Probabilistic Models (DDPMs): A class of diffusion models trained via a variational objective to iteratively remove noise and generate data. "giving rise to Denoising Diffusion Probabilistic Models (DDPMs)~\citep{sohl2015deep,ho2020denoising}."
- Diffusion Probabilistic Models (DPM): Early discrete-time diffusion models that define a forward noising and learned reverse denoising process. "{Diffusion Probabilistic Models (DPM)}~\citep{sohl2015deep}"
- Distillation-Based Methods: Techniques that train a fast student generator to mimic a slow diffusion teacher, reducing sampling steps. "{Distillation-Based Methods} (\Cref{ch:distillation}): This approach focuses on training a student model to imitate the behavior of a pre-trained, slow diffusion model (the teacher)."
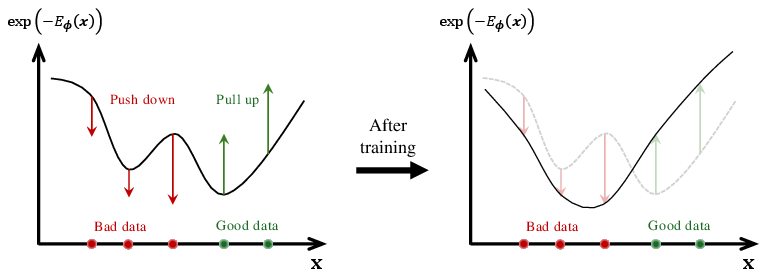
- Energy-Based Models (EBMs): Models that define an energy over configurations, with the log-density proportional to negative energy; underpin score-based diffusion. "{Energy-Based Model (EBM)}~\citep{ackley1985learning}"
- Entropy regularization: Adding an entropy term to optimization (e.g., optimal transport) to encourage smoother, stochastic solutions. "optimal transport with entropy regularization."
- f-divergences: A family of divergences between distributions defined by a convex function of the density ratio. "A broad family is the -divergences~\citep{csiszar1963informationstheoretische}:"
- Fisher divergence: A discrepancy between two distributions measured via the squared difference of their score functions. "The Fisher divergence is another important concept for (score-based) diffusion modeling (see \Cref{ch:score-based})."
- Flow map: The solution operator that maps states from one time to another along the trajectory of an ODE or SDE. "this approach learns the solution map (i.e., the flow map) directly from scratch"
- Flow Matching (FM): A framework that learns a velocity field so its induced flow transports a source distribution to a target. "{Flow Matching (FM)}~\citep{lipman2022flow}"
- Fokker–Planck equation: A PDE describing the time evolution of probability densities under stochastic dynamics. "extends to deeper concepts such as the Fokker--Planck equation and the continuity equation"
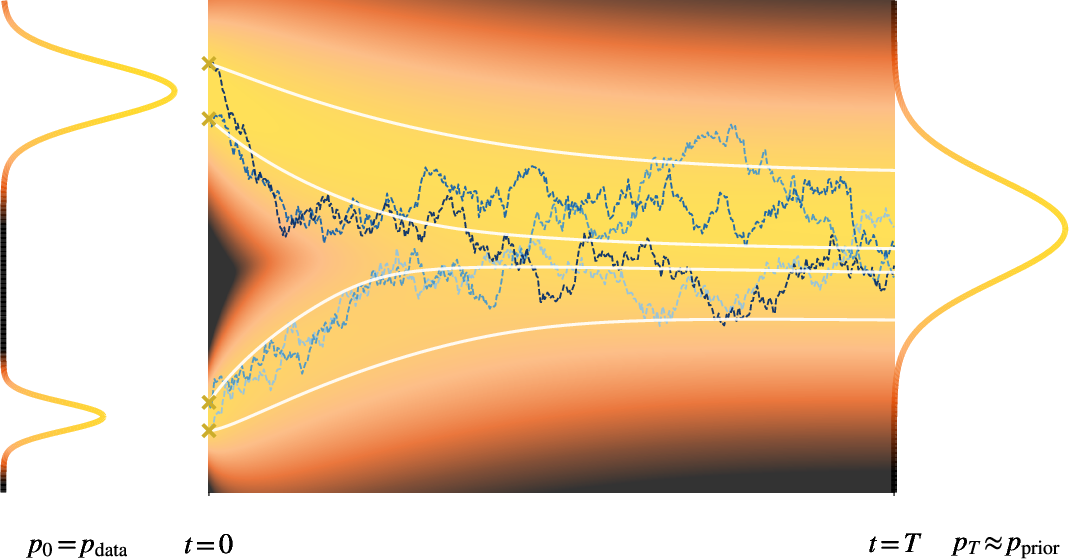
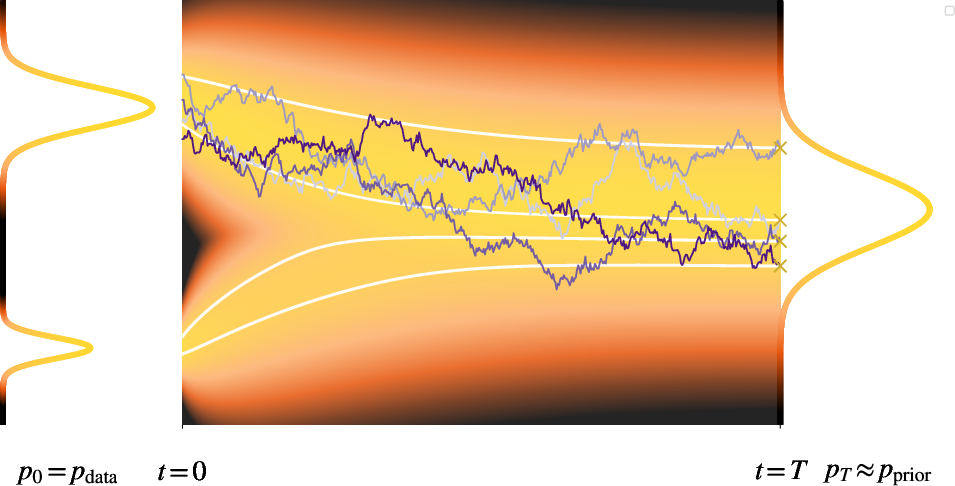
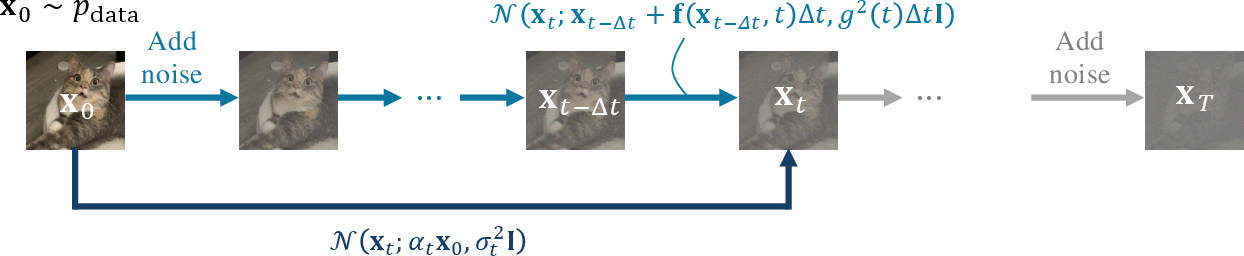
- Forward corruption process: The forward diffusion/noising process that gradually transforms data into noise. "Diffusion modeling begins by specifying a forward corruption process that gradually turns data into noise."
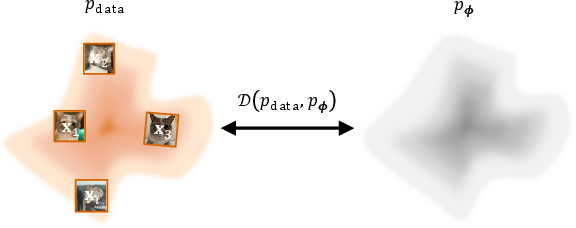
- Forward KL divergence: The Kullback–Leibler divergence measured as KL(p_data || p_model), encouraging mode covering. "A standard choice is the (forward) Kullback--Leibler divergence"
- Gaussian Flow Matching: A specific instantiation of flow matching using Gaussian structures/approximations. "Gaussian\Flow Matching"
- Girsanov's theorem: A result in stochastic calculus that relates measures of SDEs under changes of drift, key for reverse-time sampling. "Itô's formula and Girsanov's theorem"
- Itô's formula: A stochastic calculus rule for differentiating functions of stochastic processes, used to derive SDE properties. "Itô's formula and Girsanov's theorem"
- Jensen–Shannon divergence: A symmetric, smoothed divergence between distributions derived from KL to the mixture. "\quad\text{(Jensen--Shannon)}"
- Kullback–Leibler divergence: An asymmetric divergence measuring the expected log-density ratio; central to MLE and variational training. "A standard choice is the (forward) Kullback--Leibler divergence"
- Lebesgue sense: Refers to Lebesgue integration, the modern mathematical foundation for integrals over continuous spaces. "All integrals are in the Lebesgue sense"
- Marginal distribution: The distribution of a subset of variables (or at a given time) obtained by integrating out others. "ensuring that the marginal distribution at each time matches the marginal induced by a prescribed forward process"
- Maximum Likelihood Estimation (MLE): Parameter estimation by maximizing the likelihood (or log-likelihood) of observed data. "Forward KL and Maximum Likelihood Estimation (MLE)."
- Mode covering: A learning behavior where the model assigns probability across all data modes to avoid infinite forward KL. "Importantly, minimizing $\mathcal{D}_{\mathrm{KL}(p_{\mathrm{data} \| p_{\bm{\phi})$ encourages mode covering:"
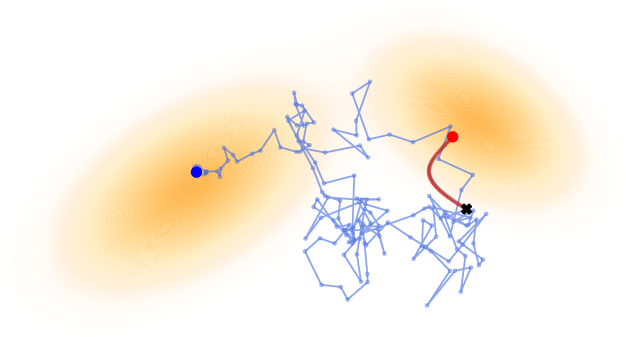
- Monte Carlo sampling: Randomized sampling methods used to draw approximate samples from a distribution. "using sampling methods such as Monte Carlo sampling from $p_{\bm{\phi}()$."
- Neural ODE (NODE): Models that parameterize continuous-time dynamics via neural networks to define flows over data. "{Neural ODE (NODE)}~\citep{chen2018neural}"
- Noise Conditional Score Network (NCSN): A model that learns the score function conditioned on noise level to enable denoising generation. "{Noise Conditional Score Network (NCSN)}~\citep{song2019generative}"
- Normalizing Flows: Invertible, differentiable transformations that map a simple base distribution to complex data distributions. "Normalizing Flows~\citep{rezende2015variational}"
- Numerical solvers: Algorithms for discretely integrating ODE/SDEs to accelerate sampling while preserving quality. "advanced numerical solvers that approximate the reverse process in fewer steps, reducing cost while preserving quality."
- Optimal transport: A theory of moving probability mass optimally from one distribution to another, often linked to Wasserstein distance. "connections to classical optimal transport and the Schrödinger bridge"
- Ordinary Differential Equation (ODE): A deterministic differential equation describing continuous-time evolution; used for generative flows. "its deterministic counterpart as an Ordinary Differential Equation (ODE)."
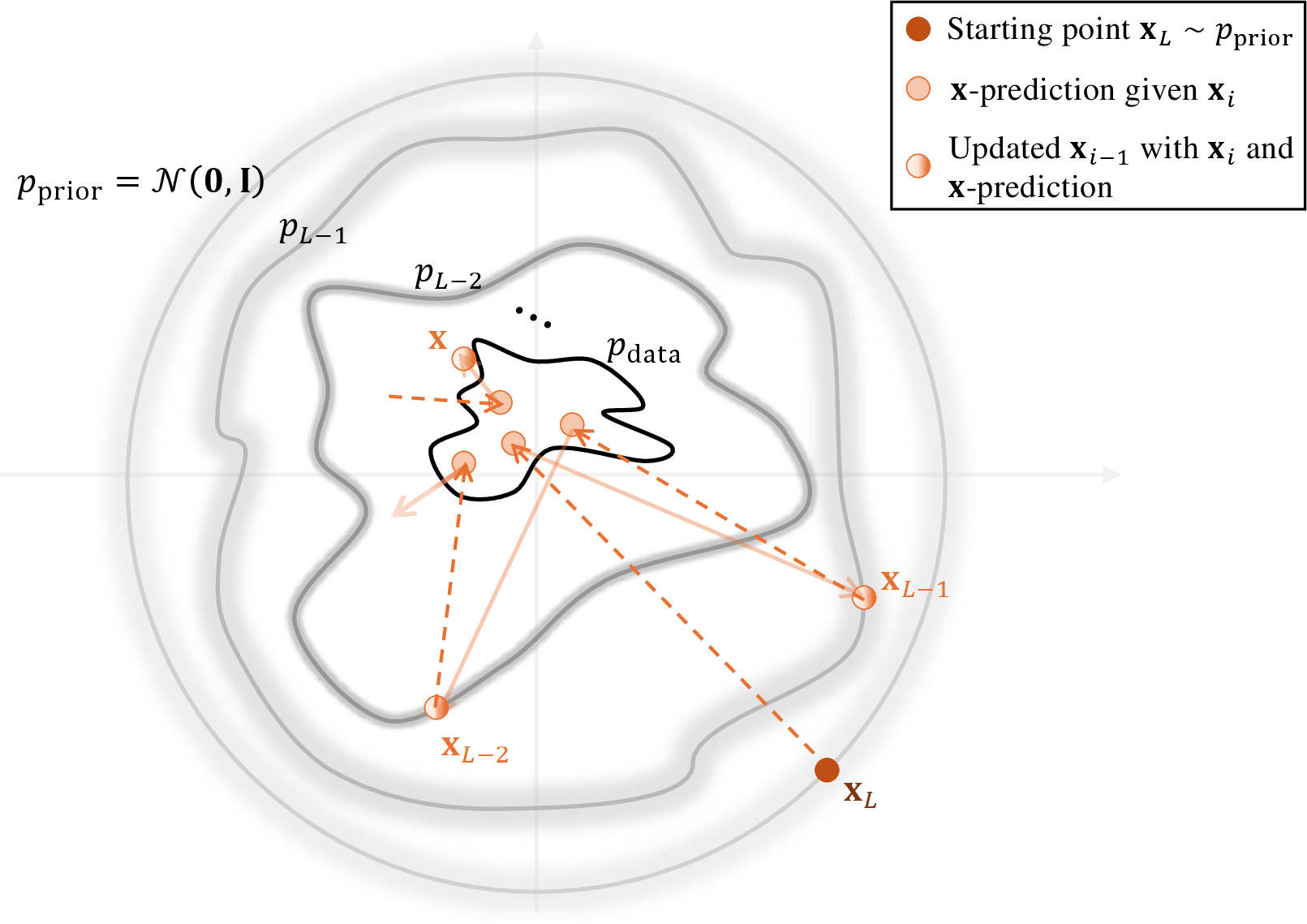
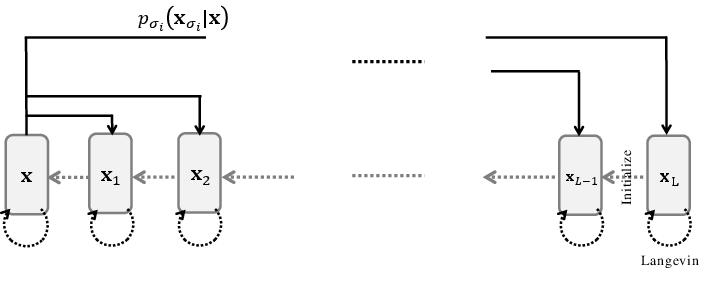
- Reverse-time process: The learned generative process that inverts the forward noising to transform noise back into data. "a reverse-time process approximated by a sequence of models performing gradual denoising:"
- Schrödinger bridge: A stochastic, entropy-regularized transport problem connecting distributions over time. "the Schrödinger bridge, interpreted as optimal transport with entropy regularization."
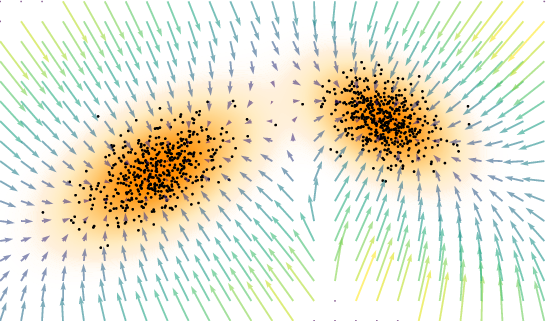
- Score function: The gradient of the log-density; indicates directions to higher probability and guides denoising. "It learns the score function, the gradient of the log data density"
- Score matching: A training method that fits a model’s score function to the data’s score, avoiding need for normalized densities. "it forms the basis of score matching (\Cref{eq:ebm-sm,eq:sm})"
- Score SDE: A continuous-time framework for score-based models that represents denoising via stochastic differential equations. "introduces the Score SDE framework"
- Stochastic Differential Equation (SDE): A differential equation with randomness, modeling noisy continuous-time dynamics in diffusion. "describes this denoising process as a Stochastic Differential Equation (SDE)"
- Variational Autoencoder (VAE): A generative model trained via a variational objective to encode/decode data; a precursor to DDPMs. "{Variational Autoencoder (VAE)}~\citep{kingma2013auto}"
- Variational objective: The optimization objective from variational inference used to train models like VAEs and DDPMs. "it frames diffusion as learning a denoising process through a variational objective"
- Velocity field: A time-dependent vector field whose flow transports the prior distribution to the data distribution. "The evolution is governed by a velocity field through an ODE"
- Wasserstein distance: An optimal transport metric measuring minimal cost to move probability mass between distributions. "the Wasserstein distance (see ."
Collections
Sign up for free to add this paper to one or more collections.