A Survey on Archetypal Analysis (2504.12392v1)

Abstract: Archetypal analysis (AA) was originally proposed in 1994 by Adele Cutler and Leo Breiman as a computational procedure to extract the distinct aspects called archetypes in observations with each observational record approximated as a mixture (i.e., convex combination) of these archetypes. AA thereby provides straightforward, interpretable, and explainable representations for feature extraction and dimensionality reduction, facilitating the understanding of the structure of high-dimensional data with wide applications throughout the sciences. However, AA also faces challenges, particularly as the associated optimization problem is non-convex. This survey provides researchers and data mining practitioners an overview of methodologies and opportunities that AA has to offer surveying the many applications of AA across disparate fields of science, as well as best practices for modeling data using AA and limitations. The survey concludes by explaining important future research directions concerning AA.

• The paper reviews archetypal analysis techniques that model data as convex mixtures, enabling interpretable feature extraction.
• It evaluates optimization methods like Frank-Wolfe and projected gradient to improve computational efficiency in non-convex settings.
• It discusses AA's applications in life sciences, physics, and computer science, and outlines current challenges and future research directions.

A Survey on Archetypal Analysis

Introduction

Archetypal Analysis (AA) is a method for extracting archetypes—idealized forms—from data by approximating observations as convex mixtures of these archetypes. Originally introduced by Cutler and Breiman in 1994, AA excels in providing explainable, interpretable representations which facilitate dimensionality reduction and feature extraction in high-dimensional datasets. This paper extensively reviews AA's methodologies, applications across disparate scientific domains, its algorithmic challenges due to non-convex optimization constraints, and future research directions.

Theoretical Background

The fundamental concept of AA involves modeling data as convex combinations of archetypes $\mathbf{A}$ defined within a convex hull of the dataset. This representation is achieved through the optimization of the Residual Sum of Squares (RSS), which is inherently non-convex. Several algorithmic strategies have arisen to approximate solutions, including alternating optimization, projected gradient methods, and manifold optimization approaches. Empirical results consistently demonstrate AA's ability to distill high-dimensional data to intuitively graspable extremes.

Figure 1: Bubble map with the main areas of AA applications.

Implementation Approaches

AA implementations entail optimization techniques such as the Frank-Wolfe algorithm, SMO procedures, and active-set methods for efficiently solving the associated convex quadratic programming problems within the simplex constraints. These methods provide computational stability across varied datasets such as images, spectra, and relational data. Additionally, initializations impact AA performance; strategies like FurthestSum and AA++ enhance convergence by effectively choosing starting archetypes far apart in data space.

Practical Applications

AA has been applied in life sciences for understanding evolutionary trade-offs and genetic diversity [shoval2012evolutionary] [gimbernat2022archetypal]. In physics, AA tackles spatiotemporal dynamics and chemical mixtures in spectroscopy [stone2002exploring] [morup2012archetypal]. In computer science, AA facilitates clustering, anomaly detection, and contributes robustly to recommendation systems and image recognition tasks [morup2010archetypal] [Xiong_2013_ICCV].

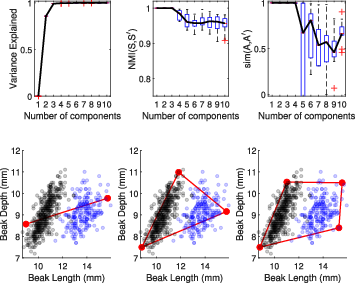
Figure 2: Analysis of data on Finches demonstrating the improvement from K=2 to K=3 for variance explanation and characterization of finch variability.

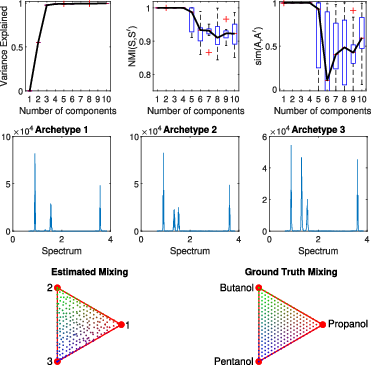
Figure 3: Analysis of NMR experiment flexibly characterizing chemical mixtures, showing optimal results at K=3.

Challenges and Future Directions

AA faces challenges in non-convex optimization and incomplete data handling. Future research aims to relax archetypal assumptions beyond convex combinations, enhance manifold learning integration, and derive automatic model order determinations. Continual advancements toward reliable estimation procedures and broadening kernel AA applications will deepen AA's impact on understanding complex datasets.

Conclusion

AA serves an essential role in dimensionality that interprets intricate datasets across diverse scientific realms. It furnishes avenues for interpretive data analysis and continues to inspire methods that unravel complexities inherent in our increasingly data-driven world. This survey underscores AA's versatility and opens pathways for progressing its foundational algorithms and applications in cutting-edge research explorations.