Task Generalization With AutoRegressive Compositional Structure: Can Learning From $D$ Tasks Generalize to $D^{T}$ Tasks? (2502.08991v2)

Abstract: LLMs exhibit remarkable task generalization, solving tasks they were never explicitly trained on with only a few demonstrations. This raises a fundamental question: When can learning from a small set of tasks generalize to a large task family? In this paper, we investigate task generalization through the lens of autoregressive compositional structure, where each task is a composition of $T$ operations, and each operation is among a finite family of $D$ subtasks. This yields a total class of size $D^T$. We first show that generalization to all $D^T$ tasks is theoretically achievable by training on only $\widetilde{O}(D)$ tasks. Empirically, we demonstrate that Transformers achieve such exponential task generalization on sparse parity functions via In-context Learning (ICL) and chain-of-thought (CoT) reasoning. We further show generalization in arithmetic and translation, beyond parity functions.

• The paper introduces a theoretical framework showing that ARC structure reduces the sample complexity from exponential to polynomial with only O(D log D) training tasks.
• It empirically validates the model on parity, arithmetic, and multi-step language translation tasks, demonstrating near-perfect generalization using Chain-of-Thought reasoning.
• The study highlights the critical role of diverse task selection and sufficient context length for robust generalization in autoregressive Transformer architectures.

Task Generalization with AutoRegressive Compositional Structure: Quantitative and Empirical Analysis

Introduction

This paper presents a rigorous theoretical and empirical investigation into the phenomenon of task generalization in LLMs, focusing on the role of AutoRegressive Compositional (ARC) structure. The central question addressed is: Can a model trained on $D$ tasks generalize to an exponentially larger family of $D^T$ tasks? The authors formalize ARC structure, derive sample complexity bounds for task generalization, and validate these results with experiments on parity functions, arithmetic, and multi-step language translation. The work provides a quantitative framework for understanding how compositionality enables efficient generalization in autoregressive models, particularly Transformers.

Theoretical Framework: AutoRegressive Compositional Structure

The ARC structure is defined as a function class where each task is a composition of $T$ operations, each selected from a finite set of $D$ subtasks. Formally, the output sequence $\bm{y} = (y_1, \dots, y_T)$ is generated autoregressively, with each $y_t$ sampled from a conditional distribution $P_{\theta_t}(y_t \mid \bm{x}, \bm{y}_{<t})$. The total number of possible tasks is $D^T$, reflecting exponential growth in $T$.

The main theoretical result establishes that, under mild identifiability assumptions, a learner can generalize to all $D^T$ tasks by training on only $\tilde{O}(D)$ tasks (up to logarithmic factors). The proof leverages maximum likelihood estimation and total variation-based discrimination, showing that compositional structure fundamentally reduces sample complexity from exponential to polynomial in $D$.

Parity Functions: Chain-of-Thought Enables Exponential Generalization

The sparse parity problem serves as a canonical example. Without Chain-of-Thought (CoT) reasoning, the parity function class is $ARC(\binom{d}{k}, 1)$, requiring $O(d^k)$ training tasks for generalization. With CoT, the problem is decomposed into $k$ steps, each with $d$ choices, yielding $ARC(d, k)$ and reducing the required number of training tasks to $O(d \log d)$.

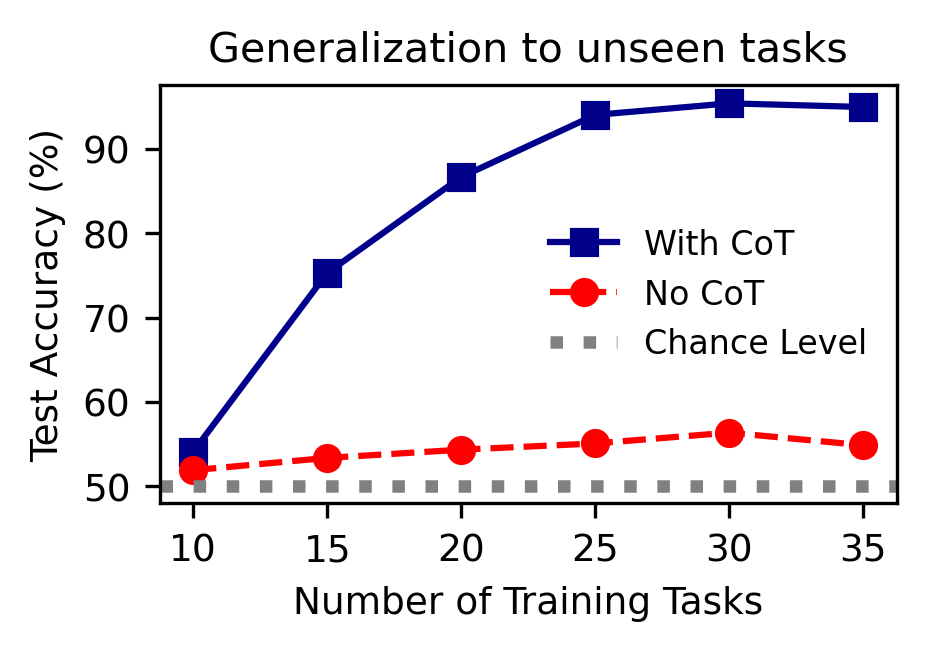
Figure 1: We train a Transformer to learn parity functions through In-Context Learning (ICL): given a demonstration sequence $$(\bm x_1, f(\bm x_1)), \dots, (\bm x_n, f(\bm x_n))$$, infer the target $f(\bm x_{\mathrm{query}})$ for a new input.

Empirically, Transformers trained with CoT achieve near-perfect generalization to unseen parity tasks with only $O(d \log d)$ training tasks, matching theoretical predictions. In contrast, standard ICL without CoT fails to generalize, even in-distribution.

Figure 2: Chain-of-Thought (CoT) reasoning enables generalization in parity tasks, while standard ICL fails.

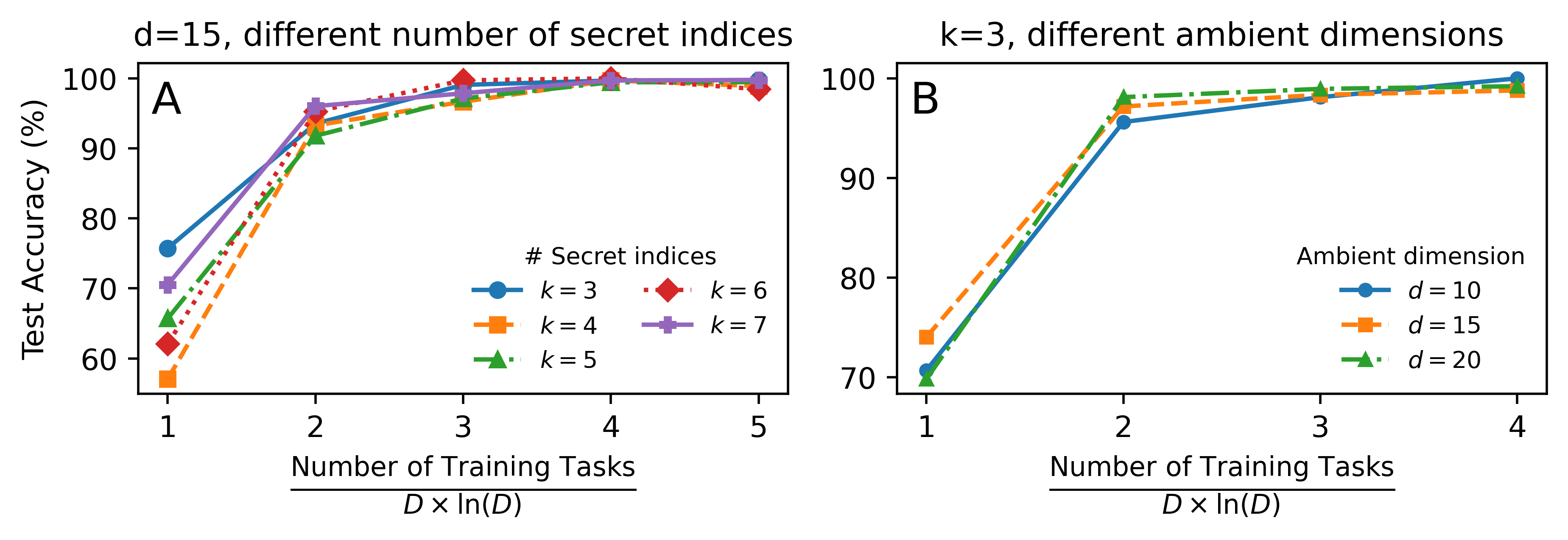
Figure 3: Test accuracy on unseen tasks. For parity: $D = d$ (ambient dimension), $T = k$ (number of secret indices). Empirical scaling closely follows theoretical $D \ln(D)$.

Empirical Scaling Laws: Parity, Arithmetic, and Language Translation

The authors conduct extensive experiments to validate the theoretical scaling laws. For parity functions, increasing $T$ (number of secret indices) or $D$ (ambient dimension) does not increase the number of training tasks required for generalization, as long as $O(D \log D)$ tasks are used. Linear probing of Transformer hidden states confirms that the model identifies and executes subtasks at each CoT step.

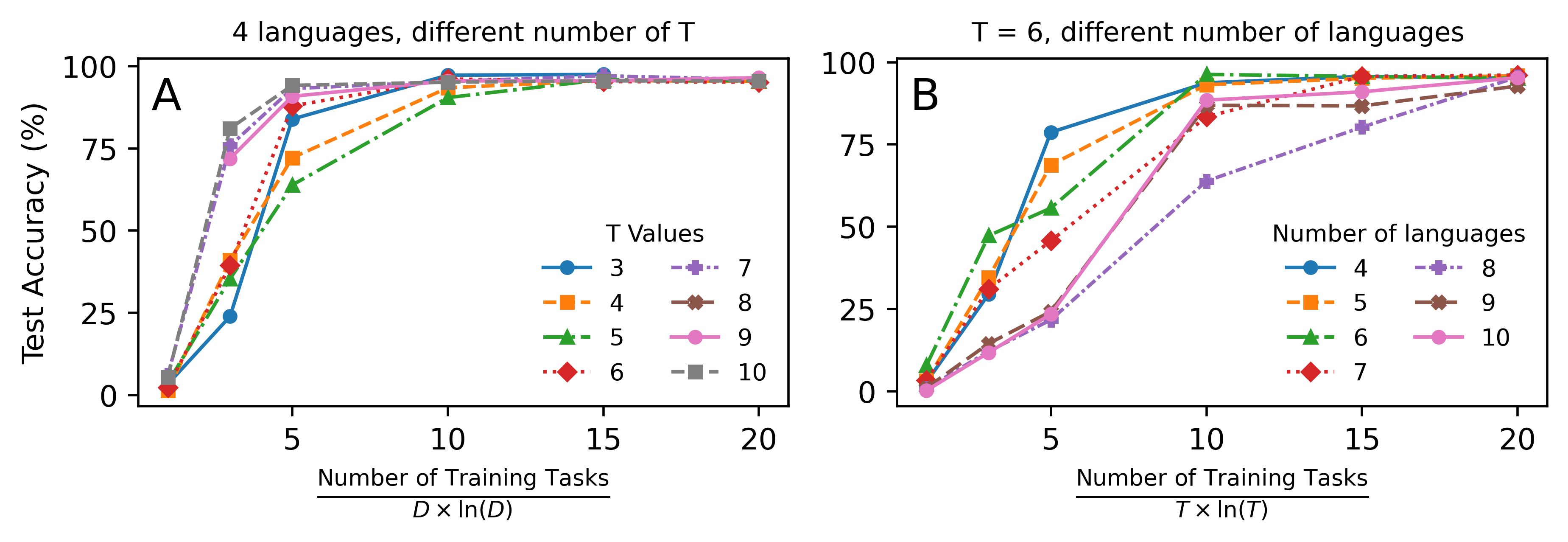
Figure 4: Task generalization for language translation task: $D$ is the number of languages and $T$ is the length of steps.

For arithmetic tasks, the ARC structure is $ARC(2, d-1)$, and empirical results show that training on a few hundred tasks enables generalization to millions of unseen tasks. In multi-step language translation, the ARC structure arises naturally, and the empirical scaling matches $O(D \ln D T)$ for $D$-scaling, with a linear dependency on $T$ due to error accumulation.

Task Selection and Adversarial Sampling

The paper highlights that i.i.d. sampling of training tasks is crucial for robust generalization. Adversarial selection, such as excluding specific positional configurations, can cause generalization to fail even when the training set is exponentially large. This underscores the importance of diversity in training task selection for compositional generalization.

Context Length and In-Distribution Generalization

Additional experiments show that sufficient context length is necessary for strong performance. Transformers with ICL and no CoT fail to generalize even in-distribution as the number of tasks increases, reinforcing the necessity of compositional reasoning for efficient generalization.

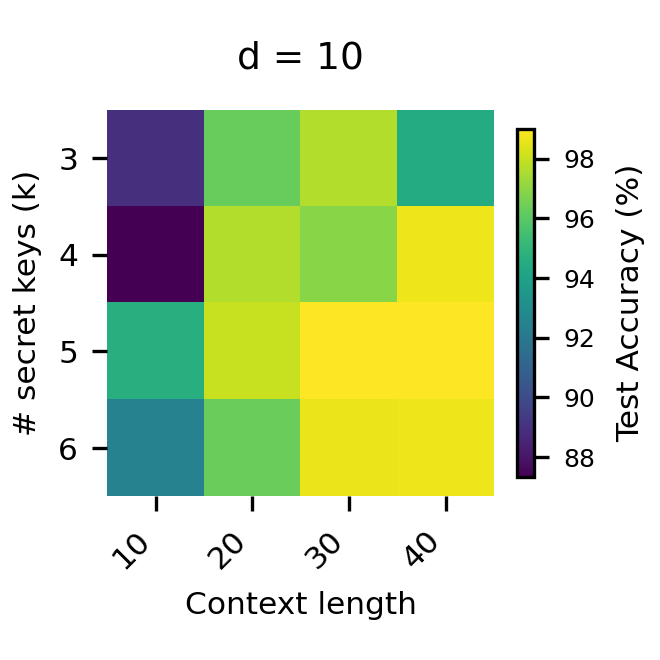
Figure 5: The effect of context length on performance.

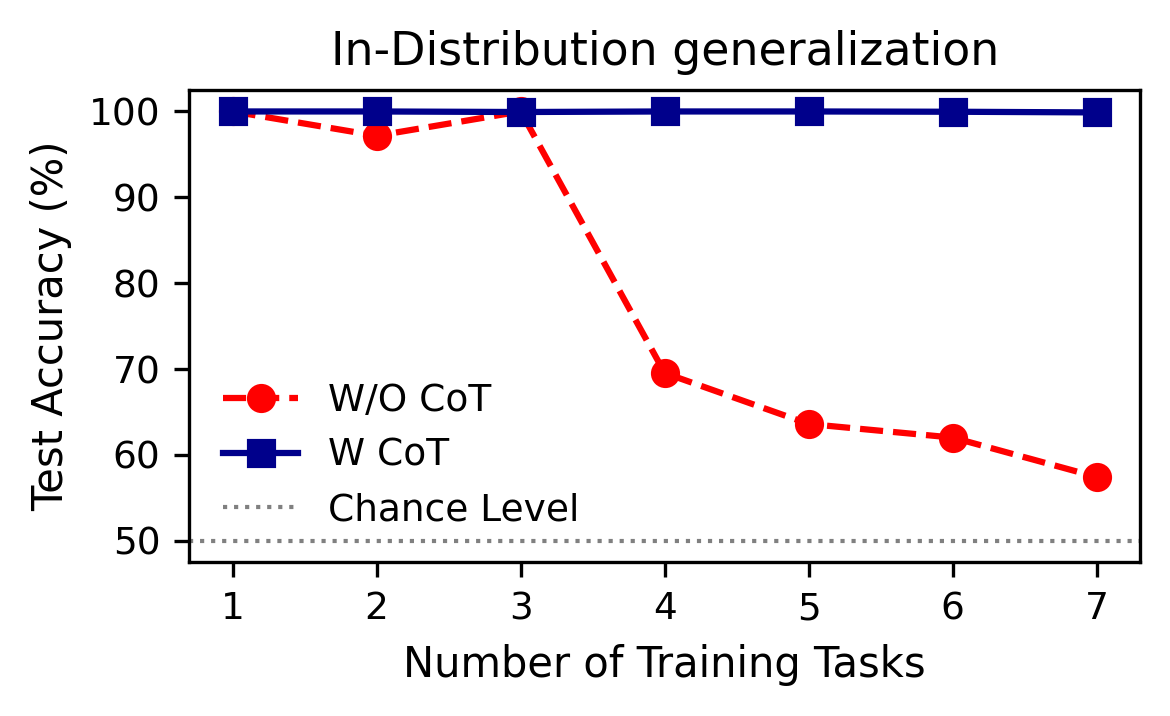
Figure 6: ICL without CoT even fails to generalize in distribution.

Implementation and Practical Considerations

The empirical results are obtained using standard Transformer architectures (e.g., GPT-2), trained from scratch with cross-entropy loss on next-token prediction. CoT is implemented by decomposing outputs into intermediate reasoning steps, and linear probes are used to analyze hidden representations. The experiments demonstrate that ARC structure and CoT can be leveraged in practice to achieve exponential task generalization with modest computational resources.

Implications and Future Directions

The findings have significant implications for the design and training of autoregressive models. By exploiting compositional structure and CoT reasoning, models can generalize efficiently to vast task families, reducing the need for exhaustive task-specific supervision. This framework provides a principled approach to understanding and engineering generalization in LLMs, with potential applications in program synthesis, mathematical reasoning, and decision-making.

Future research should explore the extension of these principles to more complex real-world tasks, investigate the limits of compositional generalization under various architectural and data constraints, and develop methods for automated discovery of compositional structure in unstructured domains.

Conclusion

This work establishes a quantitative theory of task generalization under ARC structure, demonstrating both theoretically and empirically that exponential generalization to $D^T$ tasks is achievable with only $\tilde{O}(D)$ training tasks. The results highlight the power of compositionality and CoT reasoning in enabling efficient generalization in autoregressive models, providing a foundation for future advances in structured learning and generalization in AI.