Papers
Topics
Authors
Recent
Search
2000 character limit reached

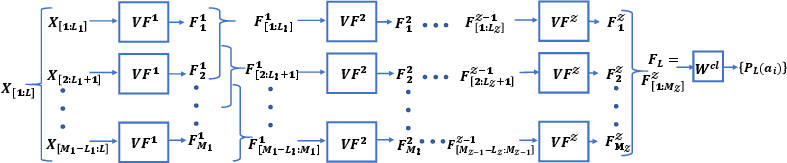
Volterra Neural Networks (VNNs)

Published 21 Oct 2019 in cs.CV, cs.LG, and eess.IV | (1910.09616v5)

Abstract: The importance of inference in Machine Learning (ML) has led to an explosive number of different proposals in ML, and particularly in Deep Learning. In an attempt to reduce the complexity of Convolutional Neural Networks, we propose a Volterra filter-inspired Network architecture. This architecture introduces controlled non-linearities in the form of interactions between the delayed input samples of data. We propose a cascaded implementation of Volterra Filtering so as to significantly reduce the number of parameters required to carry out the same classification task as that of a conventional Neural Network. We demonstrate an efficient parallel implementation of this Volterra Neural Network (VNN), along with its remarkable performance while retaining a relatively simpler and potentially more tractable structure. Furthermore, we show a rather sophisticated adaptation of this network to nonlinearly fuse the RGB (spatial) information and the Optical Flow (temporal) information of a video sequence for action recognition. The proposed approach is evaluated on UCF-101 and HMDB-51 datasets for action recognition, and is shown to outperform state of the art CNN approaches.

Definition Search Book Streamline Icon: https://streamlinehq.com
References (48)
  1. Tensorflow: A system for large-scale machine learning. In 12th {normal-{\{{USENIX}normal-}\}} Symposium on Operating Systems Design and Implementation ({normal-{\{{OSDI}normal-}\}} 16), pages 265–283, 2016.
  2. Sequential deep learning for human action recognition. In International workshop on human behavior understanding, pages 29–39. Springer, 2011.
  3. Benign overfitting in linear regression. arXiv preprint arXiv:1906.11300, 2019.
  4. Quo vadis, action recognition? a new model and the kinetics dataset. In proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 6299–6308, 2017.
  5. Histograms of oriented gradients for human detection. 2005.
  6. Imagenet: A large-scale hierarchical image database. In 2009 IEEE conference on computer vision and pattern recognition, pages 248–255. Ieee, 2009.
  7. Temporal 3d convnets: New architecture and transfer learning for video classification. arXiv preprint arXiv:1711.08200, 2017a.
  8. Deep temporal linear encoding networks. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 2329–2338, 2017b.
  9. Learning hierarchical features for scene labeling. IEEE transactions on pattern analysis and machine intelligence, 35(8):1915–1929, 2012.
  10. Convolutional two-stream network fusion for video action recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1933–1941, 2016.
  11. Slowfast networks for video recognition. In Proceedings of the IEEE/CVF international conference on computer vision, pages 6202–6211, 2019.
  12. William J Firey. Remainder formulae in taylor’s theorem. The American Mathematical Monthly, 67(9):903–905, 1960.
  13. Compact bilinear pooling. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 317–326, 2016.
  14. Generative adversarial nets. In Advances in neural information processing systems, pages 2672–2680, 2014.
  15. Improved training of wasserstein gans. In Advances in neural information processing systems, pages 5767–5777, 2017.
  16. Learning with side information through modality hallucination. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 826–834, 2016.
  17. Image-to-image translation with conditional adversarial networks. In Proceedings of the IEEE conference on computer vision and pattern recognition, pages 1125–1134, 2017.
  18. 3d convolutional neural networks for human action recognition. IEEE transactions on pattern analysis and machine intelligence, 35(1):221–231, 2012.
  19. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 1725–1732, 2014.
  20. The kinetics human action video dataset. arXiv preprint arXiv:1705.06950, 2017.
  21. Yu Kong and Yun Fu. Human action recognition and prediction: A survey. arXiv preprint arXiv:1806.11230, 2018.
  22. On stabilizing generative adversarial networks (stgans).
  23. Imagenet classification with deep convolutional neural networks. In Advances in neural information processing systems, pages 1097–1105, 2012.
  24. Hmdb: a large video database for human motion recognition. In 2011 International Conference on Computer Vision, pages 2556–2563. IEEE, 2011.
  25. Trainable convolution filters and their application to face recognition. IEEE transactions on pattern analysis and machine intelligence, 34(7):1423–1436, 2011.
  26. Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11):2278–2324, 1998.
  27. Bilinear cnns for fine-grained visual recognition. arXiv preprint arXiv:1504.07889, 2015.
  28. Recognizing realistic actions from videos in the wild. Citeseer, 2009.
  29. Sparse generative adversarial network. In Proceedings of the IEEE International Conference on Computer Vision Workshops, pages 0–0, 2019.
  30. Modeling temporal structure of decomposable motion segments for activity classification. In European conference on computer vision, pages 392–405. Springer, 2010.
  31. Multilayer neural network structure as volterra filter. In Proceedings of IEEE International Symposium on Circuits and Systems-ISCAS’94, volume 6, pages 253–256. IEEE, 1994.
  32. Decision level fusion: An event driven approach. In 2018 26th European Signal Processing Conference (EUSIPCO), pages 2598–2602. IEEE, 2018a.
  33. Cross-modality distillation: A case for conditional generative adversarial networks. In 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pages 2926–2930. IEEE, 2018b.
  34. Event driven fusion. arXiv preprint arXiv:1904.11520, 2019.
  35. Walter Rudin et al. Principles of mathematical analysis, volume 3. McGraw-hill New York, 1964.
  36. Martin Schetzen. The volterra and wiener theories of nonlinear systems. 1980.
  37. Overfeat: Integrated recognition, localization and detection using convolutional networks. arXiv preprint arXiv:1312.6229, 2013.
  38. Two-stream convolutional networks for action recognition in videos. In Advances in neural information processing systems, pages 568–576, 2014.
  39. Video google: A text retrieval approach to object matching in videos. In null, page 1470. IEEE, 2003.
  40. Ucf101: A dataset of 101 human actions classes from videos in the wild. arXiv preprint arXiv:1212.0402, 2012.
  41. Marshall H Stone. The generalized weierstrass approximation theorem. Mathematics Magazine, 21(5):237–254, 1948.
  42. Learning spatiotemporal features with 3d convolutional networks. In Proceedings of the IEEE international conference on computer vision, pages 4489–4497, 2015.
  43. A closer look at spatiotemporal convolutions for action recognition. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, pages 6450–6459, 2018.
  44. Vito Volterra. Theory of functionals and of integral and integro-differential equations. Courier Corporation, 2005.
  45. Evaluation of local spatio-temporal features for action recognition. 2009.
  46. Human activity modeling as brownian motion on shape manifold. In International Conference on Scale Space and Variational Methods in Computer Vision, pages 628–639. Springer, 2011.
  47. A duality based approach for realtime tv-l 1 optical flow. In Joint pattern recognition symposium, pages 214–223. Springer, 2007.
  48. Non-linear convolution filters for cnn-based learning. In Proceedings of the IEEE International Conference on Computer Vision, pages 4761–4769, 2017.
Citations (9)
View on Semantic Scholar

Summary

  • The paper demonstrates how VNNs leverage Volterra series to introduce controlled non-linearities, achieving enhanced performance in action recognition and image generation.
  • It details a nested and overlapping filter architecture that optimizes parameter efficiency and reduces computational complexity compared to CNNs and LSTMs.
  • The study validates VNNs' robustness to noise and frame rate variations while showcasing versatility in applications including GAN-based image generation.

Volterra Neural Networks (VNNs): Technical Overview

Volterra Neural Networks (VNNs) introduce a novel approach to neural network architectures inspired by Volterra series and filters, aiming to tackle the complexity and computational challenges inherent in Convolutional Neural Networks (CNNs). This essay provides an expert analysis of the VNN framework, exploring its design, implementation, and performance in action recognition and image generation tasks.

Volterra Filter-based Architecture

Theoretical Basis: Volterra Series

The Volterra series serves as a foundational mathematical tool for modeling non-linear systems, representing systems using a series of integrals. In the context of VNNs, the series introduces controlled non-linearities through interactions between delayed data samples. The architecture leverages these principles to implement a Volterra-filter-inspired network, with the filters structured in cascades to explore higher-order terms without excessive parameterization. Figure 1

Figure 1: Adaptive Volterra Filter.

Nested and Overlapping Volterra Filters

The nested Volterra filter architecture allows a structured layered approach reminiscent of CNNs but significantly optimizes parameter efficiency. The overlapping Volterra Neural Network (O-VNN) implementation provides a detailed block diagram that elucidates how cascaded filters manage high-order interactions. Figure 2

Figure 3: Block diagram for an Overlapping Volterra Neural Network.

Comparison with Conventional Methods

Relation to CNNs and LSTMs

While CNNs introduce non-linearities via activation functions, VNNs achieve this through higher-order Volterra terms, resulting in potentially more fine-grained learning. The comparison extends to the capabilities of VNNs versus Long-Short Term Memory networks (LSTMs), where VNNs inherently model temporal dynamics without the explicit use of activations, hence learning approximations of activation functions inherently.

Computational Efficiency

A key advantage of the VNN architecture is the substantial reduction in computational complexity compared to traditional CNN models. This efficiency is critical when considering deployment on resource-constrained devices, where VNNs maintain remarkable performance with fewer parameters, as shown in various datasets like UCF-101 and HMDB-51.

Practical Implications and Performance

Action Recognition

The VNN model demonstrated competitive performance across standard action recognition datasets. Notably, the implementation outperformed state-of-the-art models when trained from scratch, emphasizing its potential for tasks with limited training data. The non-linear fusion of spatial and temporal information streams further supports improved accuracy, revealing intrinsic relationships between different data modalities. Figure 4

Figure 5: (a) Input Video, (b) Features extracted by only RGB stream, (c) Features extracted by Two-Stream Volterra Filtering.

Robustness to Noise and Frame Rate Variations

VNNs exhibit enhanced robustness to Gaussian noise and variations in frame rates, highlighting their capability to generalize better under sub-optimal conditions, where traditional CNNs might falter. Figure 6

Figure 2: Performance comparison between VNN and CNN implementations when noise is added to the input videos.

Image Generation with GANs

The VNN framework's adaptability extends to generative models like GANs, where it contributes to generating high-quality images using datasets such as CIFAR-10. This application further underscores the versatility of Volterra-based architectures in addressing diverse AI challenges. Figure 7

Figure 7

Figure 7

Figure 8: Generated images using Cifar10 Dataset.

Conclusion

Volterra Neural Networks offer a promising alternative to conventional deep learning architectures, particularly excelling in tasks demanding efficient computation and robust modeling capabilities. By harnessing the nuanced capabilities of Volterra series, VNNs deliver enhanced performance in video action recognition and generative tasks, paving the way for future developments in AI systems that combine reduced complexity with high accuracy. Further exploration and optimization of VNNs could lead to broader adoption in varying domains where traditional models remain impractical.

File Document Download Save Streamline Icon: https://streamlinehq.com Markdown

Paper to Video (Beta)

Whiteboard

No one has generated a whiteboard explanation for this paper yet.

Ai Sparkles Streamline Icon: https://streamlinehq.com Sign Up to Generate

Open Problems

We haven't generated a list of open problems mentioned in this paper yet.

Ai Sparkles Streamline Icon: https://streamlinehq.com Generate Now

Authors (2)

  1. Siddharth Roheda 
  2. Hamid Krim 

Collections

Sign up for free to add this paper to one or more collections.

User Circle Single Streamline Icon: https://streamlinehq.com Sign Up