Accuracy, Memory Efficiency and Generalization: A Comparative Study on Liquid Neural Networks and Recurrent Neural Networks (2510.07578v1)

Abstract: This review aims to conduct a comparative analysis of liquid neural networks (LNNs) and traditional recurrent neural networks (RNNs) and their variants, such as long short-term memory networks (LSTMs) and gated recurrent units (GRUs). The core dimensions of the analysis include model accuracy, memory efficiency, and generalization ability. By systematically reviewing existing research, this paper explores the basic principles, mathematical models, key characteristics, and inherent challenges of these neural network architectures in processing sequential data. Research findings reveal that LNN, as an emerging, biologically inspired, continuous-time dynamic neural network, demonstrates significant potential in handling noisy, non-stationary data, and achieving out-of-distribution (OOD) generalization. Additionally, some LNN variants outperform traditional RNN in terms of parameter efficiency and computational speed. However, RNN remains a cornerstone in sequence modeling due to its mature ecosystem and successful applications across various tasks. This review identifies the commonalities and differences between LNNs and RNNs, summarizes their respective shortcomings and challenges, and points out valuable directions for future research, particularly emphasizing the importance of improving the scalability of LNNs to promote their application in broader and more complex scenarios.

• The paper demonstrates that Liquid Neural Networks, leveraging continuous-time dynamics, can outperform traditional RNNs in accuracy and generalization.
• It details a comparative methodology using closed-form models and case studies, highlighting reduced parameters and faster inference in LNNs.
• The study implies enhanced adaptability to non-stationary data and energy-efficient performance, promising for edge-device implementations.

Introduction

The paper "Accuracy, Memory Efficiency and Generalization: A Comparative Study on Liquid Neural Networks and Recurrent Neural Networks" (2510.07578) presents a comprehensive analysis comparing Liquid Neural Networks (LNNs) with traditional Recurrent Neural Networks (RNNs). It focuses on model accuracy, memory efficiency, and generalization abilities. LNNs, inspired by biological neural systems and continuous-time dynamics, offer significant advantages in handling non-stationary data and demonstrating superior out-of-distribution (OOD) generalization. On the other hand, RNNs, with their mature ecosystem, are foundational in sequence modeling despite known limitations.

Model Architecture

Recurrent Neural Networks (RNNs)

RNNs, including their variants LSTMs and GRUs, process temporal dependencies via discrete time steps and gating mechanisms. RNNs struggle with challenges like gradient vanishing/explosion and computational inefficiencies for long sequences. LSTMs solve some of the gradient issues by using explicit gating mechanisms; however, they remain parameter-heavy and face inherent efficiency limitations.

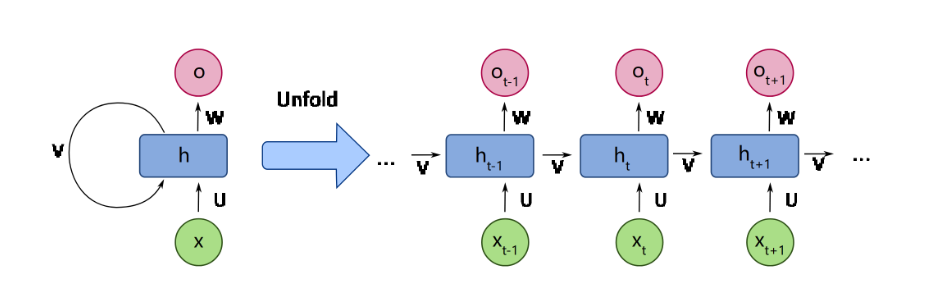
Figure 1: Recurrent Neural Network (RNN) unfolding representation illustrating the temporal expansion of recurrent connections. Each time step updates hidden state $h_t$, and produces output $o_t$ with shared weight matrices.

Liquid Neural Networks (LNNs)

LNNs implement continuous-time dynamics through ordinary differential equations (ODEs), offering inherently adaptive temporal mechanisms. This allows them to handle irregular data sampling and achieve stronger generalization capabilities. Key LNN architectures include Liquid Time-Constant networks (LTCs), Closed-form Continuous-time (CfC) networks, and Neural Circuit Policies (NCPs).

Figure 2: Conceptual architecture of a Liquid Neural Network (LNN), comprising input, liquid, and readout layers.

Comparative Analysis

Accuracy

LNNs have shown superior or equivalent accuracy compared to traditional RNNs across various benchmark tasks. Their continuous dynamics and adaptive time constants confer advantages in dynamic or noisy environments. CfC models leverage closed-form solutions for fast training and inference, achieving high accuracy on tasks like ICU patient trajectory prediction.

Memory Efficiency

Liquid Neural Networks demonstrate parameter efficiency without compromising performance. NCPs and CfC models highlight reduced parameter counts compared to LSTM and GRU, which are advantageous for low-resource environments and edge-device implementations.

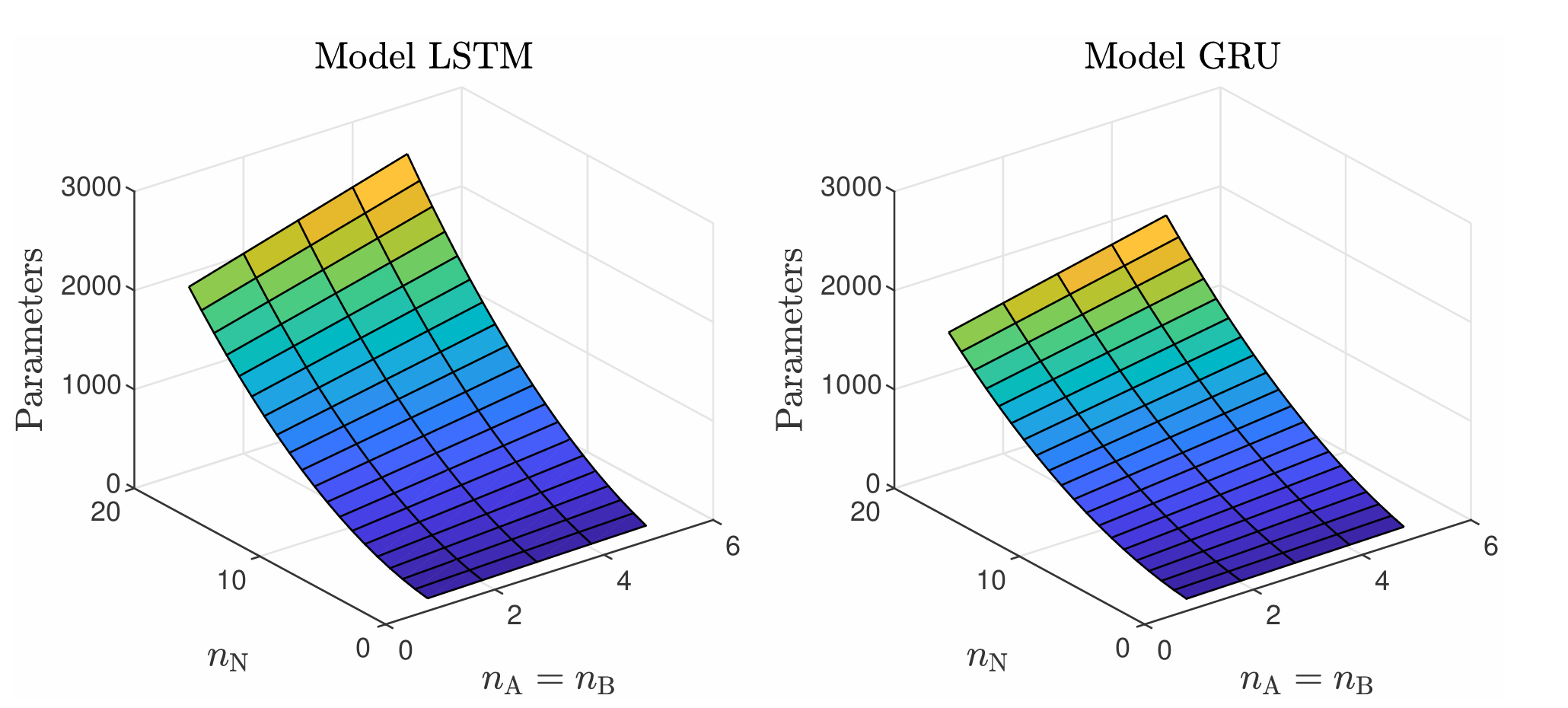
Figure 3: The number of the parameters of the Long Short-Term Memory (LSTM) and Gated Recurrent Unit (GRU) models as a function of the number of neurons.

Computational Efficiency

Despite being computationally intensive due to solver dependencies, LNNs, particularly CfC and NCP, offer efficiency gains such as reduced inference latency and energy usage on neuromorphic hardware. This contrasts with the sequential processing costs inherent in RNNs.

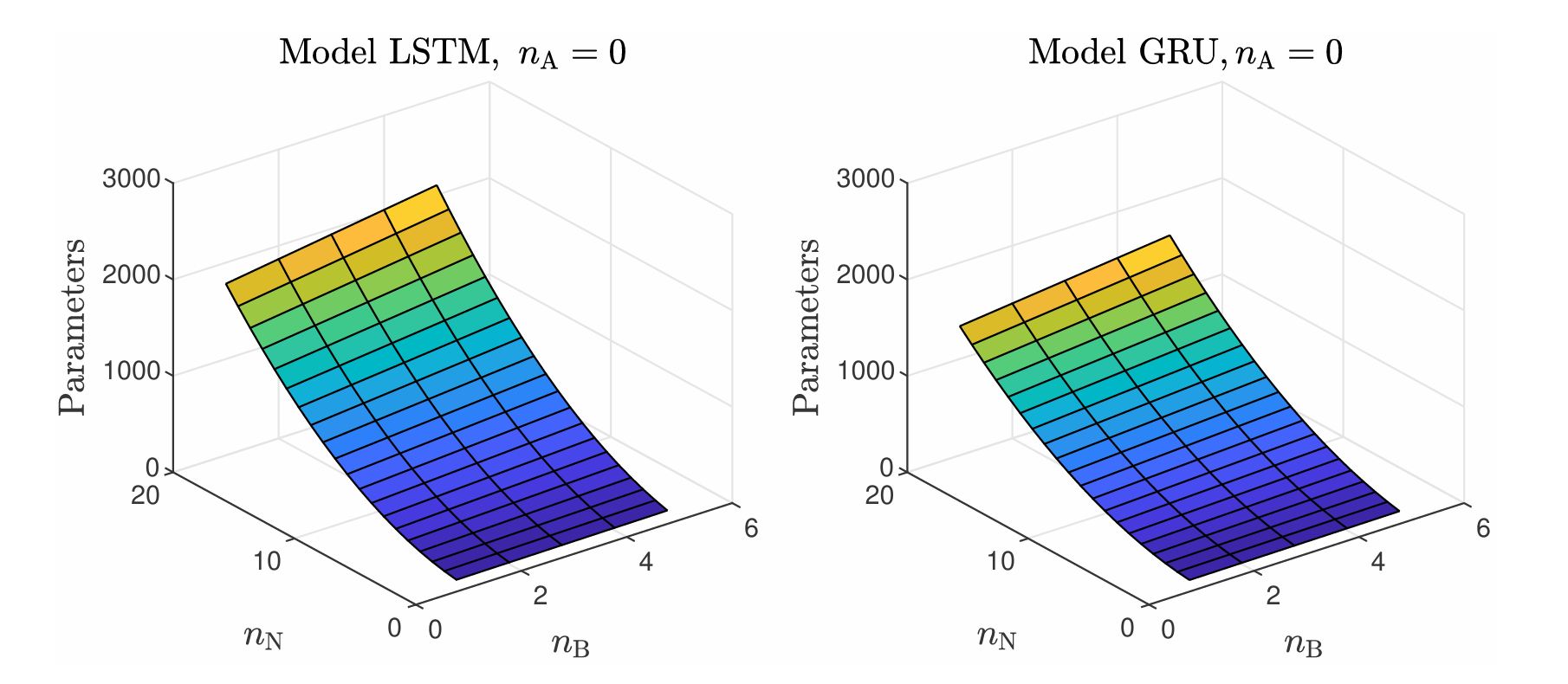
Figure 4: The number of parameters of the LSTM and GRU models as a function of neuron count.

Generalization Ability

LNNs demonstrate robust noise resistance and superior OOD generalization capabilities, crucial for real-world applications subject to distribution shifts. This results from continuous-time processing enabling adaptive responses to dynamic data characteristics.

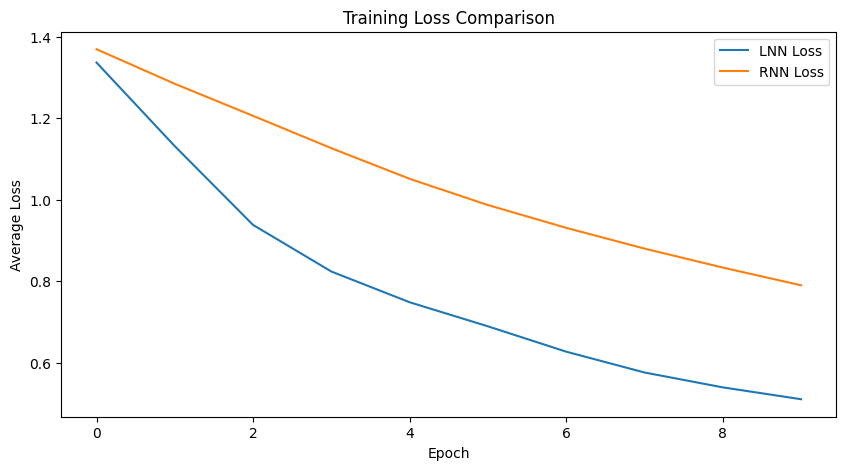
Figure 5: Training loss comparison.

Case Studies

Trajectory and Time-Series Prediction

The case studies using Walker2d trajectories and damped sine waves illustrate LNNs' capacity to model complex dynamics with fewer parameters and sophisticated efficiency. In these settings, LNNs consistently exhibited robust learning characteristics under noisy conditions.

Figure 6: True values and Liquid Time-Constant (LTC) prediction results for Walker2d trajectory.

ICU Patient Health Prediction

The CfC model utilized in ICU patient trajectory prediction showcases substantial gains in memory efficiency and robust long-horizon predictions over GRU, facilitating improved parameter efficiency and reduced computational overhead.

Figure 7: Prediction error comparison (RMSE and MAE) between CfC and GRU on ICU patient trajectories.

Future Work and Challenges

The paper identifies avenues such as scaling LNNs for large data sets and adapting them for energy-efficient hardware. Enhancing robustness in dynamic environments and exploring hybrid architectures integrating LNN dynamics with complementary inductive biases are promising directions.

Conclusion

LNNs offer compelling advantages in handling continuous data dynamics, adaptability, and efficient learning mechanisms. As neural architectures evolve, LNNs present strong potential for tackling limitations inherent in traditional RNNs, particularly in environments demanding robust, efficient, and adaptive models. Their integration into bigger systems may drive future AI advancements.