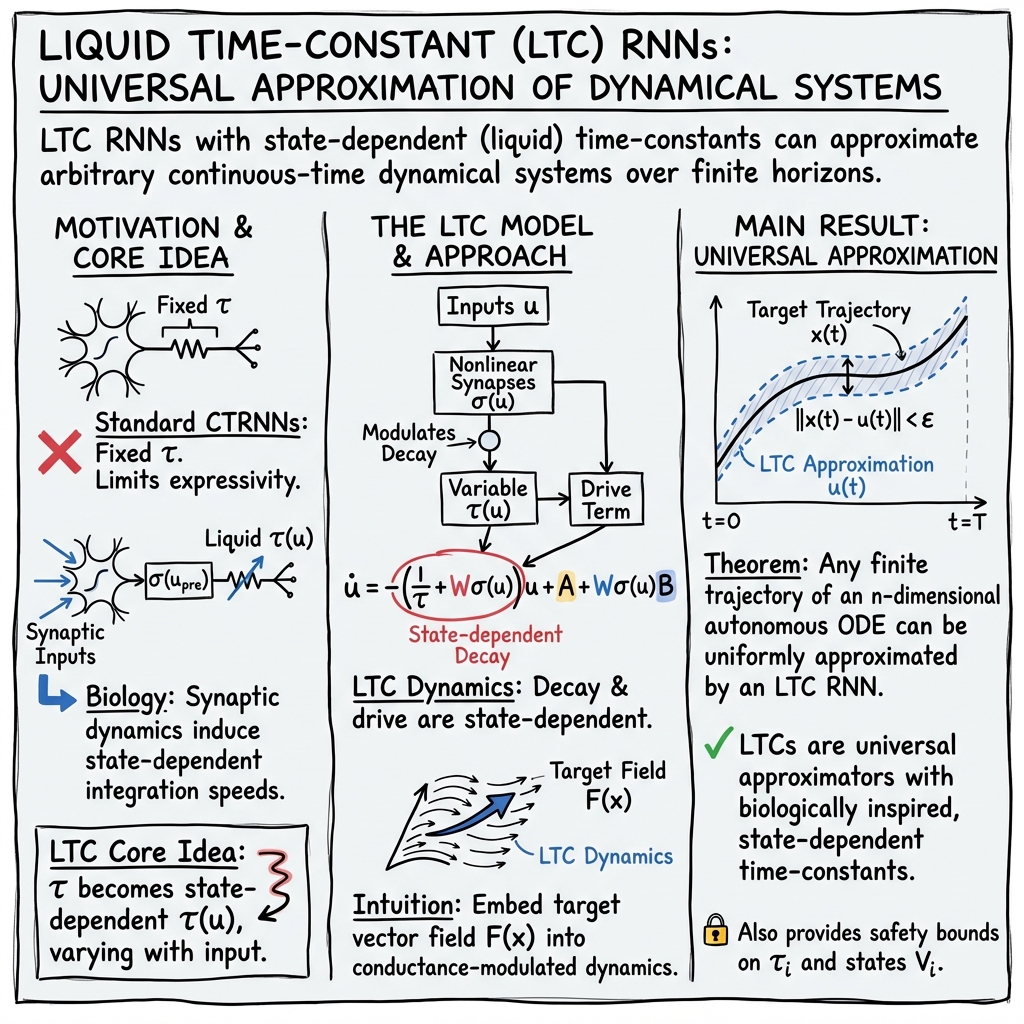
- The paper introduces Liquid Time-Constant RNNs that incorporate nonlinear synaptic dynamics to capture complex temporal behavior.
- The authors prove that LTC RNNs can approximate any finite trajectory of an n-dimensional dynamical system with arbitrarily small error.
- The study establishes explicit theoretical bounds on neuron time constants and state dynamics, ensuring stable operation in practical applications.
Liquid Time-Constant Recurrent Neural Networks as Universal Approximators
Introduction
The paper "Liquid Time-constant Recurrent Neural Networks as Universal Approximators" (1811.00321) presents a novel approach to Recurrent Neural Networks (RNNs) by introducing Liquid Time-constant (LTC) RNNs. This innovative model is inspired by biological synaptic transmission dynamics observed in certain neurological systems, such as those of Ascaris and C. elegans. This model diverges from traditional continuous-time RNNs (CTRNNs) by allowing synapses to exhibit nonlinear sigmoidal responses, which in turn create dynamic, context-dependent time constants for neuron activation. The primary contributions of this work include formalizing the LTC RNN model, proving its universal approximation capabilities, and establishing theoretical bounds on neuron time constants and states.
Liquid Time-Constant RNNs
LTC RNNs are built on the principle that the time constant of neuron dynamics can vary according to the nonlinear properties of synaptic inputs, particularly chemical synapses characterized by sigmoidal activation functions. The dynamics of neuron membrane potential in these networks are governed by a set of ordinary differential equations (ODEs) that incorporate both chemical and electrical synaptic inputs, manipulating the membrane integrator characteristics of the neuron.
The mathematical formulation presents time constants that vary dynamically, resulting in the distinctive capability to capture complex dynamics with fewer computational units than traditional methods. By doing so, it models the neuron interaction more biologically plausibly, enhancing the expressiveness and applicability of the network in various domains, including neuromorphic simulations, adaptive control systems, and reinforcement learning scenarios.
Universal Approximation Capabilities
A critical aspect of this research is the formal proof demonstrating that LTC RNNs possess universal approximation properties. Specifically, it shows that LTC RNNs can approximate any finite trajectory of an n-dimensional dynamical system. This result is significant as it extends the theoretical foundation of neural network approximators into the domain of dynamic temporal systems.
The proof leverages prior universal approximation theorems applicable to both feedforward and recurrent neural networks, adapting these principles to dynamic, continuous-time systems with variable-responsiveness neurons. The authors provide a rigorous theorem substantiating that with sufficiently many hidden units and appropriate parameterization, LTC RNNs can achieve an approximation error below any desired threshold for a given dynamic process.
Bounds on Time-Constants and Network States
The paper further explores the behavior of neuronal time constants and state dynamics within LTC RNNs, proving that both are bounded within specific ranges. The study identifies explicit boundary conditions for time constants and neuronal states, contributing to a more comprehensive understanding of the constraints and operational limits of these neural networks. Such bounds are crucial for ensuring stable and reliable operation in practical applications, particularly where real-time adaptation and prediction are necessary.
Conclusion
The introduction of Liquid Time-constant RNNs represents a substantial advancement in the modeling of continuous-time neural networks, offering a biologically inspired alternative that provides universal approximation capabilities. The development of this framework could lead to significant improvements in a variety of applications, including complex system modeling, adaptive robotics, and neuromorphic computing. Theoretical insights such as the bounded nature of time constants and state dynamics reinforce the practicality of LTC RNNs. This work lays the groundwork for future exploration into biologically plausible neural network models and their applications in AI and beyond. Future research may focus on expanding these concepts into larger-scale simulations and more diverse biological models to explore their full potential.